js ajax로 구현된 A* 게임 경로 알고리즘 컴파일

일부 소개 다시 게시 [http://data.gameres.com/message.asp?TopicID=25439에서 재인쇄]

오래 전에 A* 알고리즘에 대해 알고 있었지만 읽어본 적이 없습니다. 관련 기사를 진지하게 읽어보진 못했습니다. 코드를 읽지 않았는데 막연한 개념만 머릿속에 떠오릅니다. 이번에는 인공지능 학습의 시작으로 강력 추천하는 간단한 방법을 처음부터 다시 공부해 보기로 했습니다.
이 기사는 중국에 있는 많은 사람들이 번역했어야 하는 글인데, 번역 자체도 제 영어 실력을 위한 연습이 아닌가 싶습니다. 열심히 노력한 끝에 마침내 문서를 완성하고 A* 알고리즘의 원리를 이해했습니다. 저자가 이 마법의 알고리즘을 단순한 것부터 심오한 것까지 생생한 설명과 간결하고 유머러스한 언어로 설명한다는 것은 의심의 여지가 없습니다. 나는 이 책을 읽는 모든 사람이 어느 정도 이해할 것이라고 믿습니다. -비).
원본 링크: http://www.gamedev.net/reference/articles/article2003.asp

다음은 번역된 내용입니다. (편집은 울트라에디트를 사용하기 때문에 원문의 각종 링크(차트 제외)는 처리하지 않았습니다. 이는 무단 링크 의혹을 피하기 위함이기도 합니다. 관심 있는 독자들은 원문을 참고하시기 바랍니다.

참가자도 어렵지 않습니다. A*(A스타로 발음) 알고리즘은 초보자에게 정말 어렵습니다.

이 글은 이 주제에 대해 권위 있는 진술을 하려는 것이 아니라, 알고리즘의 원리만 설명합니다. .

마지막으로 이 기사에는 원하는 대로 모든 컴퓨터 프로그래밍 언어로 구현할 수 있습니다. 압축된 패키지에는 C 및 Blitz Basic 언어 버전이 포함되어 있습니다. 실행 파일도 포함되어 있습니다.

순서. : 검색 영역

아래와 같이 A지점에서 B지점으로 이동하려고 한다고 가정해 보겠습니다. 녹색이 시작점 A, 빨간색이 끝점 B, 파란색 사각형이 됩니다.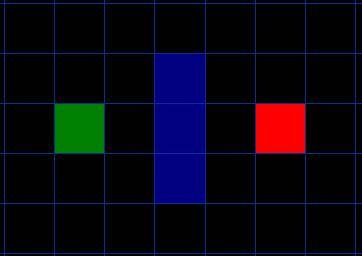




가장 먼저 눈에 띄는 것은 검색 영역이 이렇게 사각형 격자로 나뉘어져 있다는 점입니다. 이 방법은 검색 영역을 2차원 배열로 단순화합니다. 배열의 각 요소는 그리드의 정사각형이며 정사각형은 A에서 통과할 수 있는 경로로 표시됩니다. B. 일단 경로를 찾으면 우리 사람은 목적지에 도달할 때까지 한 사각형의 중심에서 다른 사각형으로 걸어갑니다. 이러한 중간 지점을 "노드"라고 합니다. 경로가 정사각형이 아닌 다른 구조로 분할될 수 있기 때문에 직사각형, 육각형 또는 기타 모양이 될 수 있습니다. 노드는 중앙이나 모서리를 따라 배치될 수 있습니다. 이 시스템을 그대로 사용합니다.

검색 시작

위의 그리드에서 했던 것처럼 검색 영역이 다루기 쉬운 노드로 변환됩니다. , 다음 단계는 최단 경로를 찾기 위해 검색을 안내하는 것입니다. A* 경로 찾기 알고리즘에서는 A 지점에서 시작하여 인접한 사각형을 확인하고 대상을 찾을 때까지 바깥쪽으로 확장합니다. :

.
1. A 지점부터 시작하여 보류 지점으로 저장합니다. 지금은 목록에 항목이 하나만 있지만 더 많은 항목이 있습니다. 경로는 포함된 사각형을 통과할 수도 있고 그렇지 않을 수도 있습니다. 기본적으로 이것은 확인할 사각형의 목록입니다.
2. 벽을 건너뛰고 시작점 주변에서 도달할 수 있거나 통과할 수 있는 모든 사각형을 찾습니다. , 물 또는 통과할 수 없는 지형의 기타 블록. 또한 공개 목록에 추가하십시오. 점 A를 이 모든 사각형의 "상위 사각형"으로 저장합니다. 경로를 설명하려면 상위 사각형의 정보가 매우 중요합니다. 구체적인 용도는 나중에 설명하겠습니다.
3. 열린 목록에서 A 지점을 삭제하고 다시 확인할 필요가 없는 모든 사각형을 저장하는 "닫힌 목록"에 추가합니다.

이때 사진과 같은 구조가 되어야 합니다. 그림에서 진한 녹색 사각형이 시작 사각형의 중심입니다. 연한 파란색 윤곽선으로 표시되어 닫기 목록에 추가되었음을 나타냅니다. 이제 인접한 모든 셀이 열린 목록에 있으며 연한 녹색 윤곽선으로 표시됩니다. 각 사각형에는 시작 사각형인 상위 사각형을 가리키는 회색 포인터가 있습니다.





다음으로 목록에서 인접한 사각형을 열도록 선택하고 다음과 같이 이전 프로세스를 대략적으로 반복합니다. 그런데 우리는 어떤 사각형을 선택해야 할까요? F 값이 가장 낮은 것입니다.

경로 점수
경로에서 통과할 사각형을 선택하는 열쇠는 다음 방정식입니다.

F = G H

여기:
* G = 생성된 경로를 따라 시작점 A에서 그리드의 지정된 사각형까지 이동하는 비용입니다.
* H = 그리드의 해당 사각형에서 끝점 B까지 이동하는 데 드는 예상 이동 비용입니다. 이것을 종종 휴리스틱(heuristic)이라고 부르는데, 이는 약간 혼란스러울 수 있습니다. 그렇게 불리는 이유는 단지 추측일 뿐이기 때문입니다. 도중에 다양한 장애물(벽, 물 등)이 있을 수 있으므로 경로의 길이를 미리 알 수 있는 방법이 없습니다. 이 문서에서는 H를 계산하는 한 가지 방법만 제공하지만 온라인에서 다른 많은 방법을 찾을 수 있습니다.

우리의 경로는 열린 목록을 반복적으로 탐색하고 F 값이 가장 낮은 사각형을 선택하여 생성됩니다. 이 기사에서는 이 프로세스를 더 자세히 설명합니다. 먼저, 이 방정식을 계산하는 방법을 자세히 살펴보겠습니다.

위에서 언급했듯이 G는 시작점에서 현재점까지의 경로를 따라 이동하는 비용을 나타냅니다. 이 예에서는 수평 또는 수직 이동 비용을 10으로, 대각선 비용을 14로 설정했습니다. 대각선을 따른 거리는 2의 제곱근(두려워하지 마세요), 즉 수평 또는 수직 이동 비용의 약 1.414배이기 때문에 이러한 값을 사용합니다. 단순화를 위해 근사치로 10과 14를 사용합니다. 비율은 대부분 정확하며 근연산과 소수점은 사용하지 않습니다. 단지 문제가 두렵거나 수학을 좋아하지 않기 때문만은 아닙니다. 이와 같은 정수를 사용하는 것이 컴퓨터에서도 더 빠릅니다. 이러한 단순화를 사용하지 않으면 길 찾기 속도가 매우 느려진다는 사실을 곧 알게 될 것입니다.

특정 경로를 따라 특정 사각형으로 이어지는 G 값을 계산하므로 평가 방법은 상위 노드의 G 값을 가져온 다음 대각선인지 직각 상대인지 판단하는 것입니다. (대각선 밖에서) 각각 14와 10씩 증가합니다. 이 방법은 시작 사각형에서 두 개 이상의 사각형을 얻기 때문에 예제에서 더 까다로워집니다.

H값은 다양한 방법으로 추정할 수 있습니다. 여기서 사용하는 방법을 맨하탄법(Manhattan Method)이라고 하는데, 대각선 방향을 무시하고 현재 정사각형부터 대상 정사각형까지 가로, 세로 정사각형의 개수를 합산하는 방식이다. 그런 다음 결과에 10을 곱합니다. 대각선으로 블록을 가로질러 갈 수 없는 도시에서 한 장소에서 다른 장소까지의 블록 수를 세는 것과 비슷하다고 해서 이것을 맨해튼 방식이라고 합니다. 모든 장애물을 무시하는 것이 매우 중요합니다. 이는 실제 값이 아닌 남은 거리에 대한 추정치이므로 이 방법을 휴리스틱(heuristic)이라고 합니다. 더 알고 싶으십니까? 여기에서 방정식과 추가 참고 사항을 찾을 수 있습니다.

F값은 G와 H의 합입니다. 첫 번째 검색 단계의 결과는 아래 차트에서 확인할 수 있습니다. 각 상자에는 F, G, H 등급이 적혀 있습니다. 시작 사각형의 바로 오른쪽에 있는 사각형으로 표시된 대로 F는 왼쪽 상단 모서리에, G는 왼쪽 하단 모서리에, H는 오른쪽 하단 모서리에 인쇄됩니다.



이제 사각형을 살펴보겠습니다. 문자 사각형에서 G = 10입니다. 이는 시작 셀에서 가로 방향으로 한 칸만 떨어져 있기 때문입니다. 시작 사각형의 바로 위, 아래, 왼쪽에 있는 사각형의 G 값은 모두 10입니다. 대각선 방향의 G 값은 14입니다.

가로와 세로 방향으로만 이동하고 중간 벽을 무시하는 빨간색 타겟 그리드까지의 맨해튼 거리를 풀어 H 값을 구합니다. 이 방법을 사용하면 시작점 바로 오른쪽에 있는 사각형은 빨간색 사각형에서 3칸 떨어져 있고 H 값은 30입니다. 이 사각형 위의 사각형은 4칸 떨어져 있으며(수평 및 수직으로만 이동할 수 있음을 기억하세요) H 값은 40입니다. 다른 사각형의 H 값을 계산하는 방법을 대략적으로 알아야 합니다~.

각 그리드의 F 값은 여전히 ​​단순히 G와 H의 합입니다.

검색 계속

검색을 계속하려면 다음에서 F를 선택하면 됩니다. 목록 열기 가장 낮은 값을 갖는 사각형입니다. 그런 다음 선택한 사각형에 대해 다음 처리를 수행합니다.

4. 열린 목록에서 삭제한 다음 닫힌 목록에 추가합니다.
5. 인접한 그리드를 모두 확인하세요. 이미 닫힌 목록에 있거나 통과할 수 없는 항목(벽, 물 또는 기타 통과할 수 없는 지형이 있는 지형)을 건너뛰고 아직 해당 목록에 없으면 공개 목록에 추가하세요. 선택한 사각형을 새 사각형의 상위 노드로 만듭니다.
6. 인접한 그리드가 이미 열려 있는 목록에 있는 경우 현재 경로가 더 나은지 확인하세요. 즉, 새 경로를 사용하여 G 값에 도달하면 G 값이 더 낮아지는지 확인하세요. 그렇지 않다면 아무것도 하지 마십시오.
반면, 새 G 값이 더 낮으면 인접한 사각형의 상위 노드를 현재 선택된 사각형으로 변경합니다(위 다이어그램에서는 화살표 방향을 이 사각형을 가리키도록 변경). 마지막으로 F와 G의 값을 다시 계산합니다. 이것이 충분히 명확하지 않은 경우 아래 다이어그램을 볼 수 있습니다.

자, 어떻게 작동하는지 살펴보겠습니다. 원래 9개의 정사각형 그리드 중 시작점이 닫힌 목록으로 전환된 후 열린 목록에는 8개가 남았습니다. 그 중 F값이 가장 낮은 것이 출발 그리드 바로 오른쪽 그리드이며, F값은 40이다. 따라서 우리는 이 사각형을 처리할 다음 사각형으로 선택합니다. 다음 그림에서는 파란색으로 강조 표시되어 있습니다.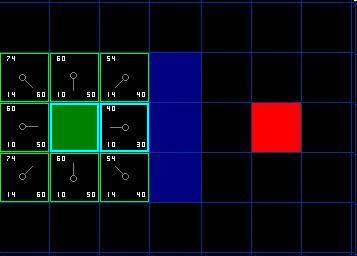




먼저 공개 목록에서 꺼내서 비공개 목록에 넣습니다(그래서 파란색으로 강조 표시되어 있습니다). 그런 다음 인접한 셀을 확인합니다. 아, 오른쪽 그리드는 벽이니까 건너뛰겠습니다. 왼쪽 그리드가 시작 그리드입니다. 닫기 목록에 있으므로 생략합니다.

다른 4개의 사각형은 이미 열려 있는 목록에 있으므로 G 값을 확인하여 이 사각형을 통과하면 경로가 더 나은지 결정합니다. 선택한 그리드 아래의 사각형을 살펴보겠습니다. G 값은 14입니다. 현재 사각형에서 그곳으로 이동하면 G값은 20이 됩니다(현재 사각형에 도달하는 G값은 10이고 위쪽 사각형으로 이동하면 G값이 10만큼 증가합니다). G 값 20이 14보다 크기 때문에 이 방법은 더 나은 경로가 아닙니다. 사진을 보시면 이해가 되실 겁니다. 정사각형 하나를 수평으로 이동한 다음 수직으로 하나 이동하는 대신 대각선으로 하나의 정사각형을 이동하는 것이 더 쉬울 것입니다.

이미 열려 있는 목록에 있는 4개의 인접 셀에 대해 이 과정을 반복하면 현재 셀을 사용하여 경로를 개선할 수 없다는 것을 알게 되므로 변경하지 않습니다. 이제 인접한 셀을 모두 확인했으므로 다음 셀로 이동할 수 있습니다.

그래서 우리는 공개 목록을 검색합니다. 이제 그 안에는 7개의 셀만 있습니다. 여전히 F 값이 가장 낮은 셀을 선택합니다. 흥미로운 점은 이번에는 두 그리드의 값이 54라는 것입니다. 우리는 어떻게 선택합니까? 그것은 번거롭지 않습니다. 속도면에서는 목록에 추가된 마지막 그리드를 선택하는 것이 더 빠릅니다. 이로 인해 길찾기 과정에서 목표에 접근할 때 새로 발견된 그리드를 먼저 사용하는 것이 선호됩니다. 그러나 그것은 중요하지 않습니다. (동일한 값을 다르게 처리하면 동일한 길이의 서로 다른 경로를 찾는 A* 알고리즘의 서로 다른 버전이 발생합니다.)

그런 다음 그림과 같이 시작 그리드의 오른쪽 하단에 있는 그리드를 선택합니다. 수치.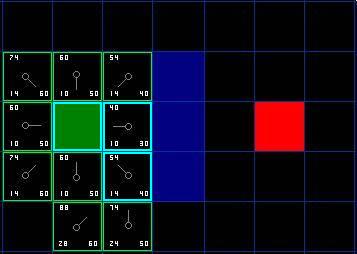




이번에 인접한 그리드를 확인해보니 오른쪽에 벽이 있는 것을 발견하여 건너뛰었습니다. 상단 상자도 건너뜁니다. 또한 벽 아래의 그리드도 건너뛰었습니다. 왜? 모퉁이를 통하지 않고는 그 광장에 직접 도달할 수 없기 때문입니다. 먼저 아래로 내려간 다음 해당 블록에 도달하고 해당 모퉁이를 단계별로 통과해야 합니다. (참고: 모서리를 교차하는 규칙은 선택 사항입니다. 노드 배치 방법에 따라 다릅니다.)

그러면 나머지 5개의 사각형이 남습니다. 현재 셀 아래의 다른 두 셀은 현재 열린 목록에 없으므로 이를 추가하고 현재 셀을 상위 노드로 지정합니다. 나머지 3개의 사각형 중 2개는 이미 열려 있는 목록에 있으므로(시작 사각형과 현재 사각형 위의 사각형은 표에서 파란색으로 강조 표시됨) 이를 건너뜁니다. 현재 사각형의 왼쪽에 있는 마지막 사각형을 확인하여 이 경로를 통해 G 값이 더 낮은지 확인합니다. 걱정하지 마십시오. 열려 있는 목록에서 다음 상자를 확인할 준비가 되었습니다.

아래 이미지와 같이 대상 셀이 열린 목록에 추가될 때까지 이 과정을 반복합니다.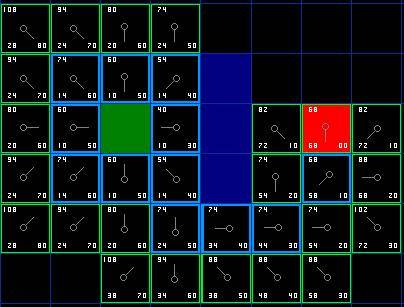




시작 그리드 아래 그리드의 상위 노드가 이전 그리드와 다르다는 점에 유의하세요. 이전에는 G 값이 28이었고 오른쪽 위 그리드를 가리켰습니다. G 값은 이제 20이며 그 위의 사각형을 가리킵니다. 이는 경로 찾기 프로세스의 어딘가에서 발생하며, 새 경로가 적용될 때 G 값이 확인되어 낮아집니다. 따라서 상위 노드가 다시 할당되고 G 및 F 값이 다시 계산됩니다. 이 예에서는 이 변경 사항이 중요하지 않지만 많은 경우 이 변경으로 인해 경로 찾기 결과가 크게 변경될 수 있습니다.

그럼 이 경로는 어떻게 결정하나요? 매우 간단합니다. 빨간색 대상 그리드에서 시작하여 화살표 방향으로 상위 노드를 향해 이동합니다. 이것은 결국 당신을 시작 광장으로 다시 데려다줄 것이며, 그것이 당신의 길입니다! 그림과 같아야 합니다. 시작 그리드 A에서 목표 그리드 B로 이동하는 것은 단순히 각 그리드(노드)의 중간점에서 다음 그리드까지 경로를 따라 목표 지점에 도달할 때까지 이동하면 되는 문제입니다. 그렇게 간단합니다.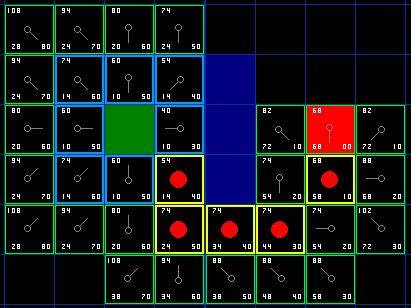





A* 메소드 요약

자, 이제 전체 설명을 읽었으므로 각 단계를 적어 보겠습니다. Together에서의 동작:

1. 열린 목록에 시작 그리드를 추가합니다.
2. 다음 작업을 반복합니다.
a) 열린 목록에서 F 값이 가장 낮은 그리드를 찾습니다. 우리는 그것을 현재 그리드라고 부릅니다.
b) 목록을 닫으려면 전환하세요.
c) 8개의 인접한 셀 각각에 대해?
* 통과할 수 없거나 이미 비공개 목록에 있는 경우 건너뛰세요. 그 반대는 다음과 같습니다.
* 공개목록에 없으면 추가해주세요. 현재 그리드를 이 그리드의 상위 노드로 만듭니다. 이 그리드의 F, G, H 값을 기록합니다.
* 이미 열려 있는 목록에 있는 경우 G 값을 참조로 사용하여 새 경로가 더 나은지 확인하세요. G가 낮을수록 더 나은 경로를 의미합니다. 그렇다면 이 셀의 부모 노드를 현재 셀로 변경하고, 이 셀의 G, F 값을 다시 계산합니다. 열린 목록을 F 값으로 정렬한 상태로 유지하는 경우 열린 목록을 변경한 후 다시 정렬해야 할 수도 있습니다.

D) 중지합니다. *개시 목록에 대상 그리드를 추가하면 이때 경로가 발견되거나
*대상 그리드가 발견되지 않고 목록이 비어 있습니다. 현재는 해당 경로가 존재하지 않습니다.
3. 경로를 저장합니다. 대상 셀에서 시작하여 시작 셀로 돌아갈 때까지 각 셀의 부모 노드를 따라 이동합니다. 이것이 당신의 길입니다.

여담

주제에서 벗어났네요 죄송합니다만 인터넷이나 관련 포럼에서 A*에 대한 다양한 토론을 보면 가끔 실제로는 그렇지 않지만 A* 알고리즘에 대한 코드입니다. A*를 사용하려면 위에서 설명한 모든 요소(특정 열기 및 닫기 목록)를 포함해야 하며 경로 평가에 F, G 및 H를 사용해야 합니다. 다른 많은 길 찾기 알고리즘이 있지만 그 중 최고로 간주되는 A*는 아닙니다. Bryan Stout는 이 기사의 뒷부분에 나오는 참조 문서에서 장점과 단점을 포함하여 그 중 일부에 대해 논의합니다. 때로는 특정 상황에서 다른 알고리즘이 더 나을 수도 있지만, 자신이 무엇을 하고 있는지 정확히 알아야 합니다. 알았어, 그거면 충분해. 기사로 돌아갑니다.

구현 참고 사항

이제 기본 원칙을 이해했으므로 프로그램 작성 시 고려해야 할 몇 가지 추가 사항이 있습니다. 아래 자료 중 일부는 제가 C와 Blitz Basic으로 작성한 프로그램을 참조하지만, 다른 언어로 작성된 코드도 똑같이 유효합니다.

1. 공개 목록 유지: 이는 A* 경로 찾기 알고리즘의 가장 중요한 구성 요소입니다. 열린 목록에 접근할 때마다 F 값이 가장 낮은 사각형을 찾아야 합니다. 이를 수행하는 방법에는 몇 가지가 있습니다. 경로 요소를 마음대로 저장할 수 있으며, F 값이 가장 낮은 요소를 찾아야 할 경우 열린 목록을 순회합니다. 이는 간단하지만 특히 긴 경로의 경우 너무 느립니다. 이는 정렬된 셀 목록을 유지함으로써 개선될 수 있습니다. F 값이 가장 낮은 셀을 찾을 때마다 목록의 첫 번째 요소만 선택하면 됩니다. 이 접근 방식은 직접 구현할 때 첫 번째 선택입니다.

미니맵에서. 이 방법은 효과적이지만 가장 빠른 솔루션은 아닙니다. 속도를 더욱 요구하는 A* 프로그래머들은 "바이너리 힙"이라는 방법을 사용하는데, 이는 제가 코드에서 사용하는 방법이기도 합니다. 내 경험에 따르면 이 방법은 대부분의 상황에서 2~3배 더 빠르며, 긴 경로에서는 속도가 기하급수적으로(10배 이상) 증가합니다. 바이너리 힙에 대해 자세히 알아보려면 내 기사 A* Pathfinding에서 바이너리 힙 사용을 확인하세요.

2. 기타 단위: 제 예제 코드를 보면 다른 단위를 완전히 무시한다는 것을 알 수 있습니다. 내 길 찾기는 실제로 서로를 통해 이동할 수 있습니다. 특정 게임에 따라 이것이 작동할 수도 있고 작동하지 않을 수도 있습니다. 서로 우회할 수 있다는 희망으로 다른 유닛을 고려하려는 경우 경로 찾기 알고리즘에서 다른 유닛을 무시하고 충돌 감지를 위한 새로운 코드를 작성하는 것이 좋습니다. 충돌이 발생하면 도중에 장애물이 없을 때까지 새 경로를 생성하거나 일부 표준 이동 규칙(예: 항상 오른쪽 등)을 사용한 다음 새 경로를 생성할 수 있습니다. 초기 경로 계산에서 다른 유닛은 고려되지 않는 이유는 무엇입니까? 왜냐하면 다른 유닛이 이동하고 원래 위치에 도착할 때쯤에는 유닛이 떠났을 수도 있기 때문입니다. 이로 인해 유닛이 더 이상 존재하지 않는 유닛을 피하기 위해 방향을 바꾸거나, 경로를 계산한 후 해당 경로로 돌진하는 유닛과 부딪히는 이상한 결과가 발생할 수 있습니다.

그러나 길 찾기 알고리즘에서 다른 객체를 무시한다는 것은 별도의 충돌 감지 코드를 작성해야 한다는 것을 의미합니다. 이는 게임마다 다르므로 결정은 귀하에게 맡기겠습니다. 참조 목록에서 Bryan Stout의 기사에는 몇 가지 가능한 솔루션(예: 강력한 추적 등)이 있으므로 살펴볼 가치가 있습니다.

3. 몇 가지 속도 팁: 자신만의 A* 프로그램을 개발하거나 프로그램을 다시 작성할 때 특히 개체가 많은 대규모 지도에서 경로 찾기에 많은 CPU 시간이 소요된다는 것을 알게 될 것입니다. 당신의 방식. 인터넷에서 다른 자료를 읽어보면 스타크래프트나 에이지 오브 엠파이어를 개발한 전문가라도 어쩔 수 없다는 것을 이해하게 될 것이다. 길 찾기가 너무 느리다고 생각되면 도움이 될 수 있는 몇 가지 제안 사항이 있습니다.

* 더 작은 지도나 더 적은 수의 길 찾기를 사용하세요.
* 동시에 여러 개체의 경로를 찾지 마세요. 대신 대기열에 추가하고 여러 게임 주기에 걸쳐 경로 찾기 프로세스를 분산시키세요. 게임이 초당 40사이클로 실행된다면 아무도 눈치 채지 못할 것입니다. 그러나 많은 수의 길잡이가 경로를 계산하면 게임 속도가 갑자기 느려지는 것을 알게 될 것입니다.
* 더 큰 지도 그리드를 사용해 보세요. 이렇게 하면 길 찾기에서 검색되는 총 그리드 수가 줄어듭니다. 야망이 있다면 경로 길이에 따라 서로 다른 상황에서 사용할 수 있는 두 개 이상의 경로 찾기 시스템을 설계할 수 있습니다. 이것이 바로 전문가들이 하는 일입니다. 넓은 영역을 사용하여 긴 경로를 계산한 다음, 대상에 가까워지면 작은 그리드/영역을 사용하여 세분화된 경로 찾기로 전환합니다. 이 아이디어에 관심이 있다면 내 기사 Two-Tiered A* Pathfinding을 확인하세요.
* 웨이포인트 시스템을 사용하여 긴 경로를 계산하거나 경로를 미리 계산하여 게임에 추가하세요.
* 지도의 어떤 영역에 접근할 수 없는지 나타내기 위해 지도를 사전 처리합니다. 나는 이 지역을 '섬'이라고 부릅니다. 실제로는 섬일 수도 있고 벽으로 둘러싸인 기타 접근하기 어려운 지역일 수도 있습니다. A*의 하한은 해당 지역에 대한 경로를 찾으라고 지시할 때 목록을 열고 닫아 도달 가능한 모든 사각형/노드가 계산될 때까지 전체 지도를 검색한다는 것입니다. 이로 인해 CPU 시간이 많이 낭비됩니다. 이는 이러한 영역을 미리 결정하고(예: 홍수 채우기 또는 유사한 방법을 통해) 이 정보를 일종의 배열에 기록하고 경로 찾기를 시작하기 전에 확인함으로써 피할 수 있습니다. 내 Blitz 버전의 코드에서는 이 작업을 수행하기 위해 지도 전처리기를 구축했습니다. 또한 길찾기 알고리즘이 무시할 수 있는 막다른 골목을 표시하여 길찾기 속도를 더욱 높입니다.

4. 다양한 지형 손실: 이 튜토리얼과 제가 첨부한 프로그램에는 통행 가능한 지형과 통행 불가능한 지형의 두 가지 유형만 있습니다. 그러나 횡단이 가능하지만 이동하는 데 비용이 더 많이 드는 지형(늪, 언덕, 던전 계단 등)이 필요할 수 있습니다. 이곳은 횡단이 가능한 지형이지만 평평한 개방형 지역보다 이동 비용이 더 많이 듭니다. 마찬가지로 도로는 자연 지형보다 이동 비용이 저렴해야 합니다.

이 문제는 모든 지형의 G 값을 계산할 때 지형 손실을 추가하면 쉽게 해결됩니다. 여기에 추가 손실을 추가하기만 하면 됩니다. A* 알고리즘은 가장 낮은 비용으로 경로를 찾도록 설계되었기 때문에 이러한 상황을 쉽게 처리할 수 있습니다. 제가 제공한 간단한 예에는 통과 가능 및 통과 불가능이라는 두 가지 유형의 지형만 있습니다. A*는 가장 짧고 가장 직접적인 경로를 찾습니다. 그러나 지형 비용이 다양한 경우 가장 저렴한 경로는 늪을 직접 통과하지 않고 주변 경로를 따라가는 것과 같이 장거리 이동을 포함할 수 있습니다.

추가적인 고려가 필요한 상황 중 하나는 전문가들이 '영향 매핑'(가칭: 영향력 매핑)이라고 부르는 것입니다. 위에서 설명한 다양한 지형 비용과 마찬가지로 추가 포인트 시스템을 만들어 길찾기 AI에 적용할 수 있습니다. 많은 수의 길잡이가 있는 지도가 있고 그들 모두가 산악 지역을 통과하고 있다고 가정해 보십시오. 컴퓨터가 해당 패스를 통해 경로를 생성할 때마다 더 혼잡해집니다. 원하는 경우 대량 학살 이벤트로 헥스에 부정적인 영향을 미치는 영향 지도를 생성할 수 있습니다. 이렇게 하면 컴퓨터가 더 안전한 경로를 선호하게 되고 단순히 길이가 더 짧다는 이유(그러나 잠재적으로 더 위험할 수 있음) 때문에 파티와 길잡이를 특정 경로로 지속적으로 보내는 것을 방지하는 데 도움이 됩니다.

5. 알 수 없는 지역 다루기: 아직 지도를 탐색하지 않았더라도 컴퓨터가 항상 어느 경로가 올바른지 아는 PC 게임을 플레이해 본 적이 있나요? 게임의 경우 너무 좋은 길 찾기는 비현실적으로 보일 수 있습니다. 다행히도 이는 쉽게 해결할 수 있는 문제입니다.

답은 각기 다른 플레이어와 컴퓨터(플레이어당, 유닛당이 아닌 - 많은 메모리를 소비함)에 대해 별도의 "knownWalkability" 배열을 만드는 것입니다. 각 배열에는 탐색한 플레이어 영역이 포함되어 있습니다. 그리고 달리 입증될 때까지 통과 가능한 것으로 간주되는 기타 영역. 이 접근 방식을 사용하면 부대는 길의 막다른 골목에 머물며 길을 찾을 때까지 잘못된 선택을 하게 됩니다. 지도를 탐색한 후에는 길찾기가 평소대로 진행됩니다.

6. 부드러운 경로: A*는 가장 짧고 비용이 저렴한 경로를 제공하지만 자동으로 매끄러운 경로를 제공할 수는 없습니다. 예제의 결과 경로를 살펴보십시오(그림 7). 첫 번째 단계는 시작 그리드의 오른쪽 아래에 있습니다. 이 단계가 직접 아래쪽에 있었다면 경로가 더 매끄러워지지 않았을까요?

이 문제를 해결하는 방법에는 여러 가지가 있습니다. 경로를 계산할 때 G 값에 추가 값을 추가하면 그리드 방향에 부정적인 영향을 줄 수 있습니다. 또는 경로가 계산된 후 경로를 따라 달리고 인접한 사각형을 바꾸면 경로가 더 부드러워 보일 수 있는 위치를 찾을 수 있습니다. 전체 결과를 보려면 Gamasutra.com에서 Marco Pinter가 작성한 기사(무료이지만 등록이 필요함)인 Toward More Realistic Pathfinding을 확인하세요.

7. 비정사각형 검색 영역: 우리의 경우 간단한 2D를 사용합니다. 정사각형 플롯. 이 방법을 사용할 필요는 없습니다. 불규칙한 모양의 영역을 사용할 수 있습니다. Adventure Chess 게임과 그 게임에 등장하는 국가를 생각해 보세요. 그런 길 찾기 수준을 디자인할 수 있습니다. 이렇게 하려면 인접 국가 테이블과 한 국가에서 다른 국가로 이동하기 위한 G 값을 만들어야 할 수도 있습니다. 또한 H 값을 추정하는 방법이 필요합니다. 다른 모든 것은 예제와 정확히 동일합니다. 열려 있는 목록에 새 요소를 추가해야 하는 경우 인접한 셀을 사용할 필요가 없으며 대신 테이블에서 인접한 국가를 찾으십시오.

마찬가지로, 정의된 지형 지도에 대한 웨이포인트 시스템을 생성할 수 있습니다. 웨이포인트는 일반적으로 도로나 던전 통로의 전환점입니다. 게임 디자이너는 이러한 웨이포인트를 미리 설정할 수 있습니다. 두 웨이포인트 사이의 직선에 장애물이 없으면 두 웨이포인트는 인접한 것으로 간주됩니다. Adventure Chess 예에서는 이 인접 정보를 테이블에 저장하고 열려 있는 목록에 요소를 추가해야 할 때 사용할 수 있습니다. 그런 다음 관련 G 값(두 지점 사이의 직선 거리 사용 가능), H 값(대상 지점까지의 직선 거리 사용 가능)을 기록하고 나머지는 이전과 같이 수행하면 됩니다.

정사각형이 아닌 영역에서 RPG 지도를 검색하는 또 다른 예를 보려면 내 기사 Two-Tiered A* Pathfinding을 확인하세요.

추가 읽기

자, 이제 몇 가지 추가 사항에 대해 사전 이해가 되었습니다. 이 시점에서는 내 소스 코드를 공부하는 것이 좋습니다. 패키지에는 C로 작성된 버전과 Blitz Basic으로 작성된 두 가지 버전이 포함되어 있습니다. 그건 그렇고, 두 버전 모두 주석이 잘 되어 있고 읽기 쉽습니다. 여기에 링크가 있습니다.

* 예시 코드: A* Pathfinder(2D) 버전 1.71

C나 Blitz Basic을 모두 사용하지 않는 경우 C 버전에는 두 개의 작은 실행 파일이 있습니다. Blitz Basic은 Blitz Basic 웹사이트에서 무료로 다운로드할 수 있는 Blitz Basic 3D 데모 버전(Blitz Plus 아님)에서 실행할 수 있습니다. Ben O'Neill이 제공하는 온라인 데모는 여기에서 찾을 수 있습니다.

다음 웹페이지도 살펴보세요. 이 튜토리얼을 읽고 나면 이해하기가 훨씬 쉬워질 것입니다.

* Amit의 A* 페이지: Amit Patel이 제작한 널리 인용되는 페이지로, 이 기사를 미리 읽지 않았다면 이해하기 어려울 수 있습니다. 볼만한 가치가 있습니다. 특히 이 문제에 대한 Amit의 견해는 더욱 그렇습니다.
* 스마트한 움직임: 지능형 경로 찾기: Bryan Stout가 Gamasutra.com에 게시한 이 기사를 읽으려면 등록이 필요합니다. 등록은 무료이며 이 기사 및 사이트의 다른 리소스에 비해 가격 대비 가치가 높습니다. Bryan이 Delphi에서 작성한 프로그램은 A*를 배우는 데 도움이 되었으며 A* 코드에 대한 영감의 원천이었습니다. 또한 A*의 여러 변형에 대해서도 설명합니다.
* 지형 분석: Ensemble Studios의 전문가인 Dave Pottinge가 작성한 고급이지만 재미있는 주제입니다. 이 사람은 Age of Empires와 Age of Kings의 개발에 참여했습니다. 여기에 있는 내용을 모두 이해할 것이라고 기대하지는 마세요. 하지만 여러분만의 아이디어를 줄 수 있는 흥미로운 기사입니다. 여기에는 밉 매핑, 영향력 매핑 및 기타 고급 AI/경로 찾기 관점에 대한 통찰력이 포함되어 있습니다. "홍수 채우기"에 대한 논의는 내 코드의 Blitz 버전에 포함된 코드의 "막다른 골목"과 "섬"에 대한 영감을 주었습니다.

확인할 만한 다른 사이트:

* aiGuru: Pathfinding
* 게임 AI 리소스: Pathfinding
* GameDev.net: Pathfinding

알겠습니다. 모두. 혹시 이러한 아이디어를 사용하는 프로그램을 작성하신다면 이에 대해 듣고 싶습니다. 다음과 같이 연락하실 수 있습니다.
자, 행운을 빕니다!

51js에서 hjjboy 친구의 js 구현 방법을 찾았습니다. 나중에 캡슐화를 용이하게 하기 위해 주석을 추가했습니다.

코드는 다음과 같습니다.

<html><head><title>use A* to find path...</title></head> 
<body style="margin:0px"> 
<script> 
/* 
written by hjjboy 
email:tianmashuangyi@163.com 
qq:156809986 
*/ 
var closelist=new Array(),openlist=new Array();//closelist保存最终结果。openlist保存临时生成的点； 
var gw=10,gh=10,gwh=14;//参数 gh是水平附加参数 gwh是四角的附加参数。 
var p_start=new Array(2),p_end=new Array(2);//p_start为起点，p_end为终点 
var s_path,n_path="";//s_path为当前点 n_path为障碍物数组样式的字符串. 
var num,bg,flag=0; 
var w=30,h=20; 
function GetRound(pos){//返回原点周围的8个点 
    var a=new Array(); 
    a[0]=(pos[0]+1)+","+(pos[1]-1); 
    a[1]=(pos[0]+1)+","+pos[1]; 
    a[2]=(pos[0]+1)+","+(pos[1]+1); 
    a[3]=pos[0]+","+(pos[1]+1); 
    a[4]=(pos[0]-1)+","+(pos[1]+1); 
    a[5]=(pos[0]-1)+","+pos[1]; 
    a[6]=(pos[0]-1)+","+(pos[1]-1); 
    a[7]=pos[0]+","+(pos[1]-1); 
    return a; 
} 
function GetF(arr){ //参数为原点周围的8个点 
    var t,G,H,F;//F,综合的距离值，H,距离值 G,水平\角落附加计算 
    for(var i=0;i<arr.length;i++){ 
        t=arr[i].split(","); 
        t[0]=parseInt(t[0]); 
        t[1]=parseInt(t[1]); 
        if(IsOutScreen([t[0],t[1]])||IsPass(arr[i])||InClose([t[0],t[1]])||IsStart([t[0],t[1]])||!IsInTurn([t[0],t[1]])) 
            continue;//如果上面条件有一满足，则跳过本次循环，进行下一次。 
        if((t[0]-s_path[3][0])*(t[1]-s_path[3][1])!=0)//判断该点是否处于起点的垂直或横向位置上 
            G=s_path[1]+gwh;//如果不在G=14; 
        else 
            G=s_path[1]+gw;//如果在G=10; 
        if(InOpen([t[0],t[1]])){//如果当前点已存在openlist数组中 
            if(G<openlist[num][1]){ 
            maptt.rows[openlist[num][4][1]].cells[openlist[num][4][0]].style.backgroundColor="blue";//调试 
                openlist[num][0]=(G+openlist[num][2]); 
                openlist[num][1]=G; 
                openlist[num][4]=s_path[3]; 
            } 
            else{G=openlist[num][1];} 
        } 
        else{ 
            H=(Math.abs(p_end[0]-t[0])+Math.abs(p_end[1]-t[1]))*gw; 
            F=G+H; 
            arr[i]=new Array(); 
            arr[i][0]=F; 
            arr[i][1]=G; 
            arr[i][2]=H; 
            arr[i][3]=[t[0],t[1]]; 
            arr[i][4]=s_path[3]; 
            openlist[openlist.length]=arr[i];//将F等信息保存到openlist 
        } 
        if(maptt.rows[t[1]].cells[t[0]].style.backgroundColor!="#cccccc"&&maptt.rows[t[1]].cells[t[0]].style.backgroundColor!="#0000ff"&&maptt.rows[t[1]].cells[t[0]].style.backgroundColor!="#ff0000"&&maptt.rows[t[1]].cells[t[0]].style.backgroundColor!="#00ff00") 
        { 
            maptt.rows[t[1]].cells[t[0]].style.backgroundColor="#FF00FF"; 
            if(F!=undefined) 
            maptt.rows[t[1]].cells[t[0]].innerHTML="<font color=&#39;black&#39;>"+F+"</font>"; 
        } 
    } 
} 
function IsStart(arr){ //判断该点是不是起点 
    if(arr[0]==p_start[0]&&arr[1]==p_start[1]) 
        return true; 
    return false; 
} 
function IsInTurn(arr){ //判断是否是拐角 
    if(arr[0]>s_path[3][0]){ 
        if(arr[1]>s_path[3][1]){ 
            if(IsPass((arr[0]-1)+","+arr[1])||IsPass(arr[0]+","+(arr[1]-1))) 
                return false; 
        } 
        else if(arr[1]<s_path[3][1]){ 
            if(IsPass((arr[0]-1)+","+arr[1])||IsPass(arr[0]+","+(arr[1]+1))) 
                return false; 
        } 
    } 
    else if(arr[0]<s_path[3][0]){ 
        if(arr[1]>s_path[3][1]){ 
            if(IsPass((arr[0]+1)+","+arr[1])||IsPass(arr[0]+","+(arr[1]-1))) 
                return false; 
        } 
        else if(arr[1]<s_path[3][1]){ 
            if(IsPass((arr[0]+1)+","+arr[1])||IsPass(arr[0]+","+(arr[1]+1))) 
                return false; 
        } 
    } 
    return true; 
} 
function IsOutScreen(arr){ //是否超出场景范围 
    if(arr[0]<0||arr[1]<0||arr[0]>(w-1)||arr[1]>(h-1)) 
        return true; 
    return false; 
} 
function InOpen(arr){//获得传入在openlist数组的位置，如不存在返回false，存在为true，位置索引保存全局变量num中。 
    var bool=false; 
    for(var i=0;i<openlist.length;i++){ 
        if(arr[0]==openlist[i][3][0]&&arr[1]==openlist[i][3][1]){ 
            bool=true;num=i;break;} 
    } 
    return bool; 
} 
function InClose(arr){ 
    var bool=false; 
    for(var i=0;i<closelist.length;i++){ 
        if((arr[0]==closelist[i][3][0])&&(arr[1]==closelist[i][3][1])){ 
            bool=true;break;} 
    } 
    return bool; 
} 
function IsPass(pos){ //pos这个点是否和障碍点重合  
    if((";"+n_path+";").indexOf(";"+pos+";")!=-1) 
        return true; 
    return false; 
} 
function Sort(arr){//整理数组，找出最小的F，放在最后的位置。 
    var temp; 
    for(var i=0;i<arr.length;i++){ 
        if(arr.length==1)break; 
        if(arr[i][0]<=arr[i+1][0]){ 
            temp=arr[i]; 
            arr[i]=arr[i+1]; 
            arr[i+1]=temp; 
        } 
        if((i+1)==(arr.length-1)) 
            break; 
    } 
} 
function main(){//主函数 
        alert(&#39;&#39;); 
        GetF(//把原点周围8点传入GetF进行处理。算A*核心函数了 :)，进行求F，更新openlist数组 
            GetRound(s_path[3]) //求原点周围8点 
        ); 
    debugp.innerHTML+="A："+openlist.join(&#39;|&#39;)+"<br />";//调试 
        Sort(openlist);//整理数组，找出最小的F，放在最后的位置。 
    debugp.innerHTML+="B："+openlist.join(&#39;|&#39;)+"<br />";//调试 
        s_path=openlist[openlist.length-1];//设置当前原点为F最小的点 
        closelist[closelist.length]=s_path;//讲当前原点增加进closelist数组中 
        openlist[openlist.length-1]=null;//从openlist中清除F最小的点 
    debugp.innerHTML+="C："+openlist.join(&#39;|&#39;)+"<br />";//调试 
        if(openlist.length==0){alert("Can&#39;t Find the way");return;}//如果openlist数组中没有数据了，则找不到路径 
        openlist.length=openlist.length-1;//上次删除把数据删了，位置还保留了，这里删除 
        if((s_path[3][0]==p_end[0])&&(s_path[3][1]==p_end[1])){//如果到到终点了，描绘路径 
            getPath(); 
        } 
        else{//否则循环执行,标准原点 
            maptt.rows[s_path[3][1]].cells[s_path[3][0]].style.backgroundColor="green";setTimeout("main()",100); 
        } 
} 
function getPath(){//描绘路径 
    var str=""; 
    var t=closelist[closelist.length-1][4]; 
    while(1){ 
        str+=t.join(",")+";"; 
        maptt.rows[t[1]].cells[t[0]].style.backgroundColor="#ffff00"; 
        for(var i=0;i<closelist.length;i++){ 
            if(closelist[i][3][0]==t[0]&&closelist[i][3][1]==t[1]) 
                t=closelist[i][4]; 
        } 
        if(t[0]==p_start[0]&&t[1]==p_start[1]) 
            break; 
    } 
    alert(str); 
} 
function setPos(){//初始原点为起点 
    var h=(Math.abs(p_end[0]-p_start[0])+Math.abs(p_end[1]-p_start[1]))*gw; 
    s_path=[h,0,h,p_start,p_start]; 
} 
function set(id,arr){//设置点的类型 
    switch(id){ 
        case 1: 
            p_start=arr; 
            maptt.rows[arr[1]].cells[arr[0]].style.backgroundColor="#ff0000";break; 
        case 2: 
            p_end=arr;maptt.rows[arr[1]].cells[arr[0]].style.backgroundColor="#0000ff";break; 
        case 3: 
            n_path+=arr.join(",")+";";maptt.rows[arr[1]].cells[arr[0]].style.backgroundColor="#cccccc";break; 
        default: 
            break; 
    } 
} 
function setflag(id){flag=id;} 
</script> 
<table id="maptt" cellspacing="1" cellpadding="0" border="0" bgcolor="#000000"> 
<script> 
for(var i=0;i<h;i++){ 
    document.write("<tr>"); 
    for(var j=0;j<w;j++){ 
        document.write(&#39;<td onclick="set(flag,[&#39;+j+&#39;,&#39;+i+&#39;]);" bgcolor="#ffffff" width="20" height="20"></td>&#39;); 
    } 
    document.write("</tr>"); 
} 
</script> 
</table> 
<a href="javascript:setflag(1);">StarPoint</a><br> 
<a href=&#39;javascript:setflag(2);&#39;>EndPoint</a><br> 
<a href=&#39;javascript:setflag(3);&#39;>Wall</a><br> 
<input type="button" onclick="setPos();main();this.disabled=true;" value="find"> 
<p id="debugp"></p> 
</body> 
</html>