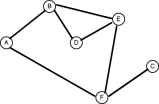
PHP 마스터 | PHP 개발자의 데이터 구조 : 그래프-PHP 튜토리얼-php.cn

집

백엔드 개발

PHP 튜토리얼

PHP 마스터 | PHP 개발자의 데이터 구조 : 그래프

Joseph Gordon-Levitt

Feb 23, 2025 am 08:49 AM

키 테이크 아웃

$그래프는 키/값 쌍 간의 관계를 모델링하는 데 사용되는 수학적 구성이며 네트워크 최적화, 트래픽 라우팅 및 소셜 네트워크 분석과 같은 수많은 실제 응용 프로그램이 있습니다. 그것들은 연결되거나 방향으로 지시되거나 무게가 가중되거나 비가운 상태로 연결되는 정점 (노드)과 가장자리 (선)로 구성되어 있습니다. 그래프는 두 가지 방식으로 표시 될 수 있습니다 : 인접 행렬 또는 인접력 목록으로. 인접성 목록은 특히 대부분의 정점 쌍이 연결되지 않은 희소 그래프의 경우 더 공간 효율적이며 인접한 행렬은 더 빠른 조회를 용이하게합니다.$

. 그래프 이론의 일반적인 적용은 두 노드 사이에서 최소한의 홉 (즉, 가장 짧은 경로)을 찾는 것입니다. 이는 지정된 루트 노드에서 그래프 레벨을 레벨별로 트래버하는 것을 포함하는 폭이 큰 검색을 사용하여 달성 할 수 있습니다. 이 프로세스는 방문하지 않은 노드의 대기열을 유지해야합니다 Dijkstra의 알고리즘은 그래프의 두 노드 사이에서 가장 짧거나 가장 최적의 경로를 찾는 데 널리 사용됩니다. 여기에는 소스 노드에서 시작하여 가능한 모든 정점 쌍 사이의 각 모서리를 검사하고 대상 노드에 도달 할 때까지 총 거리가 가장 짧은 업데이트 된 정점 세트를 유지하는 것이 포함됩니다. 이전 기사 중 하나에서 트리 데이터 구조를 소개했습니다. 이제 관련 구조 인 그래프를 탐색하고 싶습니다. 그래프에는 네트워크 최적화, 트래픽 라우팅 및 소셜 네트워크 분석과 같은 여러 실제 응용 프로그램이 있습니다. Google의 PageRank, Facebook의 그래프 검색 및 Amazon 및 Netflix의 권장 사항은 그래프 구동 응용 프로그램의 예입니다. 이 기사에서는 그래프가 사용되는 두 가지 일반적인 문제, 즉 홉 수와 가장 짧은 경로 문제를 살펴 보겠습니다. 그래프는 키/값 쌍 간의 관계를 모델링하는 데 사용되는 수학적 구조입니다. 그래프는 (노드) 세트와 연결하는 가장자리 (라인) 세트로 구성됩니다. 이 가장자리는 지시되거나 변신되지 않을 수 있습니다. 방향 가장자리는 단순히 두 정점 사이의 가장자리이며 가장자리 A → B는 B → A와 동일하지 않습니다. 방향이없는 가장자리에는 방향이나 방향이 없습니다. 에지 A-B는 B-A와 같습니다. 우리가 지난번에 대해 배운 나무 구조는 각 정점이 간단한 경로에 의해 적어도 하나의 다른 정점에 연결된 유형의 거부되지 않은 그래프로 간주 될 수 있습니다. 그래프는 가중치가 높거나 비가 중지 될 수도 있습니다. 가중 그래프 또는 네트워크는 가중치 또는 비용 값이 각 모서리에 할당되는 것입니다. 가중 그래프는 일반적으로 가장 최적의 경로, 가장 편리한 또는 가장 낮은 "비용"경로를 결정하는 데 일반적으로 사용됩니다. Googlemap의 주행 방향은 가중 그래프를 사용하는 예입니다. 최소 수의 홉 수 그래프 이론의 일반적인 적용은 두 노드 사이에서 가장 적은 수의 홉을 찾는 것입니다. 나무와 마찬가지로, 그래프는 깊이 우선 또는 폭 최초의 두 가지 방법 중 하나로 가로 질 수 있습니다. 이전 기사에서 깊이 우선 검색을 다루었으므로 폭이 먼저 검색을 살펴 보겠습니다. 다음 그래프를 고려하십시오. 단순성을 위해 그래프가 > 변형 된

라고 가정 해 봅시다. 즉, 모든 방향의 가장자리가 동일합니다. 우리의 임무는 두 노드 사이에서 가장 적은 수의 홉을 찾는 것입니다. 폭이 넓은 검색에서, 우리는 루트 노드 (또는 루트로 지정된 노드)에서 시작하여 레벨을 레벨로 내려 가면서 작동합니다. 이를 위해서는 방문하지 않은 노드 목록을 유지하려면 각 레벨 후에 역 추적하고 처리 할 수 있도록 대기열이 필요합니다. 일반 알고리즘은 다음과 같습니다.

그러나 먼저 그래프를 가로지 않고 방문하지 않고 어떤 노드가 인접 해 있는지 어떻게 알 수 있습니까? 이로 인해 그래프 데이터 구조를 모델링 할 수있는 문제가 발생합니다. 그래프를 나타내는 두 가지 방법은 일반적으로 인접성 행렬 또는 인접력 목록입니다. 인접성 목록으로 표시되는 위의 그래프는 다음과 같습니다.

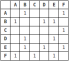PHP 마스터 | PHP 개발자의 데이터 구조 : 그래프 매트릭스로 표시되는 그래프는 다음과 같습니다. 여기서 1은 2 개의 정점 사이의 모서리의 "발생"을 나타냅니다.

PHP 마스터 | PHP 개발자의 데이터 구조 : 그래프 인접력 목록은 특히 대부분의 정점 쌍이 연결되지 않은 희소 그래프의 경우 공간 효율적이며 인접한 행렬은 더 빠른 조회를 용이하게합니다. 궁극적으로 표현 선택은 어떤 유형의 그래프 작업이 필요한지에 따라 다릅니다. 인접성 목록을 사용하여 그래프를 나타냅니다.

그리고 이제 일반적인 폭 넓은 첫 번째 검색 알고리즘의 구현이 무엇인지 살펴 보겠습니다.

1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

다음 예제를 실행하면 다음과 같습니다.

<span><span><?php </span></span><span><span>$graph = array(
</span></span><span>  <span>'A' => array('B', 'F'),
</span></span><span>  <span>'B' => array('A', 'D', 'E'),
</span></span><span>  <span>'C' => array('F'),
</span></span><span>  <span>'D' => array('B', 'E'),
</span></span><span>  <span>'E' => array('B', 'D', 'F'),
</span></span><span>  <span>'F' => array('A', 'E', 'C'),
</span></span><span><span>);</span></span></span>

우리가 큐 대신 스택을 사용했다면, 트래버스는 깊이 우선 검색이됩니다. 가장 짧은 경로 찾기

<span><span><?php </span></span><span><span>class Graph
</span></span><span><span>{
</span></span><span>  <span>protected $graph;
</span></span><span>  <span>protected $visited = array();
</span></span><span>
</span><span>  <span>public function __construct($graph) {
</span></span><span>    <span>$this->graph = $graph;
</span></span><span>  <span>}
</span></span><span>
</span><span>  <span>// find least number of hops (edges) between 2 nodes
</span></span><span>  <span>// (vertices)
</span></span><span>  <span>public function breadthFirstSearch($origin, $destination) {
</span></span><span>    <span>// mark all nodes as unvisited
</span></span><span>    <span>foreach ($this->graph as $vertex => $adj) {
</span></span><span>      <span>$this->visited[$vertex] = false;
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>// create an empty queue
</span></span><span>    <span>$q = new SplQueue();
</span></span><span>
</span><span>    <span>// enqueue the origin vertex and mark as visited
</span></span><span>    <span>$q->enqueue($origin);
</span></span><span>    <span>$this->visited[$origin] = true;
</span></span><span>
</span><span>    <span>// this is used to track the path back from each node
</span></span><span>    <span>$path = array();
</span></span><span>    <span>$path[$origin] = new SplDoublyLinkedList();
</span></span><span>    <span>$path[$origin]->setIteratorMode(
</span></span><span>      <span>SplDoublyLinkedList<span>::</span>IT_MODE_FIFO|SplDoublyLinkedList<span>::</span>IT_MODE_KEEP
</span></span><span>    <span>);
</span></span><span>
</span><span>    <span>$path[$origin]->push($origin);
</span></span><span>
</span><span>    <span>$found = false;
</span></span><span>    <span>// while queue is not empty and destination not found
</span></span><span>    <span>while (!$q->isEmpty() && $q->bottom() != $destination) {
</span></span><span>      <span>$t = $q->dequeue();
</span></span><span>
</span><span>      <span>if (!empty($this->graph[$t])) {
</span></span><span>        <span>// for each adjacent neighbor
</span></span><span>        <span>foreach ($this->graph[$t] as $vertex) {
</span></span><span>          <span>if (!$this->visited[$vertex]) {
</span></span><span>            <span>// if not yet visited, enqueue vertex and mark
</span></span><span>            <span>// as visited
</span></span><span>            <span>$q->enqueue($vertex);
</span></span><span>            <span>$this->visited[$vertex] = true;
</span></span><span>            <span>// add vertex to current path
</span></span><span>            <span>$path[$vertex] = clone $path[$t];
</span></span><span>            <span>$path[$vertex]->push($vertex);
</span></span><span>          <span>}
</span></span><span>        <span>}
</span></span><span>      <span>}
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>if (isset($path[$destination])) {
</span></span><span>      <span>echo "<span><span>$origin</span> to <span>$destination</span> in "</span>, 
</span></span><span>        <span>count($path[$destination]) - 1,
</span></span><span>        <span>" hopsn";
</span></span><span>      <span>$sep = '';
</span></span><span>      <span>foreach ($path[$destination] as $vertex) {
</span></span><span>        <span>echo $sep, $vertex;
</span></span><span>        <span>$sep = '->';
</span></span><span>      <span>}
</span></span><span>      <span>echo "n";
</span></span><span>    <span>}
</span></span><span>    <span>else {
</span></span><span>      <span>echo "No route from <span><span>$origin</span> to <span>$destinationn</span>"</span>;
</span></span><span>    <span>}
</span></span><span>  <span>}
</span></span><span><span>}</span></span></span>

또 다른 일반적인 문제는 두 노드 사이에서 가장 최적의 경로를 찾는 것입니다. 앞서 나는 Googlemap의 운전 방향을 이것의 예로 언급했다. 다른 응용 프로그램에는 여행 일정 계획, 도로 교통 관리 및 기차/버스 일정이 포함됩니다. 이 문제를 해결하기위한 가장 유명한 알고리즘 중 하나는 1959 년에 Edsger W. Dijkstra라는 이름으로 29 세의 컴퓨터 과학자가 발명했습니다. 일반적으로 Dijkstra의 솔루션은 소스 노드에서 시작하여 가능한 모든 정점 쌍 사이의 각 모서리를 검사하고 대상 노드에 도달하거나 도달 할 때까지 총 거리가 가장 짧은 업데이트 된 정점 세트를 유지하는 것이 포함됩니다. 솔루션을 구현하는 방법에는 여러 가지가 있으며 실제로 1959 년 이후 수년에 걸쳐 Minheaps, Priorityqueues 및 Fibonacci 힙을 사용하여 많은 개선 사항이 Dijkstra의 원래 알고리즘으로 만들어졌습니다. 일부 성능은 개선 된 반면, 다른 성능은 Dijkstra의 솔루션의 단점을 해결하도록 설계되었습니다. 가중치가 가중 그래프 만 작동했기 때문입니다 (가중치가 양수 값 인 경우). 다음은 (긍정적 인) 가중치 그래프의 예입니다.

다음과 같이이 그래프를 인접성 목록으로 표시 할 수 있습니다.

1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

다음은 PriorityQueue를 사용하여 모든 "최적화되지 않은"정점의 목록을 유지하는 구현입니다.

<span><span><?php </span></span><span><span>$graph = array(
</span></span><span>  <span>'A' => array('B', 'F'),
</span></span><span>  <span>'B' => array('A', 'D', 'E'),
</span></span><span>  <span>'C' => array('F'),
</span></span><span>  <span>'D' => array('B', 'E'),
</span></span><span>  <span>'E' => array('B', 'D', 'F'),
</span></span><span>  <span>'F' => array('A', 'E', 'C'),
</span></span><span><span>);</span></span></span>

보시다시피, Dijkstra의 솔루션은 단순히 폭이 큰 검색의 변형입니다! 다음 예제를 실행하면 다음 결과가 나옵니다.

<span><span><?php </span></span><span><span>class Graph
</span></span><span><span>{
</span></span><span>  <span>protected $graph;
</span></span><span>  <span>protected $visited = array();
</span></span><span>
</span><span>  <span>public function __construct($graph) {
</span></span><span>    <span>$this->graph = $graph;
</span></span><span>  <span>}
</span></span><span>
</span><span>  <span>// find least number of hops (edges) between 2 nodes
</span></span><span>  <span>// (vertices)
</span></span><span>  <span>public function breadthFirstSearch($origin, $destination) {
</span></span><span>    <span>// mark all nodes as unvisited
</span></span><span>    <span>foreach ($this->graph as $vertex => $adj) {
</span></span><span>      <span>$this->visited[$vertex] = false;
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>// create an empty queue
</span></span><span>    <span>$q = new SplQueue();
</span></span><span>
</span><span>    <span>// enqueue the origin vertex and mark as visited
</span></span><span>    <span>$q->enqueue($origin);
</span></span><span>    <span>$this->visited[$origin] = true;
</span></span><span>
</span><span>    <span>// this is used to track the path back from each node
</span></span><span>    <span>$path = array();
</span></span><span>    <span>$path[$origin] = new SplDoublyLinkedList();
</span></span><span>    <span>$path[$origin]->setIteratorMode(
</span></span><span>      <span>SplDoublyLinkedList<span>::</span>IT_MODE_FIFO|SplDoublyLinkedList<span>::</span>IT_MODE_KEEP
</span></span><span>    <span>);
</span></span><span>
</span><span>    <span>$path[$origin]->push($origin);
</span></span><span>
</span><span>    <span>$found = false;
</span></span><span>    <span>// while queue is not empty and destination not found
</span></span><span>    <span>while (!$q->isEmpty() && $q->bottom() != $destination) {
</span></span><span>      <span>$t = $q->dequeue();
</span></span><span>
</span><span>      <span>if (!empty($this->graph[$t])) {
</span></span><span>        <span>// for each adjacent neighbor
</span></span><span>        <span>foreach ($this->graph[$t] as $vertex) {
</span></span><span>          <span>if (!$this->visited[$vertex]) {
</span></span><span>            <span>// if not yet visited, enqueue vertex and mark
</span></span><span>            <span>// as visited
</span></span><span>            <span>$q->enqueue($vertex);
</span></span><span>            <span>$this->visited[$vertex] = true;
</span></span><span>            <span>// add vertex to current path
</span></span><span>            <span>$path[$vertex] = clone $path[$t];
</span></span><span>            <span>$path[$vertex]->push($vertex);
</span></span><span>          <span>}
</span></span><span>        <span>}
</span></span><span>      <span>}
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>if (isset($path[$destination])) {
</span></span><span>      <span>echo "<span><span>$origin</span> to <span>$destination</span> in "</span>, 
</span></span><span>        <span>count($path[$destination]) - 1,
</span></span><span>        <span>" hopsn";
</span></span><span>      <span>$sep = '';
</span></span><span>      <span>foreach ($path[$destination] as $vertex) {
</span></span><span>        <span>echo $sep, $vertex;
</span></span><span>        <span>$sep = '->';
</span></span><span>      <span>}
</span></span><span>      <span>echo "n";
</span></span><span>    <span>}
</span></span><span>    <span>else {
</span></span><span>      <span>echo "No route from <span><span>$origin</span> to <span>$destinationn</span>"</span>;
</span></span><span>    <span>}
</span></span><span>  <span>}
</span></span><span><span>}</span></span></span>

요약 이 기사에서 나는 그래프 이론의 기본, 그래프를 나타내는 두 가지 방법 및 그래프 이론의 적용에있어 두 가지 근본적인 문제를 소개했습니다. 두 노드 사이에서 가장 적은 수의 홉을 찾는 데 너비가 최초의 검색이 사용되는 방법과 Dijkstra의 솔루션이 두 노드 사이에서 가장 짧은 경로를 찾는 데 어떻게 사용되는지 보여주었습니다. Fotolia를 통한 이미지 데이터 구조의 그래프에 대한 자주 묻는 질문 (FAQ) 데이터 구조에서 그래프와 트리의 차이점은 무엇입니까?

그래프와 트리는 모두 비선형 데이터 구조이지만 몇 가지 주요 차이점이 있습니다. 트리는 그래프 유형이지만 모든 그래프가 나무가 아닙니다. 트리는 사이클이없는 연결된 그래프입니다. 루트 노드 및 하위 노드가있는 계층 구조가 있습니다. 트리의 각 노드는 루트에서 고유 한 경로를 가지고 있습니다. 반면에 그래프는 사이클을 가질 수 있고 그 구조는 더 복잡합니다. 연결 또는 연결이 끊어지고 노드 사이에 여러 경로가있을 수 있습니다. 데이터 구조에 그래프가 어떻게 표시됩니까?

데이터 구조의 그래프는 두 가지 방식으로 표시 될 수 있습니다 : 인접 매트릭스와 인접성 목록. 인접 매트릭스는 크기 V X V의 2D 배열입니다. 여기서 v는 그래프의 정점 수입니다. 정점 I와 J 사이에 가장자리가있는 경우, 행 I과 열 j의 교차점의 셀은 1이됩니다. 그렇지 않으면 0이됩니다. 인접성 목록은 링크 된 목록의 배열입니다. 배열의 인덱스는 정점을 나타내고 연결된 목록의 각 요소는 정점과 가장자리를 형성하는 다른 정점을 나타냅니다.

데이터 구조의 그래프 유형은 무엇입니까? 데이터 구조의 여러 유형의 그래프입니다. 간단한 그래프는 루프가없고 두 개의 정점 사이에 하나 이상의 가장자리가없는 그래프입니다. 멀티 그래프는 정점 사이에 여러 개의 가장자리를 가질 수 있습니다. 완전한 그래프는 모든 정점 쌍이 가장자리로 연결되는 간단한 그래프입니다. 가중 그래프는 각 모서리에 가중치를 할당합니다. 지시 된 그래프 (또는 digraph)에는 방향이있는 가장자리가 있습니다. 가장자리는 한 정점에서 다른 정점으로 가리 킵니다 컴퓨터 과학에서 그래프의 응용은 무엇입니까?

그래프는 컴퓨터 과학의 수많은 응용 분야에서 사용됩니다. 그들은 소셜 네트워크에서 사람들 사이의 연결을 나타내는 데 사용됩니다. 웹 크롤링에 사용되어 웹 페이지를 방문하고 검색 색인을 구축합니다. 네트워크 라우팅 알고리즘에 사용되어 두 노드 사이의 최상의 경로를 찾습니다. 생물학에서 생물학적 네트워크를 모델링하고 분석하는 데 사용됩니다. 컴퓨터 그래픽 및 물리 시뮬레이션에도 사용됩니다.

그래프 트래버스 알고리즘은 무엇입니까?

두 가지 주요 그래프 트래버스 알고리즘 : 깊이 우선 검색 (DFS)과 폭이 큰 검색이 있습니다. (BFS). DFS는 역 추적 전에 각 지점을 따라 가능한 한 멀리 탐색합니다. 스택 데이터 구조를 사용합니다. BFS는 다음 단계로 가기 전에 현재 깊이의 모든 정점을 탐색합니다. 큐 데이터 구조를 사용합니다.

java에서 그래프를 구현하는 방법?

Java에서는 해시 맵을 사용하여 인접 목록을 저장하는 그래프를 구현할 수 있습니다. 해시 맵의 각 키는 정점이며 그 값은 연결된 정점을 포함하는 링크 사전 목록입니다.

양파 그래프 란 무엇입니까?

이당 그래프는 정점이 할 수있는 그래프입니다. 모든 에지가 한 세트의 정점을 다른 세트의 정점에 연결하도록 두 개의 분리 된 세트로 나뉩니다. Edge는 동일한 세트 내에서 정점을 연결합니다.

하위 그래프 란 무엇입니까?

하위 그래프는 다른 그래프의 일부인 그래프입니다. 그것은 원본 그래프의 일부 (또는 전부) 원래 그래프의 일부 (또는 일부) 가장자리를 가지고 있습니다.

그래프의 사이클은 무엇입니까?

그래프의 사이클은 다음과 같습니다. 동일한 정점에서 시작하고 끝나고 끝이 하나 이상인 경로. 그래프의 경로는 무엇입니까? 그래프의 경로는 각 쌍이 각 쌍의 정점 시퀀스입니다. ~의 연속 정점은 가장자리로 연결됩니다

위 내용은 PHP 마스터 | PHP 개발자의 데이터 구조 : 그래프의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

성명

본 글의 내용은 네티즌들의 자발적인 기여로 작성되었으며, 저작권은 원저작자에게 있습니다. 본 사이트는 이에 상응하는 법적 책임을 지지 않습니다. 표절이나 침해가 의심되는 콘텐츠를 발견한 경우 admin@php.cn으로 문의하세요.

핫 AI 도구

Undresser.AI Undress

사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover

사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool

무료로 이미지를 벗다

Clothoff.io

AI 옷 제거제

AI Hentai Generator

AI Hentai를 무료로 생성하십시오.

뜨거운 도구

ZendStudio 13.5.1 맥

강력한 PHP 통합 개발 환경

WebStorm Mac 버전

유용한 JavaScript 개발 도구

메모장++7.3.1

사용하기 쉬운 무료 코드 편집기

mPDF

mPDF는 UTF-8로 인코딩된 HTML에서 PDF 파일을 생성할 수 있는 PHP 라이브러리입니다. 원저자인 Ian Back은 자신의 웹 사이트에서 "즉시" PDF 파일을 출력하고 다양한 언어를 처리하기 위해 mPDF를 작성했습니다. HTML2FPDF와 같은 원본 스크립트보다 유니코드 글꼴을 사용할 때 속도가 느리고 더 큰 파일을 생성하지만 CSS 스타일 등을 지원하고 많은 개선 사항이 있습니다. RTL(아랍어, 히브리어), CJK(중국어, 일본어, 한국어)를 포함한 거의 모든 언어를 지원합니다. 중첩된 블록 수준 요소(예: P, DIV)를 지원합니다.

MinGW - Windows용 미니멀리스트 GNU

이 프로젝트는 osdn.net/projects/mingw로 마이그레이션되는 중입니다. 계속해서 그곳에서 우리를 팔로우할 수 있습니다. MinGW: GCC(GNU Compiler Collection)의 기본 Windows 포트로, 기본 Windows 애플리케이션을 구축하기 위한 무료 배포 가능 가져오기 라이브러리 및 헤더 파일로 C99 기능을 지원하는 MSVC 런타임에 대한 확장이 포함되어 있습니다. 모든 MinGW 소프트웨어는 64비트 Windows 플랫폼에서 실행될 수 있습니다.