집 >백엔드 개발 >PHP 튜토리얼 >이진 트리의 역방향 홀수 레벨

이진 트리의 역방향 홀수 레벨

Linda Hamilton원래의: 2025-01-01 04:15:10360검색

2415. 이진 트리의 역방향 홀수 레벨

난이도:중

주제: 트리, 깊이 우선 검색, 너비 우선 검색, 이진 트리

완벽한 이진 트리의 루트가 주어지면 트리의 각 홀수 수준에서 노드 값을 반대로 바꿉니다.

예를 들어 레벨 3의 노드 값이 [2,1,3,4,7,11,29,18]이라고 가정하면 [18,29,11,7,4,3,1]이 되어야 합니다. ,2].

역트리의 루트를 반환합니다.

모든 상위 노드에 두 개의 하위 노드가 있고 모든 리프가 동일한 수준에 있는 경우 이진 트리는 완벽합니다.

노드의 레벨은 해당 노드와 루트 노드 사이의 경로를 따라 있는 에지 수입니다.

예 1:

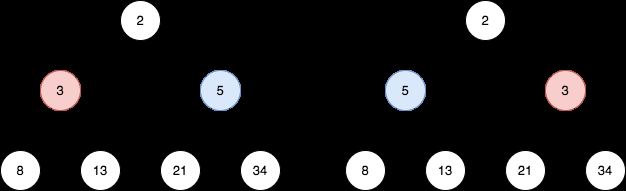
Reverse Odd Levels of Binary Tree

입력: 루트 = [2,3,5,8,13,21,34]
출력: [2,5,3,8,13,21,34]
설명:
- 나무에는 홀수 레벨이 하나만 있습니다.
- 레벨 1의 노드는 각각 3, 5인데, 이를 뒤집어서 5, 3이 됩니다.

예 2:

Reverse Odd Levels of Binary Tree

입력: 루트 = [7,13,11]
출력: [7,11,13]
설명:
- 레벨 1의 노드는 13, 11인데, 이를 뒤집어서 11, 13이 됩니다.

예 3:

입력: 루트 = [0,1,2,0,0,0,0,1,1,1,1,2,2,2,2]
출력: [0,2,1,0,0,0,0,2,2,2,2,1,1,1,1]
설명:
- 홀수 레벨에는 0이 아닌 값이 있습니다.
- 레벨 1의 노드는 1, 2였고 반전 이후에는 2, 1이 되었습니다.
- 레벨 3의 노드는 1, 1, 1, 1, 2, 2, 2, 2였으며 반전 이후에는 2, 2, 2, 2, 1, 1, 1, 1이 됩니다.

제약조건:

트리의 노드 수는 [1, 2¹⁴] 범위에 있습니다.
0 <= Node.val <= 10⁵
루트는 완전 이진 트리입니다.

힌트:

각 레벨을 독립적으로 재귀적으로 풀어보세요.
깊이 우선 검색을 수행하는 동안 왼쪽 및 오른쪽 노드(페어링되어야 함)를 다음 레벨로 전달합니다. 현재 레벨이 홀수이면 해당 값을 반전하거나, 그렇지 않으면 재귀적으로 다음 레벨로 이동합니다.

해결책:

이진 트리에서 깊이 우선 순회를 수행해야 합니다. 작업은 홀수 수준에서 노드 값을 바꾸는 것입니다. 완벽한 이진 트리는 리프가 아닌 모든 노드에 두 개의 자식이 있고 모든 리프 노드가 동일한 수준에 있음을 의미합니다.

DFS(깊이 우선 검색) 접근 방식을 사용하고 홀수 레벨마다 노드 값을 반전시킵니다. 다음은 이를 수행하는 솔루션입니다.

핵심 포인트:

나무는 완벽합니다. 즉, 완전히 균형이 잡혀 있고 모든 잎 노드가 동일한 수준에 있다는 의미입니다.
홀수 레벨의 노드만 되돌려야 합니다. 홀수 레벨은 레벨 1(1, 3, 5 등)부터 색인이 생성됩니다.
DFS를 사용하여 트리를 탐색하고 노드 수준을 식별할 수 있습니다. 이상한 레벨을 만나면 해당 레벨의 노드 값을 교환합니다.
각 수준에서 두 개의 하위 노드, 즉 왼쪽 하위 노드와 오른쪽 하위 노드를 순회합니다.

접근하다:

트리의 깊이 우선 순회를 수행합니다.
현재 수준의 각 노드 쌍에 대해:
- 레벨이 홀수이면 노드 값을 교환하세요.
현재 노드의 왼쪽 및 오른쪽 하위 항목을 재귀적으로 처리하여 업데이트된 레벨 정보를 전달합니다.
전체 트리를 처리한 후 루트 노드를 반환합니다.

계획:

루트 노드에서 시작합니다.
재귀 함수 dfs를 사용하여 트리를 순회하고 홀수 수준의 노드 값을 역전시킵니다.
현재 레벨을 추적하여 이상한 레벨을 식별하세요.
홀수 수준의 값을 교환하고 하위 항목에 대해 DFS 순회를 계속합니다.
처리 후 루트를 반납합니다.

해결 단계:

재귀 함수 dfs($left, $right, $isOddLevel) 정의:
- 왼쪽: 왼쪽 하위 노드.
- 오른쪽: 오른쪽 하위 노드.
- isOddLevel: 현재 레벨이 홀수인지 여부를 나타내는 부울입니다.
왼쪽이 null인지 확인하세요. 그렇다면 더 이상 처리할 노드가 없으므로 반환하세요.
isOddLevel이 true인 경우 왼쪽 노드와 오른쪽 노드의 값을 바꿉니다.
다음에 대해 dfs 함수를 재귀적으로 호출합니다.
- 왼쪽의 왼쪽 자식과 오른쪽의 오른쪽 자식(다음 단계).
- 왼쪽의 오른쪽 자식과 오른쪽의 왼쪽 자식(다음 레벨).
dfs($root->left, $root->right, true)로 재귀를 시작하고 루트를 반환합니다.

이 솔루션을 PHP로 구현해 보겠습니다: 2415. 이진 트리의 역방향 홀수 레벨

<?php
class TreeNode {
    public $val = 0;
    public $left = null;
    public $right = null;

    public function __construct($val = 0, $left = null, $right = null) {
        $this->val = $val;
        $this->left = $left;
        $this->right = $right;
    }
}

class Solution {
    /**
     * @param TreeNode $root
     * @return TreeNode
     */
    public function reverseOddLevels($root) {
       ...
       ...
       ...
       /**
        * go to ./solution.php
        */
    }

    /**
     * Helper function to perform DFS
     *
     * @param $left
     * @param $right
     * @param $isOddLevel
     * @return void
     */
    private function dfs($left, $right, $isOddLevel) {
       ...
       ...
       ...
       /**
        * go to ./solution.php
        */
    }
}

// Example usage:
$root = new TreeNode(2);
$root->left = new TreeNode(3);
$root->right = new TreeNode(5);
$root->left->left = new TreeNode(8);
$root->left->right = new TreeNode(13);
$root->right->left = new TreeNode(21);
$root->right->right = new TreeNode(34);

$solution = new Solution();
$reversedRoot = $solution->reverseOddLevels($root);

// Function to print the tree for testing
function printTree($root) {
    if ($root === null) {
        return;
    }
    echo $root->val . " ";
    printTree($root->left);
    printTree($root->right);
}

printTree($reversedRoot); // Output: 2 5 3 8 13 21 34
?>

설명:

TreeNode 클래스: 값(val)과 두 개의 자식(왼쪽, 오른쪽)을 갖는 이진 트리 노드의 구조를 나타냅니다.
reverseOddLevels 함수: 루트 노드의 왼쪽 및 오른쪽 하위 항목으로 DFS를 시작하고 레벨 1(홀수 레벨)에서 시작합니다.
dfs 함수:
- 현재 레벨이 홀수인지 확인하기 위해 두 개의 노드(왼쪽 및 오른쪽)와 부울 isOddLevel을 사용합니다.
- 현재 레벨이 홀수이면 왼쪽과 오른쪽의 값이 바뀌게 됩니다.
- isOddLevel 값을 번갈아 가며 다음 레벨을 위해 자신을 재귀적으로 호출합니다(true는 false가 되고 그 반대도 마찬가지임).
재귀는 각 수준에서 다음 노드 쌍을 처리하여 홀수 수준의 노드만 반전되도록 합니다.

예제 연습:

예 1:

입력:

레벨 0: [2](균등, 변화 없음).
레벨 1: [3, 5] (홀수, [5, 3]의 반대).
레벨 2: [8, 13, 21, 34](균등, 변화 없음).

출력:

예 2:

입력:

       7
      / \
     13  11

레벨 0: [7](균등, 변화 없음).
레벨 1: [13, 11] (홀수, [11, 13]의 반대).

출력:

       7
      / \
     11  13

시간 복잡도:

시간 복잡도: O(n), 여기서 n은 이진 트리의 노드 수입니다. 깊이 우선 방식으로 각 노드를 정확히 한 번씩 방문합니다.
공간 복잡도: O(h), 여기서 h는 트리의 높이입니다. 재귀 깊이는 트리의 높이에 해당하며 최악의 경우(기울어진 트리의 경우) O(n)이 되지만 완전 이진 트리의 경우 O(log n)이 됩니다.

이 솔루션은 시간 복잡도가 O(n)인 깊이 우선 탐색을 사용하여 완전 이진 트리의 홀수 수준에 있는 노드를 효율적으로 역전시킵니다. 코드는 홀수 수준에서 값을 교환하고 재귀적 접근 방식을 사용하여 트리를 처리합니다.

연락처 링크

이 시리즈가 도움이 되었다면 GitHub에서 저장소에 별표를 표시하거나 즐겨찾는 소셜 네트워크에서 게시물을 공유해 보세요. 여러분의 지원은 저에게 큰 의미가 될 것입니다!

이런 유용한 콘텐츠를 더 원하시면 저를 팔로우해주세요.

링크드인
깃허브

위 내용은 이진 트리의 역방향 홀수 레벨의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

php Boolean NULL define if for while try continue using class number function this input github

성명：

이전 기사：내 파일 첨부가 PHPMailer로 전송되지 않는 이유는 무엇입니까?다음 기사：내 파일 첨부가 PHPMailer로 전송되지 않는 이유는 무엇입니까?