빅오 표기법 - 파이썬

1. 정의

알고리즘의 실행 시간이나 공간 사용량의 상한을 설명하는 수학적 표기법입니다. O(f(n))으로 표시하는데, 여기서 f(n)은 입력 n의 크기에 따른 시간이나 공간을 나타내는 함수이다. .

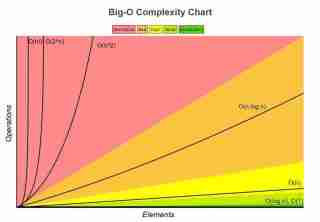
자세한 내용은 http://bigocheatsheet.com

을 참조하세요.

2. 목적

• 알고리즘 비교: 다양한 알고리즘을 비교하고 주어진 문제에 가장 효율적인 알고리즘을 선택할 수 있습니다.
• 확장성: 데이터 양이 증가할 때 알고리즘이 어떻게 작동할지 예측하는 데 도움이 됩니다.

3. 복잡성 분석

• 최악의 경우: 알고리즘이 더 오래 걸리거나 더 많은 리소스를 사용하는 시나리오를 말합니다. 빅오는 주로 이런 경우를 지칭합니다.
• 최고 사례 및 평균 사례: 중요하지만 Big O 표기법에서는 덜 자주 사용됩니다.

4. 우주 대 우주 시간

• 시간적 복잡도: 알고리즘이 실행되는 데 걸리는 시간을 말합니다.
• 공간 복잡도: 추가로 사용하는 메모리의 양을 나타냅니다. O(1)(상수 공간) 또는 O(n)(선형 공간)
과 같은 표기법을 사용할 수 있습니다.

예:

import timeit
import matplotlib.pyplot as plt
import cProfile

# O(1)


def constant_time_operation():
    return 42

# O(log n)


def logarithmic_time_operation(n):
    count = 0
    while n > 1:
        n //= 2
        count += 1
    return count

# O(n)


def linear_time_operation(n):
    total = 0
    for i in range(n):
        total += i
    return total

# O(n log n)


def linear_logarithmic_time_operation(n):
    if n 



<p><img src="/static/imghwm/default1.png" data-src="https://img.php.cn/upload/article/000/000/000/173189059010897.jpg?x-oss-process=image/resize,p_40" class="lazy" alt="Notación Big O - Python"></p>

<p>단순히 큰 표기법을 적용하는 것만으로는 충분하지 않으며 이것이 첫 번째 단계이기는 하지만 <strong>슬롯</strong>, 캐시, 스레드, 병렬 처리 등을 사용하여 메모리를 최적화하는 다른 방법이 있다는 점을 기억하세요. 프로세스 등</p>

<p>읽어주셔서 감사합니다!!<br>
반응하고 의견을 제시하여 지원해 주세요.</p>


          

            
        

위 내용은 빅오 표기법 - 파이썬의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!