np.einsum의 성능 조사
- Patricia Arquette원래의
- 2024-11-08 21:22:02777검색
내 마지막 블로그 게시물의 한 독자가 슬라이스 방식 matmul과 유사한 작업의 경우 매개변수 목록에서 최적화 플래그를 설정하지 않는 한 np.einsum이 np.matmul보다 상당히 느리다는 점을 지적했습니다. np.einsum(.. ., 최적화 = True).
다소 회의적인 마음으로 Jupyter 노트북을 실행하고 몇 가지 예비 테스트를 수행했습니다. 그리고 정말 망할 것입니다. 이는 완전히 사실입니다. 최적화가 전혀 차이를 가져서는 안되는 두 피연산자의 경우에도 마찬가지입니다!
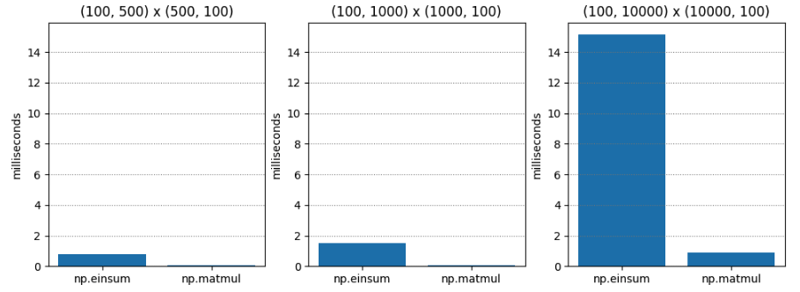
테스트 1은 매우 간단합니다. 다양한 차원의 두 C 순서(행 주요 순서라고도 함) 행렬의 행렬 곱셈입니다. np.matmul은 지속적으로 약 20배 더 빠릅니다.
| M1 | M2 | np.einsum | np.matmul | np.einsum / np.matmul |
|---|---|---|---|---|
| (100, 500) | (500, 100) | 0.765 | 0.045 | 17.055 |
| (100, 1000) | (1000, 100) | 1.495 | 0.073 | 20.554 |
| (100, 10000) | (10000, 100) | 15.148 | 0.896 | 16.899 |
테스트 2의 경우optim=True인 경우 결과가 크게 다릅니다. np.einsum은 여전히 느리지만 최악의 경우 약 1.5배만 느립니다!

| M1 | M2 | np.einsum | np.matmul | np.einsum / np.matmul |
|---|---|---|---|---|
| (100, 500) | (500, 100) | 0.063 | 0.043 | 1.474 |
| (100, 1000) | (1000, 100) | 0.086 | 0.067 | 1.284 |
| (100, 10000) | (10000, 100) | 1.000 | 0.936 | 1.068 |
왜?
최적화 플래그에 대해 제가 이해한 바는 피연산자가 3개 이상일 때 최적의 축소 순서를 결정한다는 것입니다. 여기에는 피연산자가 두 개뿐입니다. 그러니 최적화가 차이를 만들어서는 안 되겠죠?
하지만 최적화는 단순히 축소 순서를 선택하는 것 이상의 작업을 수행하는 것일까요? 아마도 최적화는 메모리 레이아웃을 인식하고 있으며 이는 행 주요 레이아웃과 열 주요 레이아웃과 관련이 있습니까?
초등학교의 행렬 곱셈 방법에서는 단일 항목을 계산하기 위해 op1의 행을 반복하고 op2의 열을 반복하므로 두 번째 인수를 열 우선 순서로 배치하면 속도가 향상될 수 있습니다. np.einsum의 경우(np.einsum이 초등학교에서 배운 행렬 곱셈 방법의 일반화된 버전과 비슷하다고 가정하면 이것이 사실일 것으로 의심됩니다).
그래서 테스트 3에서는 두 번째 피연산자에 대해 열 주요 행렬을 전달하여 최적화=False일 때 np.einsum의 속도가 빨라졌는지 확인했습니다.
결과는 다음과 같습니다. 놀랍게도 np.einsum은 여전히 상당히 더 나쁩니다. 분명히 내가 이해하지 못하는 일이 일어나고 있습니다. 아마도 최적화가 True일 때 np.einsum이 완전히 다른 코드 경로를 사용할까요? 발굴을 시작할 시간입니다.

| M1 | M2 | np.einsum | np.matmul | np.einsum / np.matmul |
|---|---|---|---|---|
| (100, 500) | (500, 100) | 1.486 | 0.056 | 26.541 |
| (100, 1000) | (1000, 100) | 3.885 | 0.125 | 31.070 |
| (100, 10000) | (10000, 100) | 49.669 | 1.047 | 47.444 |
더 깊게
Numpy 1.12.0의 릴리스 노트에는 최적화 플래그 도입이 언급되어 있습니다. 그러나 최적화의 목적은 피연산자 체인의 인수가 결합되는 순서(즉, 연관성)를 결정하는 것 같습니다. 따라서 최적화는 두 피연산자에 대해서만 차이를 만들어서는 안 됩니다. 그렇죠? 출시 노트는 다음과 같습니다.
np.einsum은 이제 수축 순서를 최적화하는 최적화 인수를 지원합니다. 예를 들어, np.einsum은 N^4처럼 확장되는 단일 패스에서 체인 도트 예제 np.einsum('ij,jk,kl->il', a, b, c)를 완성합니다. 그러나 Optimize=True일 때 np.einsum은 이 스케일링을 N^3 또는 효과적으로 np.dot(a, b).dot(c)로 줄이기 위해 중간 배열을 생성합니다. 스케일링을 줄이기 위해 중간 텐서를 사용하는 것이 일반적인 einsum 합계 표기법에 적용되었습니다. 자세한 내용은 np.einsum_path를 참조하세요.
이 미스터리를 더욱 복잡하게 만들기 위해 일부 이후 릴리스 노트에서는 np.einsum이 tensordot(해당되는 경우 자체적으로 BLAS를 사용함)를 사용하도록 업그레이드되었다고 나와 있습니다. 이제 그것은 유망해 보입니다.
그런데 최적화가 참일 때 속도 향상이 만 보이는 이유는 무엇입니까? 무슨 일이에요?
numpy/numpy/_core/einsumfunc.py에서 def einsum(*operands, out=None,optim=False, **kwargs)를 읽으면 거의 즉시 다음과 같은 조기 종료 논리에 도달하게 됩니다.
# If no optimization, run pure einsum
if optimize is False:
if specified_out:
kwargs['out'] = out
return c_einsum(*operands, **kwargs)
c_einsum은 텐소도트를 활용하나요? 나는 그것을 의심한다. 코드 후반부에서 1.14 노트가 참조하는 것으로 보이는 tensordot 호출을 볼 수 있습니다.
# Start contraction loop
for num, contraction in enumerate(contraction_list):
...
# Call tensordot if still possible
if blas:
...
# Contract!
new_view = tensordot(
*tmp_operands, axes=(tuple(left_pos), tuple(right_pos))
)
현재 상황은 다음과 같습니다:
- 최적화가 참이면 contraction_list 루프가 실행됩니다. 사소한 두 피연산자의 경우에도 마찬가지입니다.
- tensordot는 contraction_list 루프에서만 호출됩니다.
- 따라서 최적화가 True일 때 tensordot(따라서 BLAS)를 호출합니다.
제가 보기엔 이건 버그인 것 같습니다. IMHO, np.einsum 시작 부분의 "초기 종료"는 피연산자가 tensordot와 호환되는지 감지하고 가능하면 tensordot를 호출해야 합니다. 그러면 최적화가 False인 경우에도 확실한 BLAS 속도 향상을 얻을 수 있습니다. 결국 최적화의 의미는 BLAS의 사용이 아닌 축소 순서와 관련이 있으며 이는 당연하다고 생각합니다.
여기서 장점은 텐소도트 호출과 동일한 작업에 대해 np.einsum을 호출하는 사람이 적절한 속도 향상을 얻을 수 있어 성능 관점에서 np.einsum이 조금 덜 위험해진다는 것입니다.
c_einsum은 실제로 어떻게 작동하나요?
확인하기 위해 C 코드를 좀 살펴봤습니다. 구현의 핵심은 여기에 있습니다.
많은 인수 구문 분석 및 매개변수 준비 후에 축 반복 순서가 결정되고 특수 목적의 반복자가 준비됩니다. 반복자의 각 산출량은 모든 피연산자를 동시에 탐색하는 다양한 방법을 나타냅니다.
# If no optimization, run pure einsum
if optimize is False:
if specified_out:
kwargs['out'] = out
return c_einsum(*operands, **kwargs)
특정 특수 사례 최적화가 적용되지 않는다고 가정하면 관련된 데이터 유형을 기반으로 적절한 SOP(합계) 함수가 결정됩니다.
# Start contraction loop
for num, contraction in enumerate(contraction_list):
...
# Call tensordot if still possible
if blas:
...
# Contract!
new_view = tensordot(
*tmp_operands, axes=(tuple(left_pos), tuple(right_pos))
)
그런 다음 이 곱의 합계(sop) 연산은 다음과 같이 반복자에서 반환된 각 다중 피연산자 스트라이드에서 호출됩니다.
/* Allocate the iterator */
iter = NpyIter_AdvancedNew(nop+1, op, iter_flags, order, casting, op_flags,
op_dtypes, ndim_iter, op_axes, NULL, 0);
Einsum의 작동 방식은 이것이 제가 이해한 바입니다. 아직은 다소 미흡한 것은 사실입니다. 실제로는 제가 투자한 시간보다 더 많은 가치가 있습니다.
그러나 이는 초등학교에서 사용하는 행렬 곱셈 방법의 일반화된 기가브레인 버전처럼 작동한다는 내 의심을 확증해 줍니다. 궁극적으로 피연산자 사이를 이동하는 "스트라이더"에 의존하는 일련의 "곱의 합" 연산에 위임합니다. 이는 행렬 곱셈을 배울 때 손가락으로 수행하는 작업과 크게 다르지 않습니다.
요약
그렇다면 np.einsum을 최적화=True로 호출하면 일반적으로 더 빠른 이유는 무엇일까요? 이유는 두 가지입니다.
첫 번째(원래) 이유는 최적의 수축 경로를 찾으려고 하기 때문입니다. 그러나 앞서 지적했듯이 성능 테스트에서처럼 피연산자가 두 개뿐인 경우에는 문제가 되지 않습니다.
두 번째(및 더 새로운) 이유는optim=True인 경우 두 피연산자의 경우에도 가능한 경우 tensordot를 호출하는 코드 경로를 활성화하고 차례로 BLAS를 사용하려고 시도한다는 것입니다. 그리고 BLAS는 행렬 곱셈만큼 최적화되어 있습니다!
이제 두 피연산자 속도 향상 미스터리가 해결되었습니다! 그러나 우리는 수축 순서로 인한 속도 향상의 특성을 실제로 다루지 않았습니다. 그것은 미래의 게시물을 기다려야 할 것입니다! 계속 지켜봐주세요!
위 내용은 np.einsum의 성능 조사의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

