병합 정렬 알고리즘 이해: 정렬 알고리즘 마스터를 위한 초보자 가이드

이전 기사에서는 버블 정렬, 선택 정렬, 삽입 정렬 등 다양한 정렬 알고리즘에 대해 배웠습니다. 우리는 이러한 정렬 알고리즘이 구현하기가 매우 쉽지만 대규모 데이터 세트에는 효율적이지 않다는 것을 배웠습니다. 즉, 대규모 데이터 세트 정렬을 처리하려면 더 효율적인 알고리즘이 필요하므로 병합 정렬이 필요합니다. 이번 시리즈에서는 병합 정렬의 작동 방식과 이를 JavaScript로 구현하는 방법을 살펴보겠습니다. 준비됐나요?

목차

1. 병합 정렬 알고리즘이란 무엇인가요?
2. 병합 정렬 알고리즘의 작동 방식
   • 시간복잡도
   • 공간 복잡도
3. JavaScript로 구현
4. 결론

병합 정렬 알고리즘이란 무엇입니까?

병합 정렬 알고리즘은 분할 정복 원칙을 따르는 뛰어난 정렬 알고리즘입니다. 인접한 요소를 비교하여 배열을 여러 번 통과하는 선택 정렬 및 버블 정렬과 같은 간단한 알고리즘과 달리 병합 정렬은 보다 전략적인 접근 방식을 취합니다.

1. 분할: 먼저 병합 정렬로 배열을 두 부분으로 나눕니다
2. 정복: 둘째, 각 절반을 재귀적으로 정렬
3. 결합: 마지막으로 정렬된 절반을 다시 병합합니다

이 접근 방식은 대규모 데이터세트를 처리할 때 선택 정렬 및 버블 정렬과 같은 단순한 O(n²) 알고리즘보다 지속적으로 성능이 뛰어납니다.

병합 정렬 알고리즘의 작동 방식

우리는 널리 사용되는 분할 정복 접근 방식을 사용하여 병합 정렬이 작동하는 것을 확인했습니다. 아래는 작동 방식을 시각적으로 나타낸 것입니다.

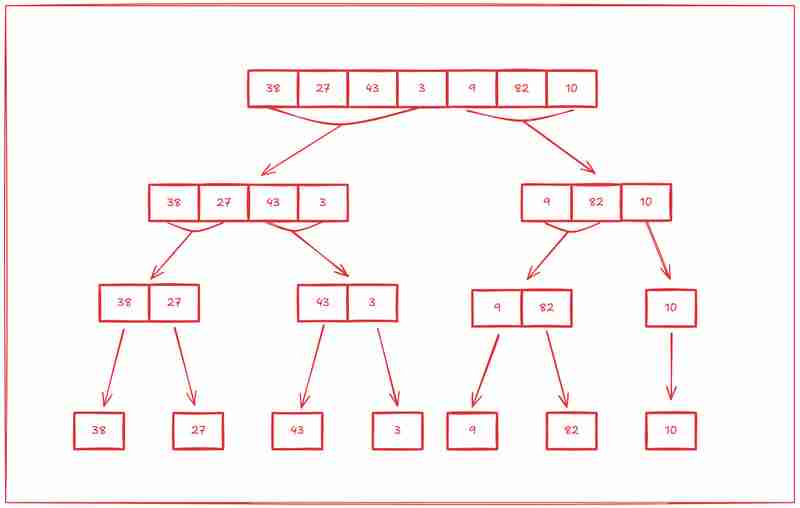
이제 마법을 보았으므로 위에서 언급한 접근 방식을 사용하여 [38, 27, 43, 3, 9, 82, 10] 배열을 수동으로 정렬하여 병합 정렬 알고리즘이 작동하는 방식을 살펴보겠습니다.

1단계: 나누기

병합 정렬의 첫 번째 단계는 배열을 하위 배열로 나눈 다음 모든 하위 배열에 항목이 하나만 남을 때까지 각 하위 배열을 하위 배열로, 하위 배열을 하위 배열로 나누는 것입니다.

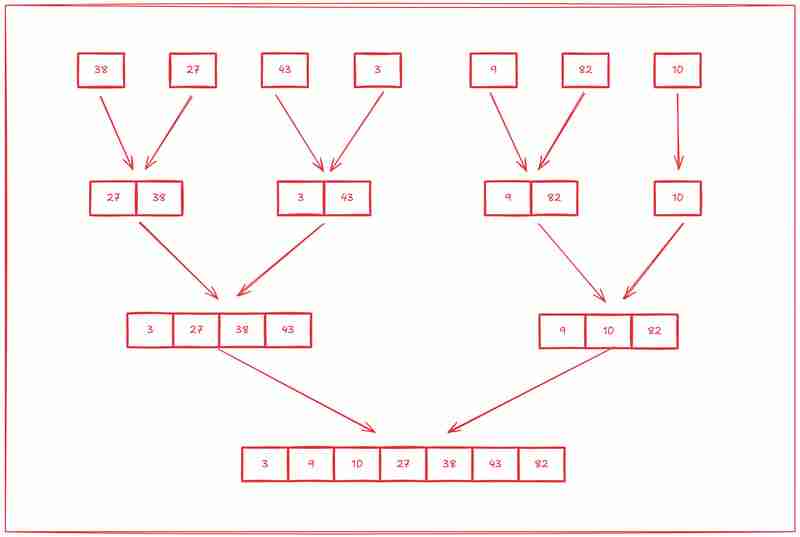
2단계: 다시 병합(정복)

두 번째 단계는 해당 하위 배열을 처음부터 정렬하는 것입니다.

시간 복잡도

병합 정렬은 모든 경우(최적, 평균, 최악)에서 O(n log n) 시간 복잡도를 달성하므로 더 큰 데이터 세트의 경우 O(n²) 알고리즘보다 더 효율적입니다.

이유는 다음과 같습니다.

• 나누기: 배열을 log n 번 나눕니다(각 나눗셈은 크기를 절반으로 줄입니다)
• 병합: 각 병합 수준에는 n개의 작업이 필요합니다
• 합계: n개 작업 × log n 수준 = O(n log n)

비교:

• 버블 정렬: O(n²)
• 선택 정렬: O(n²)
• 병합 정렬: O(n log n)

1,000개 요소 배열의 경우:

• O(n²) ≒ 1,000,000회 작업
• O(n log n) ≒ 10,000 연산

공간 복잡도

병합 정렬에는 병합 중에 임시 배열을 저장하기 위해 O(n)개의 추가 공간이 필요합니다. 이는 버블 정렬 또는 선택 정렬에 필요한 O(1) 공간보다 크지만 시간 효율성으로 인해 일반적으로 실제로 이러한 절충안을 가치 있게 만듭니다.

JavaScript로 구현

// The Merge Helper Function
function merge(left, right) {
  const result = [];
  let leftIndex = 0;
  let rightIndex = 0;

  while (leftIndex < left.length && rightIndex < right.length) {
    if (left[leftIndex] <= right[rightIndex]) {
      result.push(left[leftIndex]);
      leftIndex++;
    } else {
      result.push(right[rightIndex]);
      rightIndex++;
    }
  }

  // Add remaining elements
  while (leftIndex < left.length) {
    result.push(left[leftIndex]);
    leftIndex++;
  }

  while (rightIndex < right.length) {
    result.push(right[rightIndex]);
    rightIndex++;
  }

  return result;
}

병합 기능 분석:

1. 기능 설정:

   const result = [];
   let leftIndex = 0;
   let rightIndex = 0;

• 병합된 결과를 저장할 빈 배열을 만듭니다
• 두 입력 배열 모두에 대한 포인터를 초기화합니다
• 이러한 포인터는 각 배열의 위치를 ​​추적하는 손가락과 같다고 생각하세요

1. 주요 병합 논리:

   while (leftIndex < left.length && rightIndex < right.length) {
     if (left[leftIndex] <= right[rightIndex]) {
       result.push(left[leftIndex]);
       leftIndex++;
     } else {
       result.push(right[rightIndex]);
       rightIndex++;
     }
   }

• 두 배열의 요소를 비교합니다
• 더 작은 요소를 가져와서 결과에 추가합니다
• 우리가 가져온 배열에서 포인터를 앞으로 이동합니다
• 덱을 정렬할 때 두 장의 카드 중 작은 것을 선택하는 것처럼

1. 정리 단계:

   while (leftIndex < left.length) {
     result.push(left[leftIndex]);
     leftIndex++;
   }

• 나머지 요소 추가
• 한 배열이 다른 배열보다 길 수 있으므로 필요합니다
• 비교해서 남은 카드 모으듯

주요 병합 정렬 기능

function mergeSort(arr) {
  // Base case
  if (arr.length <= 1) {
    return arr;
  }

  // Divide
  const middle = Math.floor(arr.length / 2);
  const left = arr.slice(0, middle);
  const right = arr.slice(middle);

  // Conquer and Combine
  return merge(mergeSort(left), mergeSort(right));
}

병합 정렬 분석:

1. 기본 사례:

   if (arr.length <= 1) {
     return arr;
   }

• 길이가 0 또는 1인 배열을 처리합니다
• 정의에 따라 이미 정렬되어 있습니다
• 재귀 중지 지점 역할을 합니다

1. 분할 단계:

   const middle = Math.floor(arr.length / 2);
   const left = arr.slice(0, middle);
   const right = arr.slice(middle);

• 배열을 두 부분으로 분할
• Slice()는 원본을 수정하지 않고 새 배열을 생성합니다
• 카드 한 벌을 반으로 자르는 것과 같습니다

1. 재귀 정렬 및 병합:

   return merge(mergeSort(left), mergeSort(right));

• 각 절반을 재귀적으로 정렬
• 병합 기능을 사용하여 정렬된 절반을 결합
• 작은 카드 더미를 결합하기 전에 정렬하는 것과 같습니다

예제 연습

[38, 27, 43, 3]이 어떻게 정렬되는지 살펴보겠습니다.

1. 첫 번째 분할:

// The Merge Helper Function
function merge(left, right) {
  const result = [];
  let leftIndex = 0;
  let rightIndex = 0;

  while (leftIndex < left.length && rightIndex < right.length) {
    if (left[leftIndex] <= right[rightIndex]) {
      result.push(left[leftIndex]);
      leftIndex++;
    } else {
      result.push(right[rightIndex]);
      rightIndex++;
    }
  }

  // Add remaining elements
  while (leftIndex < left.length) {
    result.push(left[leftIndex]);
    leftIndex++;
  }

  while (rightIndex < right.length) {
    result.push(right[rightIndex]);
    rightIndex++;
  }

  return result;
}

1. 두 번째 분할:

   const result = [];
   let leftIndex = 0;
   let rightIndex = 0;

1. 뒤로 병합:

   while (leftIndex < left.length && rightIndex < right.length) {
     if (left[leftIndex] <= right[rightIndex]) {
       result.push(left[leftIndex]);
       leftIndex++;
     } else {
       result.push(right[rightIndex]);
       rightIndex++;
     }
   }

결론

병합 정렬은 대규모 데이터 세트에서 일관되게 좋은 성능을 발휘하는 매우 효율적인 정렬 알고리즘입니다. 단순한 정렬 알고리즘에 비해 추가 공간이 필요하지만 O(n log n) 시간 복잡성으로 인해 성능이 중요한 많은 실제 애플리케이션에 적합합니다.

주요 내용:

• 분할 정복 전략을 사용합니다
• 모든 경우에 O(n log n) 시간 복잡도
• O(n) 추가 공간 필요
• 안정적인 정렬 알고리즘
• 대규모 데이터세트에 적합

---

---

최신 소식과 연결 상태를 유지하세요

이 시리즈의 모든 부분을 놓치지 않도록 하고 저와 더 깊이 있게 소통하기 위해
소프트웨어 개발(웹, 서버, 모바일 또는 스크래핑/자동화), 데이터에 대한 토론
구조와 알고리즘, 기타 흥미로운 기술 주제에 대해 알아보려면 저를 팔로우하세요.

에마누엘 아인데 팔로우

소프트웨어 엔지니어 | 기술 작가 | 백엔드, 웹 및 모바일 개발자 ? | 효율적이고 확장 가능한 소프트웨어 솔루션 제작에 열정을 갖고 있습니다. #연결하자 ?

• 깃허브
• 링크드인
• 엑스(트위터)

앞으로 계속 지켜봐 주시기 바랍니다. 즐거운 코딩 되세요 ?‍??

위 내용은 병합 정렬 알고리즘 이해: 정렬 알고리즘 마스터를 위한 초보자 가이드의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!