집 >백엔드 개발 >파이썬 튜토리얼 >numpy&#s einsum의 불합리한 유용성

numpy&#s einsum의 불합리한 유용성

Patricia Arquette원래의: 2024-11-04 07:15:02200검색

소개

파이썬에서 가장 유용한 메소드인 np.einsum을 소개하겠습니다. np.einsum(및 Tensorflow 및 JAX의 대응 항목)을 사용하면 복잡한 행렬과 텐서 연산을 매우 명확하고 간결하게 작성할 수 있습니다. 또한 그 명확성과 간결함이 텐서 작업에 따른 정신적 과부하를 많이 덜어준다는 사실도 발견했습니다. 그리고 실제로 배우고 사용하는 것은 매우 간단합니다. 작동 방식은 다음과 같습니다. np.einsum에는 아래 첨자 문자열 인수가 있고 하나 이상의 피연산자가 있습니다.

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

subscripts 인수는 numpy에 피연산자의 축을 조작하고 결합하는 방법을 알려주는 "미니 언어"입니다. 처음에는 읽기가 조금 어렵지만, 익숙해지면 나쁘지 않습니다.

단일 피연산자

첫 번째 예에서는 np.einsum을 사용하여 행렬 A의 축을 교환합니다(일명 전치 사용).

M = np.einsum('ij->ji', A)

문자 i와 j는 A의 첫 번째와 두 번째 축에 바인딩됩니다. Numpy는 문자를 나타나는 순서대로 축에 바인딩하지만 numpy는 명시적인 경우 어떤 문자를 사용하든 상관하지 않습니다. 예를 들어 a와 b를 사용할 수 있으며 동일한 방식으로 작동합니다.

M = np.einsum('ab->ba', A)

그러나 반드시 피연산자에 있는 축 수만큼의 문자를 제공해야 합니다. A에는 두 개의 축이 있으므로 두 개의 서로 다른 문자를 제공해야 합니다. 다음 예는 첨자 수식에 바인딩할 문자가 하나뿐이므로 작동하지 않습니다. i:

# broken
M = np.einsum('i->i', A)

반면에 피연산자에 실제로 하나의 축만 있는 경우(i.o.w., 벡터임) 단일 문자 아래 첨자 수식은 잘 작동하지만 벡터를 a로 남겨두기 때문에 그다지 유용하지는 않습니다. 있는 그대로:

m = np.einsum('i->i', a)

축에 대한 합산

그런데 이 작전은 어떻습니까? 오른쪽에는 i가 없습니다. 이것이 유효한가요?

c = np.einsum('i->', a)

놀랍게도 그렇습니다! np.einsum의 본질을 이해하는 첫 번째 열쇠는 다음과 같습니다. 오른쪽에서 축을 생략하면 해당 축이 합계됩니다. The Unreasonable Usefulness of numpy

코드:

c = 0
I = len(a)
for i in range(I):
   c += a[i]

합산 동작은 단일 축으로 제한되지 않습니다. 예를 들어 아래 첨자 수식 c = np.einsum('ij->', A):을 사용하여 한 번에 두 축에 대한 합을 계산할 수 있습니다. The Unreasonable Usefulness of numpy

다음은 두 축에 대한 해당 Python 코드입니다.

c = 0
I,J = A.shape
for i in range(I):
   for j in range(J):
      c += A[i,j]

그러나 여기서 끝나지 않습니다. 창의력을 발휘하여 일부 축을 합산하고 다른 축은 그대로 둘 수 있습니다. 예를 들어, np.einsum('ij->i', A)는 행렬 A의 행을 합산하여 길이가 j인 행 합으로 구성된 벡터를 남깁니다. The Unreasonable Usefulness of numpy

코드:

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

마찬가지로 np.einsum('ij->j', A)는 A의 열을 합산합니다. The Unreasonable Usefulness of numpy

코드:

M = np.einsum('ij->ji', A)

두 개의 피연산자

단일 피연산자로 수행할 수 있는 작업에는 제한이 있습니다. 두 개의 피연산자를 사용하면 상황이 훨씬 더 흥미롭고 유용해집니다. 두 개의 벡터 a = [a_1, a_2, ... ] 및 b = [a_1, a_2, ...]이 있다고 가정해 보겠습니다. len(a) === len(b)인 경우 다음과 같이 내부 곱(내적이라고도 함)을 계산할 수 있습니다.

M = np.einsum('ab->ba', A)

여기에서는 두 가지 일이 동시에 일어나고 있습니다.

i는 a와 b 모두에 바인딩되어 있으므로 a와 b는 "일렬로 정렬"된 다음 함께 곱해집니다: a[i] * b[i].
우측에서 인덱스 i가 제외되었기 때문에 이를 제거하기 위해 축 i를 합산합니다.

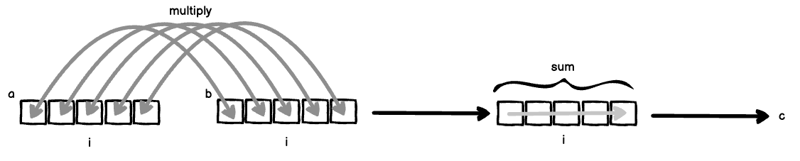
(1)과 (2)를 합치면 클래식한 내적이 나옵니다. The Unreasonable Usefulness of numpy

코드:

# broken
M = np.einsum('i->i', A)

이제, 아래 첨자 수식에서 i를 생략하지 않았다고 가정해 보겠습니다. 모든 a[i]와 b[i]를 곱하고 i에 대한 합을 곱하지 않습니다.

m = np.einsum('i->i', a)

코드:

c = np.einsum('i->', a)

이는 요소별 곱셈(또는 행렬의 Hadamard 곱)이라고도 하며 일반적으로 numpy 메서드 np.multiply를 통해 수행됩니다. 외적이라고 불리는 첨자 공식의 세 번째 변형이 아직 있습니다.

c = 0
I = len(a)
for i in range(I):
   c += a[i]

이 첨자 수식에서 a와 b의 축은 별도의 문자로 바인딩되므로 별도의 "루프 변수"로 처리됩니다. 따라서 C에는 모든 i와 j에 대한 항목 a[i] * b[j]가 행렬로 배열되어 있습니다. The Unreasonable Usefulness of numpy

코드:

c = 0
I,J = A.shape
for i in range(I):
   for j in range(J):
      c += A[i,j]

세 개의 피연산자

외부 제품에서 한 단계 더 나아가 피연산자 3개 버전은 다음과 같습니다.

I,J = A.shape
r = np.zeros(I)
for i in range(I):
   for j in range(J):
      r[i] += A[i,j]

3개의 피연산자 외부 곱에 해당하는 Python 코드는 다음과 같습니다.

I,J = A.shape
r = np.zeros(J)
for i in range(I):
   for j in range(J):
      r[j] += A[i,j]

더 나아가서 축의 오른쪽에 ik 대신 ki를 써서 결과를 전치하는 것 외에도 축을 합산하기 위해 축을 생략하는 것을 막을 수는 없습니다. ->:

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

동등한 Python 코드는 다음과 같습니다.

M = np.einsum('ij->ji', A)

이제 복잡한 텐서 연산을 보다 쉽게 지정하는 방법을 알아볼 수 있기를 바랍니다. numpy를 더 광범위하게 사용하면서 복잡한 텐서 연산을 구현해야 할 때마다 np.einsum에 도달하게 되었습니다. 내 경험상 np.einsum을 사용하면 나중에 코드를 더 쉽게 읽을 수 있습니다. 아래 첨자에서 바로 위의 연산을 쉽게 읽을 수 있습니다. "가운데 축을 합산하고 최종 결과를 전치한 세 벡터의 외부 곱입니다. ". 복잡한 일련의 연산을 읽어야 한다면 혀가 막힐 수도 있습니다.

실제적인 예

실용적인 예를 들어, 고전 논문 "Attention is All You Need"에 있는 LLM의 핵심 방정식을 구현해 보겠습니다. Eq. 1은 주의 메커니즘을 설명합니다. The Unreasonable Usefulness of numpy

이 용어에 집중하겠습니다

Q K^{T} QK^T

, 소프트맥스는 np.einsum 및 배율 인수로 계산할 수 없기 때문입니다.

\frac{1}{\sqrt{d_{k}}} frac{1}{sqrt{d_k}}

신청하기가 쉽지 않습니다.

$Q K^{T} QK^T$ 용어는 n 키를 사용하여 m 쿼리의 내적을 나타냅니다. Q는 m개의 d차원 행 벡터를 행렬로 쌓은 모음이므로 Q의 모양은 md입니다. 마찬가지로 K는 n개의 d차원 행 벡터가 행렬로 쌓인 집합이므로 K는 md 모양을 갖습니다.

단일 Q와 K 사이의 곱은 다음과 같이 작성됩니다.

np.einsum('md,nd->mn', Q, K)

아래 첨자 방정식을 작성하는 방식으로 인해 행렬 곱셈 전에 K를 전치할 필요가 없습니다!

The Unreasonable Usefulness of numpy

매우 간단해 보입니다. 사실 이는 전통적인 행렬 곱셈일 뿐입니다. 그러나 아직 끝나지 않았습니다. Attention Is All You Need는 다중 헤드 어텐션을 사용합니다. 이는 실제로 k개의 행렬 곱셈이 Q 행렬과 K 행렬의 인덱스 모음에서 동시에 발생한다는 것을 의미합니다. .

좀 더 명확하게 하기 위해 제품을 다음과 같이 다시 작성할 수도 있습니다. $Q_{i} K_{i}^{ㄷ} Q_iK_i^T$ .

즉, Q와 K 모두에 추가 축 i가 있다는 뜻입니다.

게다가 훈련 환경에 있다면 아마도 이러한 다중 방향 주의 작업을 일괄 실행하고 있을 것입니다.

아마도 배치 축을 따라 배치 예제에 대해 작업을 수행하고 싶을 것입니다. b. 따라서 전체 제품은 다음과 같습니다.

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

여기에서는 4축 텐서를 다루기 때문에 다이어그램을 건너뛰겠습니다. 하지만 이전 다이어그램을 "스택"하여 다중 헤드 축 i를 얻은 다음 해당 "스택"을 "스택"하여 배치 축 b를 얻는 것을 상상할 수 있습니다.

다른 numpy 메서드를 조합하여 이러한 작업을 어떻게 구현하는지 이해하기 어렵습니다. 그러나 조금만 살펴보면 무슨 일이 일어나고 있는지 명확합니다. 배치에 대해, 행렬 Q와 K의 모음에 대해 행렬 곱셈 Qt(K)를 수행합니다.

이제 정말 멋지지 않나요?

뻔뻔한 플러그

1년 동안 창업자 모드 그라인드를 한 후 일자리를 찾고 있습니다. 저는 다양한 기술 분야와 프로그래밍 언어에서 15년 이상의 경험을 갖고 있으며 팀 관리 경험도 있습니다. 수학과 통계는 중점 분야입니다. DM으로 이야기 나눠보세요!

위 내용은 numpy&#s einsum의 불합리한 유용성의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

Python qt batch numpy String if for math using Length Collection len this tensorflow

성명：

이전 기사：Pandas 집계 결과에서 과학적 표기법을 억제하는 방법은 무엇입니까?다음 기사：Pandas 집계 결과에서 과학적 표기법을 억제하는 방법은 무엇입니까?