두 포인트 그룹을 연결하는 데 필요한 최소 비용

1595. 두 포인트 그룹을 연결하는 데 필요한 최소 비용

난이도:어려움

주제: 배열, 동적 프로그래밍, 비트 조작, 매트릭스, 비트마스크

첫 번째 그룹은 크기₁점, 두 번째 그룹은 크기₂점, 크기₁ > = 크기₂.

두 점 사이의 연결 비용은 크기₁ x 크기₂ 행렬로 제공됩니다. 여기서 비용[i][j]는 점 i를 연결하는 비용입니다. 첫 번째 그룹과 두 번째 그룹의 점 j. 두 그룹의 각 포인트가 반대 그룹의 하나 이상의 포인트에 연결되면 그룹이 연결됩니다. 즉, 첫 번째 그룹의 각 점은 두 번째 그룹의 점 중 적어도 하나와 연결되어야 하고, 두 번째 그룹의 각 점은 첫 번째 그룹의 점 중 적어도 하나와 연결되어야 합니다.

두 그룹을 연결하는 데 필요한 최소 비용을 반환합니다.

예 1:

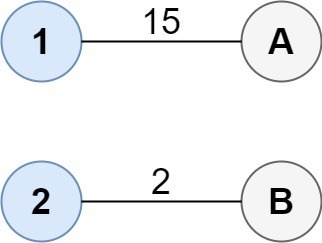
• 입력: 비용 = [[15, 96], [36, 2]]
• 출력: 17
• 설명: 그룹을 연결하는 최적의 방법은 다음과 같습니다.

  1--A
  2--B
  This results in a total cost of 17.

예 2:

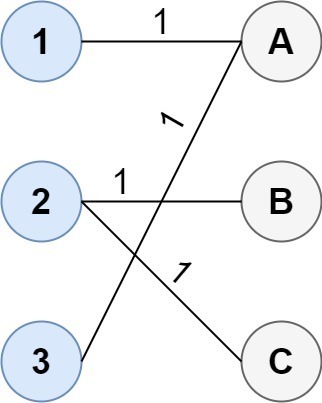
• 입력: 비용 = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
• 출력: 4
• 설명: 그룹을 연결하는 최적의 방법은 다음과 같습니다.

  1--A
  2--B
  2--C
  3--A
  This results in a total cost of 4.

첫 번째 그룹의 점 2와 두 번째 그룹의 점 A에 여러 개의 점이 연결되어 있습니다. 연결할 수 있는 포인트 수에는 제한이 없으므로 이는 중요하지 않습니다. 우리는 최소한의 총 비용만을 고려합니다.

예 3:

• 입력: 비용 = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8] ]
• 출력: 10

제약조건:

• 크기₁ == 비용.길이
• 크기₂ == 비용[i].길이
• 1 <= 사이즈₁, 사이즈₂ <= 12
• 크기₁ >= 크기₂
• 0 <= 비용[i][j] <= 100

힌트:

1. 왼쪽의 각 점은 이미 왼쪽 노드에 연결된 정확한 점에 연결되거나 어떤 노드에도 연결되지 않은 오른쪽 노드의 하위 집합에 연결됩니다.
2. 비트마스킹과 함께 동적 프로그래밍을 사용합니다. 여기서 상태는 (첫 번째 그룹에 할당된 포인트 수, 두 번째 그룹에 할당된 포인트의 비트마스크)입니다.

해결책:

비트마스킹을 통해 동적 프로그래밍을 활용할 수 있습니다. 첫 번째 그룹의 각 포인트를 고려하고 이를 두 번째 그룹의 모든 포인트에 연결하려고 노력하여 비용을 최소화한다는 아이디어입니다.

비트마스킹을 사용한 DP(동적 프로그래밍) 접근 방식

단계:

1. 주 대표:

   • 다음과 같은 경우 DP 테이블 dp[i][mask]를 사용합니다.
     • i는 첫 번째 그룹(0부터 size1-1까지)의 인덱스입니다.
     • 마스크는 두 번째 그룹의 어느 지점이 연결되었는지 나타내는 비트마스크입니다.

2. 상태 전환:

   • 첫 번째 그룹의 각 점에 대해 두 번째 그룹의 모든 점에 연결하고 이에 따라 DP 테이블을 업데이트해 보세요.
   • 두 번째 그룹의 새 포인트가 연결되면 마스크에서 해당 비트를 업데이트합니다.

3. 기본 사례:

   • dp[0][0] = 0으로 시작합니다(처음에는 연결 없음).

4. 목표:

   • 두 그룹의 모든 점 연결을 나타내는 dp[size1][(1 << size2) - 1]의 최소 비용을 계산합니다.

이 솔루션을 PHP: 1595로 구현해 보겠습니다. 두 포인트 그룹을 연결하는 데 필요한 최소 비용

  
  
  설명:



DP 배열 dp[i][mask]는 그룹 1의 첫 번째 i 지점을 마스크로 표시된 그룹 2의 지점과 연결하는 최소 비용을 저장합니다.
중첩 루프는 i와 마스크의 각 조합을 반복하여 가능한 모든 연결을 고려하여 최적의 비용을 찾으려고 노력합니다.
결국 솔루션은 두 번째 그룹의 일부 포인트가 아직 연결되지 않은 시나리오를 고려하여 최소 비용을 계산하여 모든 포인트가 연결되도록 합니다.


이러한 접근 방식은 문제의 제약을 효율적으로 처리하고 두 그룹을 연결하는 데 드는 비용을 최소화합니다.

연락처 링크
이 시리즈가 도움이 되었다면 GitHub에서 저장소에 별표를 표시하거나 즐겨찾는 소셜 네트워크에서 게시물을 공유해 보세요. 여러분의 지원은 저에게 큰 의미가 될 것입니다!

이렇게 더 유용한 콘텐츠를 원하시면 저를 팔로우해주세요.


링크드인
깃허브



          

            
        
위 내용은 두 포인트 그룹을 연결하는 데 필요한 최소 비용의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!