AVL 트리 자바

AVL 트리는 자체 균형 이진 트리라고도 알려져 있으며, 전체 균형 트리에서 결과가 둘 이상 나올 수 없는 왼쪽 및 오른쪽 하위 트리의 높이 차이를 계산하고 균형을 유지하는 데 사용됩니다. 이진 검색 트리 작업을 통해 AVL 트리의 일부로 필요한 삽입, 삭제, 검색, 최대 및 최소 작업도 가능합니다. 이러한 모든 작업은 비용이 많이 드는 작업으로 간주되므로 모든 BST의 높이 차이가 유지되면 이와 관련된 비용 및 시간 복잡성이 유지될 수 있습니다.

무료 소프트웨어 개발 과정 시작

웹 개발, 프로그래밍 언어, 소프트웨어 테스팅 등

구문:

이런 적절한 구문은 없지만 Java AVL 트리에서 구현하는 동안 구문은 다음과 같이 표현되는 데이터 구조로 간주됩니다.

Class Node_demo
{
int key, height_0;
Node left, right;
Node_demo (int d_1)
{
key = d_1;
height_0 = 1;
}
}
class AVLTree_demo1 {
Node root_0;
int height_0(Node N_1) {
if (N_1== null)
return 0;
return N_1.height;
}

설명:

여기 구문 흐름에서 Node_demo 클래스에는 요소가 저장될 키-값 쌍을 설명하는 키, 높이 및 구조가 포함되어 있습니다. 그 다음에는 루트 노드와 null 값으로 모든 위치에서 유지되는 높이를 갖는 값 쌍이 있는 관련 요소가 포함된 AVL_Tree 데모_1 노드가 이어집니다.

Java에서 AVL 트리는 어떻게 작동하나요?

• Java에서 AVL 트리가 작동하는 적절한 흐름이 존재하며 1962년 GM Adelson이 발명했습니다.
• AVL 트리는 각 노드가 왼쪽 하위 트리의 높이에서 오른쪽 하위 트리의 높이를 빼서 계산되는 균형 인자와 연관된 높이 균형 이진 검색 트리로 정의됩니다.
• 균형 요소가 -1에서 1 사이에 있으면 트리를 균형 잡힌 트리라고 합니다. 그렇지 않으면 트리는 위에서 아래로 균형을 이루어야 합니다.
• 균형 트리가 이진 검색 트리의 높이를 제어하므로 높이는 O(h)로 나오는 반면, 이진 검색 트리가 기울어지면 이 경우보다 확장해야 하는 조항이 있습니다. 조작의 경우 (n-1)로 나옵니다.
• 비뚤어진 트리가 제한되면 O(log n)로 나타나는 모든 작업에 상한이 적용됩니다. 여기서 n은 노드 수입니다.
• AVL 트리를 회전하는 방법도 있으며 이는 균형 요소가 -1, 1 또는 0 사이에 있는 한 가지 조건에서만 발생합니다.
• 회전에는 다음과 같은 4가지 유형이 있습니다.
• LL 회전: 노드가 노드 D가 있는 트리의 왼쪽 하위 트리에 있으면 노드가 삽입됩니다.
• RR 회전: 노드가 노드 D가 있는 트리의 오른쪽 하위 트리에 있으면 노드가 삽입됩니다.
• LR 회전: 노드 D가 있는 왼쪽 하위 트리의 오른쪽 하위 트리에 삽입되면 노드가 삽입됩니다.
• RL 회전: 노드 D가 있는 오른쪽 하위 트리의 왼쪽 하위 트리에 삽입되면 노드가 삽입됩니다.

D는 높이와 균형 요소가 -1, 1, 0이 아닌 노드를 의미하며, 이로 인해 올바른 형식을 만들기 위해 이러한 모든 회전이 필요합니다.

존재하는 연산이 많고 이를 위해서는 조작을 위한 적절한 분석과 함께 적절한 회전이 있어야 합니다.

예: 이 예는 아래 출력과 같이 선순, 후순 및 레벨 순서 표현을 사용하여 삽입, 왼쪽 및 오른쪽 삽입이 있는 AVL 트리를 보여줍니다.

import java. util.LinkedList;
import java.util.Queue;
class Node_8 {
int data_0, height_1;
Node_8 left_nd_0;
Node_8 right_nd_0;
Node_8(int d_2) {
data_0 = d_2;
height_1 = 1;
}
}
public class AVLTree_Demo
{
Node_8 root_0;
int height_1(Node_8 N) {
if (N == null)
return 0;
return N.height_1;
}
int max_2(int a_0,  int b_0) {
return (a_0 > b_0) ? a_0 : b_0;
}
Node_8 rightRotation_mode(Node_8 oldRoot_0) {
Node_8 newRoot_0 = oldRoot_0.left_nd_0;
Node_8 temp_0 = newRoot_0.right_nd_0;
newRoot_0.right_nd_0 = oldRoot_0;
oldRoot_0.left_nd_0 = temp_0;
newRoot_0.height_1 = max_2(height_1(newRoot_0.left_nd_0), height_1(newRoot_0.right_nd_0)) + 1;
oldRoot_0.height_1 = max_2(height_1(oldRoot_0.left_nd_0), height_1(oldRoot_0.right_nd_0)) + 1;
return newRoot_0;
}
Node_8 leftRotation_mode(Node_8 oldRoot_0) {
Node_8 newRoot_0 = oldRoot_0.right_nd_0;
Node_8 temp_0 = newRoot_0.left_nd_0;
newRoot_0.left_nd_0 = oldRoot_0;
oldRoot_0.right_nd_0 = temp_0;
newRoot_0.height_1 = max_2(height_1(newRoot_0.left_nd_0), height_1(newRoot_0.right_nd_0)) + 1;
oldRoot_0.height_1=max_2(height_1(oldRoot_0.left_nd_0), height_1(oldRoot_0.right_nd_0)) + 1;
return newRoot_0;
}
int balFactor_c(Node_8 root_0) {
if(root_0 == null)
return 0;
return height_1(root_0.left_nd_0) - height_1(root_0.right_nd_0);
}
Node_8 insert(Node_8 root_0, int data_0) {
if(root_0 == null)
return new Node_8(data_0);
else if(data_0 < root_0.data_0)
root_0.left_nd_0 = insert(root_0.left_nd_0, data_0);
else if(data_0 > root_0.data_0)
root_0.right_nd_0 = insert(root_0.right_nd_0, data_0);
else
return root_0;
root_0.height_1= max_2(height_1(root_0.left_nd_0), height_1(root_0.right_nd_0)) + 1;
int bal = balFactor_c(root_0);
if(bal > 1 && data_0 < root_0.left_nd_0.data_0)
return rightRotation_mode(root_0);
if(bal < -1 && data_0 > root_0.right_nd_0.data_0)
return leftRotation_mode(root_0);
if(bal > 1 && data_0 > root_0.left_nd_0.data_0) {
root_0.left_nd_0 = leftRotation_mode(root_0.left_nd_0);
return rightRotation_mode(root_0);
}
if(bal < -1 && data_0 < root_0.right_nd_0.data_0) {
root_0.right_nd_0 = rightRotation_mode(root_0.right_nd_0);
return leftRotation_mode(root_0);
}
return root_0;
}
void preOrder_traversal(Node_8 node) {
if (node != null) {
System.out.print(node.data_0 + " ");
preOrder_traversal(node.left_nd_0);
preOrder_traversal(node.right_nd_0);
}
}
void levelOrder_traversal(Node_8 root) {
Queue<Node_8> q_1 = new LinkedList<Node_8>();
q_1.add(root);
while(!q_1.isEmpty()) {
Node_8 current = q_1.peek();
System.out.print(current.data_0 + " ");
if(current.left_nd_0 != null)
q_1.add(current.left_nd_0);
if(current.right_nd_0 != null)
q_1.add(current.right_nd_0);
q_1.poll();
}
}
public static void main (String args[]) {
AVLTree_Demo tree = new AVLTree_Demo ();
tree. root_0 = tree.insert(tree.root_0, 15);
tree.root_0 = tree.insert(tree.root_0, 20);
tree.root_0 = tree.insert(tree.root_0, 19);
tree.root_0 = tree.insert(tree.root_0, 40);
tree.root_0 = tree.insert(tree.root_0, 50);
tree.root_0 = tree.insert(tree.root_0, 25);
System.out.println("order_of_Preorder_traversal_representation : ");
tree.preOrder_traversal(tree.root_0);
System.out.println();
System.out.println("Levelorder_of_traversal_representation : ");
tree.levelOrder_traversal(tree.root_0);
}
}

출력:

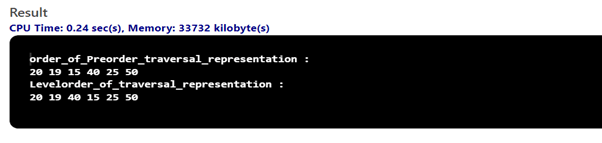
설명: 이 프로그램은 가져온 목록이 비어 있는지 여부와 AVL 트리에 선주문, 후주문 또는 레벨 순서 형식으로 회전이 수행됩니다. 제공된 모든 요소는 자동으로 입력을 받아 올바른 순서로 정렬됩니다.

결론

Java의 AVL 트리는 작업 측면에서 우위를 제공하고 대규모 코드 세트로 인해 발생하는 시간 복잡성을 절약하고 소비하는 데 도움이 되기 때문에 많은 개발자가 선호하는 적절한 데이터 구조로 사용됩니다. AVL 트리는 높이가 적절하게 유지되면 전체 하위 트리에서 삽입, 삭제, 회전, 제거와 같은 주요 작업을 처리할 수 있는 기능을 가지고 있습니다.

위 내용은 AVL 트리 자바의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!