Java의 정렬 알고리즘

종종 배열과 같은 프레임워크 내에서 특정 순서로 정보를 정렬하는 것은 정보를 배열하는 것입니다. 다양한 시퀀스 요구 사항을 사용할 수 있습니다. 인기 있는 방법은 숫자를 작은 것부터 큰 것까지 또는 그 반대로 정렬하거나 사전순으로 문자열을 정렬하는 것입니다. 정렬이 어떻게 작동하는지에 관심이 있는 경우 비효율적이지만 직관적인 대안부터 Java 및 기타 언어로 효과적으로 구현되는 효율적인 알고리즘에 이르기까지 다양한 알고리즘을 다룰 것입니다.

Java의 다양한 정렬 알고리즘

다양한 정렬 알고리즘이 있으며 모두가 똑같이 효과적인 것은 아닙니다. 이를 비교하고 어느 것이 가장 좋은지 확인하기 위해 시간 복잡성을 분석하겠습니다.

광고 이 카테고리에서 인기 있는 강좌 JAVA MASTERY - 전문 분야 | 78 코스 시리즈 | 15가지 모의고사

1. 삽입정렬
2. 버블정렬
3. 선택 정렬
4. 병합정렬
5. 힙정렬

1. 삽입정렬

삽입 정렬의 기본 개념은 범위를 정렬된 하위 배열과 정렬되지 않은 하위 배열로 나누는 것입니다. 분류된 부분은 기간 1의 시작 부분에 있으며 배열의 첫 번째(왼쪽) 구성 요소와 일치합니다. 우리는 배열을 통해 이동하고 매 반복마다 배열의 분류된 부분을 하나의 구성 요소씩 확장합니다. 확장할 때 정렬된 하위 배열에 새로운 요소를 배치합니다. 첫 번째 구성 요소를 변경할 필요가 없다는 것을 알 때까지 모든 요소를 ​​오른쪽으로 이동하여 이를 수행합니다. 굵은 글씨 부분을 오름차순으로 정렬하면 다음과 같은 배열이 발생합니다.

1. 3 5 7 8 4 2 1 9 6: 4를 고려하여 이것을 삽입하는 것이 우리에게 필요한 것입니다. 우리는 8 > 4
2. 2. 3 5 7 x 8 2 1 9 6
3. 3 5 x 7 8 2 1 9 6
4. 3 x 5 7 8 2 1 9 6
5. 3 4 5 7 8 2 1 9 6

코드:

public class InsertionSortEx {
public static void insertionSort(int[] arr) {
for (int x = 1; x < arr.length; x++) {
int current = arr[x];
int y = x - 1;
while(y >= 0 && current < arr[y]) {
arr[y+1] = arr[y];
y--;
}
arr[y+1] = current;
}
}
public static void main(String a[]){
int[] arr1 = {3,5,7,8,4,2,1,9,6};
System.out.println("Before Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
System.out.println();
insertionSort(arr1);//sorting array using insertion sort
System.out.println("After Insertion Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
}
}

출력:

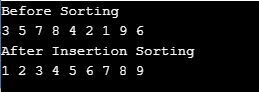
이 방법에 따라 하나의 구성 요소가 정렬된 부분을 확장했습니다. 이제 4개의 요소 대신 5개의 요소가 있습니다. 모든 반복이 이 작업을 수행하며 전체 배열은 끝을 기준으로 정렬됩니다.

참고: 이는 각 반복에서 전체 분류 목록을 하나씩 전송해야 하기 때문입니다(O(n)). 우리는 각 테이블의 각 구성 요소에 대해 이 작업을 수행해야 하며 이는 O(n^2) 제한이 있음을 의미합니다.2.

2. 버블정렬

버블이 필요한 순서대로 되지 않을 경우 주변 부품을 교체하여 작동됩니다. 이는 배열 시작부터 모든 구성 요소의 순서가 정해질 때까지 반복됩니다. 우리는 교체 없이 전체 반복을 수행할 수 있다면 인접한 요소와 비교된 모든 항목이 바람직한 순서, 더 나아가 전체 배열에 있다는 것을 알고 있습니다. Bubble Sort 알고리즘을 사용하는 이유는 숫자가 "바닥"으로 "거품처럼 솟아오르기" 때문입니다. 일정량 이후 다시 인스턴스를 진행하면(4가 좋은 인스턴스) 숫자가 천천히 오른쪽으로 이동하는 것을 확인할 수 있습니다.

버블 정렬 단계는 다음과 같습니다.

1. 4 21 5 3: 여기서 1^st 두 숫자의 순서가 올바르지 않습니다. 따라서 두 숫자를 모두 정렬해야 합니다.
2. 2 4 15 3: 그 다음 숫자 쌍도 올바른 순서가 아닙니다. 그래서 정렬이 다시 발생합니다.
3. 2 1 4 53: 이 두 가지는 올바른 순서로 되어 있습니다. 4 < 5이므로 교체할 필요가 없습니다.
4. 2 1 4 5 3: 이번에도 올바른 순서로 바꿔야 합니다.
5. 2 1 4 3 5: 한 번의 반복 후 결과 배열은 다음과 같습니다.
6. 숫자가 올바른 순서가 될 때까지 이 과정을 다시 반복해야 합니다.

코드:

public class BubbleSortExample {
public static void bubbleSort(int[] arr) {
int n = arr.length;
int tmp = 0;
for(int x=0; x < n; x++){
for(int y=1; y < (n-x); y++){
if(arr[y-1] > arr[y]){
//swap elements
tmp = arr[y-1];
arr[y-1] = arr[y];
arr[y] = tmp;
}
}
}
}
public static void main(String[] args) {
int arr[] ={4,2,1,5,3};
System.out.println("Array Before Bubble Sort");
for(int x=0; x < arr.length; x++){
System.out.print(arr[x] + " ");
}
System.out.println();
bubbleSort(arr);
System.out.println("Array After Bubble Sort");
for(int x=0; x < arr.length; x++){
System.out.print(arr[x] + " ");
}
}
}

출력:

참고: a[i]>= a[i+1 ]를 사용하면 해당 연결이 동등한 구성 요소와 여전히 유효하므로 항상 하나의 연결에서 교체하기 때문에 무한 루프에 빠질 수 있습니다. 요소를 다른 요소로.

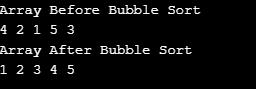
3. 선택 정렬

선택 정렬은 배열을 정렬되지 않은 분류 배열로 분할합니다. 그러나 이번에는 정렬 하위 배열이 스와핑을 통해 정렬되지 않은 하위 배열의 최소 요소를 정렬된 배열의 끝에 삽입하여 형성됩니다.

1. 3 5 12 4
2. 15 3 2 4
3. 1 23 5 4
4. 1 2 35 4
5. 1 2 3 45
6. 1 2 3 4 5

코드:

public class SelectionSortEx {
public static void selectionSort(int[] arr){
for (int x = 0; x < arr.length - 1; x++)
{
int indx = x;
for (int y = x + 1; y < arr.length; y++){
if (arr[y] < arr[indx]){
indx = y;
}
}
int smallNumber = arr[indx];
arr[indx] = arr[x];
arr[x] = smallNumber;
}
}
public static void main(String a[]){
int[] arr1 = {3,5,1,2,4};
System.out.println("Before Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
System.out.println();
selectionSort(arr1);
System.out.println("After Selection Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
}
}

출력:

Note: The minimum is O(n) for the array size because all the components must be checked. For each element of the array, we must find the minimum and make the whole process O (n^2) limited.

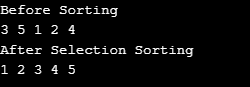
4. Merge Sort

Merge Sort utilizes recursion to fix the issue of the divide and conquest method more effectively than earlier described algorithms.

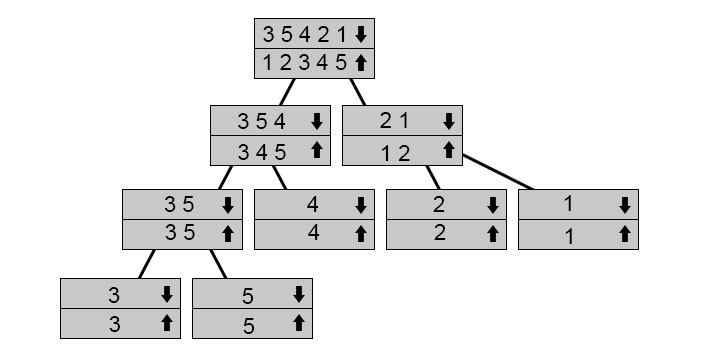
This tree shows how the recursive calls function. Down arrow marked arrays are the arrays for which we call function while we fuse up arrow arrays. Then you follow the arrow to the tree’s edge and then return and merge. We’ve got 3 5 3 1 range, so we split it into 3 5 4 and 2 1. We split them into their parts in order to sort them. We begin fusioning and sorting them as we go when we get to the bottom.

Code:

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
public class MergeSort {
static void merge(int[] array,int lowval,int midval,int highval){
int x, y ,k;
int[] c= new int[highval-lowval+1];
k = 0;
x=lowval;
y=midval+1;
while(x<=midval && y<=highval){
if(array[x]<=array[y]){
c[k++] = array[x++];
}
else{
c[k++] = array[y++];
}
}
while(x<=midval){
c[k++] = array[x++];
}
while(y<=highval){
c[k++] = array[y++];
}
k=0;
for(x = lowval; x<=highval; x++){
array[x] = c[k++];
}
}
static void mergeSort(int[] array,int lowval, int highval){
if(highval-lowval+1>1){
int midval = (lowval+highval)/2;
mergeSort(array,lowval,midval);
mergeSort(array,midval+1,highval);
merge(array,lowval,midval,highval);
}
}
public static void main(String[] args) {
BufferedReader r = new BufferedReader(new InputStreamReader(System.in));
int size;
System.out.println("Enter the array");
try {
size = Integer.parseInt(r.readLine());
} catch (Exception e) {
System.out.println("Please Enter valid Input");
return;
}
int[] array = new int[size];
System.out.println("Enter array elements");
int x;
for (x = 0; x < array.length; x++) {
try {
array[x] = Integer.parseInt(r.readLine());
} catch (Exception e) {
System.out.println("An error Occurred");
}
}
System.out.println("After Sorting");
System.out.println(Arrays.toString(array));
mergeSort(array,0,array.length-1);
System.out.println("Before Merge Sorting");
System.out.println(Arrays.toString(array));
}
}

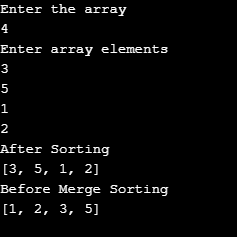
In this program, we have asked the user to enter input. The output will be in sorted order based on the user’s input.

Output:

5. Heap Sort

You first must know the framework on which Heapsort operates-the heap-in order to comprehend why it operates. We will specifically speak about a binary heap, but you can also generalize this to other heap constructions. A heap is a tree that fulfills the property of the heap, namely that all its kids have relationships to each node. A heap must also be nearly finished. A near-complete d-depth binary has a d-1 subtree with the same root, and each node has a full, left subtree, with a left descending.

In other words, you get a lower and lower number (min-heap) or larger and bigger (max-heap) when moving down the tree. Here is a max-heap instance:

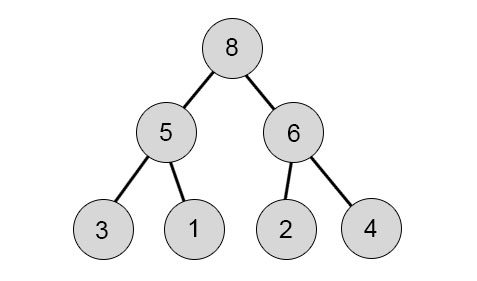
1. 6 1 8 3 5 2 4: Here, Both children’s numbers are smaller than the parent; hence we do not have to change anything.
2. 6 1 8 3 52 4: Here, 5 > 1, we need to swap them. We need to heapify for 5.
3. 6 5 8 3 12 4: Both of the children’s numbers are smaller; everything remains the same.
4. 6 5 83 1 2 4: Here, 8 > 6, hence we should swap them.
5. 8 5 6 3 1 2 4: After this iteration, we will get this result.

After Repeating this process again, we will get the following results:

• 8 5 6 3 1 2 4
1. 4 5 6 3 1 2 8: Swapping
2. 6 5 4 3 1 2 8: Heapify
3. 2 5 4 3 1 6 8: Swapping
4. 5 2 4 2 1 6 8: Heapify
5. 1 2 4 2 5 6 8: Swapping

Code:

public class HeapSort
{
public void sort(int arr[])
{
int n = arr.length;
for (int x = n / 2 - 1; x >= 0; x--)
heapify(arr, n, x);
for (int x=n-1; x>=0; x--)
int tmp = arr[0];
arr[0] = arr[x];
arr[x] = tmp;
heapify(arr, x, 0);
}
}
void heapify(int arr[], int n, int x)
{
int largest = x;
int L = 2*x + 1;
int r = 2*x + 2;
if (L < n && arr[L] > arr[largest])
largest = L;
if (r < n && arr[r] > arr[largest])
largest = r;
if (largest != x)
{
int swap = arr[x];
arr[x] = arr[largest];
arr[largest] = swap;
heapify(arr, n, largest);
}
}
static void printArray(int arr[])
{
int n = arr.length;
for (int x=0; x<n; ++x)
System.out.print(arr[x]+" ");
System.out.println();
}
public static void main(String args[])
{
int arr[] = {6,1,8,3,5,2,4};
int n = arr.length;
System.out.println("Before Sorting:");
printArray(arr);
HeapSort ob = new HeapSort();
ob.sort(arr);
System.out.println("After Heap Sorting:");
printArray(arr);
}
}

Output:



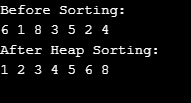
You can view it from point to level of the graph, from left to right. We achieved here that when we have the kth component in the array, the position of its children is 2\*k+1 and 2\*k+2 (assuming that indexing begins at 0). You can monitor this. The position of the parent is always (k-1)/2 for the kth component. You can readily “max heap up” any range because you know that. Check whether one of its kids is lower than that for each component. If so, pair one parent and repeat this step recursively with the parent.

Note: Since iterating for-loops across the entire array makes heapSort) (obviously O(N), it would create Heapsort O’s overall complexity(nlog n). Heapsort has an on-the-spot type, which means that it requires O(1) more room than Merge Sort, but it has some disadvantages, such as parallels that are hard.

Conclusion – Sorting Algorithms in Java

Sorting is a very prevalent procedure with datasets, whether for further analysis, speeding search with more effective algorithms relying on sorted information, filtering information, etc. Several languages endorse sorting, and often the interfaces obscure what the programmer does.

위 내용은 Java의 정렬 알고리즘의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!