최대 확률의 경로
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB원래의
- 2024-08-28 06:40:37770검색
1514. 최대 확률의 경로
난이도:중
주제: 배열, 그래프, 힙(우선순위 대기열), 최단 경로
n개 노드(0-인덱스)의 무방향 가중치 그래프가 제공됩니다. 이는 간선 목록으로 표시됩니다. 여기서 edge[i] = [a, b]는 노드 a와 b를 성공 확률로 연결하는 무방향 간선입니다. 그 가장자리를 횡단하는 것 succProb[i].
두 노드의 시작과 끝이 주어지면 처음부터 끝까지 성공 확률이 최대인 경로를 찾아 성공 확률을 반환합니다.
처음부터 끝까지 경로가 없으면 0을 반환합니다. 귀하의 답변은 정답과 최대 1e-5만큼 다를 경우 승인됩니다.
예 1:
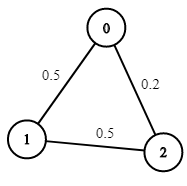
- 입력: n = 3, 가장자리 = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], 시작 = 0, 끝 = 2
- 출력: 0.25000
- 설명: 처음부터 끝까지 두 가지 경로가 있습니다. 하나는 성공 확률 = 0.2이고 다른 하나는 0.5 * 0.5 = 0.25입니다.
예 2:
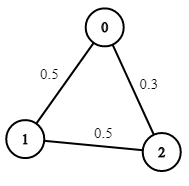
- 입력: n = 3, 가장자리 = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], 시작 = 0, 끝 = 2
- 출력: 0.30000
예 3:
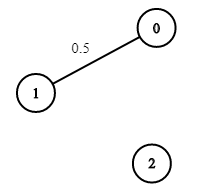
- 입력: n = 3, 가장자리 = [[0,1]], succProb = [0.5], 시작 = 0, 끝 = 2
- 출력: 0.00000
- 설명: 0과 2 사이에는 경로가 없습니다.
제약조건:
- 2
- 0 <= 시작, 끝 < ㄴ
- 시작 != 끝
- 0 <= a, b < ㄴ
- a !=b
- 0 <= succProb.length == edge.length <= 2*10^4
- 0 <= succProb[i] <= 1
- 두 노드 사이에는 최대 하나의 간선이 있습니다
힌트:
- 확률을 곱하면 정밀도 오류가 발생합니다.
- 숫자를 곱하는 대신 로그 확률을 사용하여 숫자를 합산하세요.
- Dijkstra의 알고리즘을 사용하여 모든 비용을 무효화한 후 두 노드 사이의 최소 경로를 찾습니다.
해결책:
Dijkstra 알고리즘의 수정된 버전을 사용할 수 있습니다. 최단 경로를 찾는 것이 아니라 성공 확률을 극대화하게 됩니다.
이 솔루션을 PHP로 구현해 보겠습니다: 1514. 최대 확률의 경로
<?php
/**
* @param Integer $n
* @param Integer[][] $edges
* @param Float[] $succProb
* @param Integer $start_node
* @param Integer $end_node
* @return Float
*/
function maxProbability($n, $edges, $succProb, $start_node, $end_node) {
...
...
...
/**
* go to ./solution.php
*/
}
// Example usage:
$n1 = 3;
$edges1 = [[0,1],[1,2],[0,2]];
$succProb1 = [0.5,0.5,0.2];
$start_node1 = 0;
$end_node1 = 2;
echo maxProbability($n1, $edges1, $succProb1, $start_node1, $end_node1);//Output: 0.25000
$n2 = 3;
$edges2 = [[0,1],[1,2],[0,2]];
$succProb2 = [0.5,0.5,0.3];
$start_node2 = 0;
$end_node2 = 2;
echo maxProbability($n2, $edges2, $succProb2, $start_node2, $end_node2);//Output: 0.30000
$n3 = 3;
$edges3 = [[0,1]];
$succProb3 = [0.5;
$start_node3 = 0;
$end_node3 = 2;
echo maxProbability($n3, $edges3, $succProb3, $start_node3, $end_node3); //Output: 0.00000
?>
<h3>
설명:
</h3>
<ol>
<li><p><strong>그래프 표현</strong>: 그래프는 각 노드가 이웃을 가리키는 인접 목록과 이를 연결하는 에지의 성공 확률로 표현됩니다.</p></li>
<li><p><strong>최대 확률 배열</strong>: 배열 maxProb는 시작 노드에서 각 노드에 도달할 최대 확률을 저장하는 데 사용됩니다.</p></li>
<li><p><strong>우선순위 큐</strong>: 최대 힙(SplPriorityQueue)은 확률이 가장 높은 경로를 먼저 탐색하는 데 사용됩니다. 이는 목적지 노드에 도달했을 때 최대 확률로 경로를 찾았는지 확인하는 데 중요합니다.</p></li>
<li>
<p><strong>알고리즘</strong>:</p>
<ul>
<li>시작 노드의 확률을 1로 초기화합니다(시작에 머무를 확률은 1이므로).</li>
<li>우선순위 대기열을 사용하여 노드를 탐색하고 각 이웃에 도달할 수 있는 최대 확률을 업데이트합니다.</li>
<li>목적지 노드에 도달하면 확률을 반환합니다.</li>
<li>경로가 없으면 0을 반환합니다.</li>
</ul>
</li>
</ol>
<h3>
산출:
</h3>
<p>제공된 예:<br>
</p>
<pre class="brush:php;toolbar:false">$n = 3;
$edges = [[0,1],[1,2],[0,2]];
$succProb = [0.5,0.5,0.2];
$start_node = 0;
$end_node = 2;
출력은 0.25가 됩니다.
이 접근 방식은 확률 계산의 세부 사항을 처리하면서 Dijkstra 알고리즘을 사용하여 효율적인 솔루션을 보장합니다.
연락처 링크
이 시리즈가 도움이 되었다면 GitHub에서 저장소에 별표를 표시하거나 즐겨찾는 소셜 네트워크에서 게시물을 공유해 보세요. 여러분의 지원은 저에게 큰 의미가 될 것입니다!
이렇게 더 유용한 콘텐츠를 원하시면 저를 팔로우해주세요.
- 링크드인
- 깃허브
위 내용은 최대 확률의 경로의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
성명:
본 글의 내용은 네티즌들의 자발적인 기여로 작성되었으며, 저작권은 원저작자에게 있습니다. 본 사이트는 이에 상응하는 법적 책임을 지지 않습니다. 표절이나 침해가 의심되는 콘텐츠를 발견한 경우 admin@php.cn으로 문의하세요.

