선 생성을 배울 때 왜 행렬과 그래프 사이에 등가 관계가 있는지 몰랐나요?

행렬은 이해하기 어렵지만 다른 관점에서는 다를 수 있습니다.

수학을 배울 때 우리는 배우는 지식의 난이도와 추상성 때문에 좌절할 때가 많지만, 때로는 관점을 바꾸는 것만으로도 문제에 대한 간단하고 직관적인 해결책을 찾을 수 있습니다. 예를 들어, 우리가 어렸을 때 제곱합 (a+b)² 공식을 배울 때 그것이 왜 a²+2ab+b²와 같은지 이해하지 못할 수도 있습니다. 책을 읽고 선생님이 이것을 이렇게 기억하라고 하셨습니다. 언젠가 우리가 볼 때까지 나는 이 애니메이션 그림을 보았습니다:

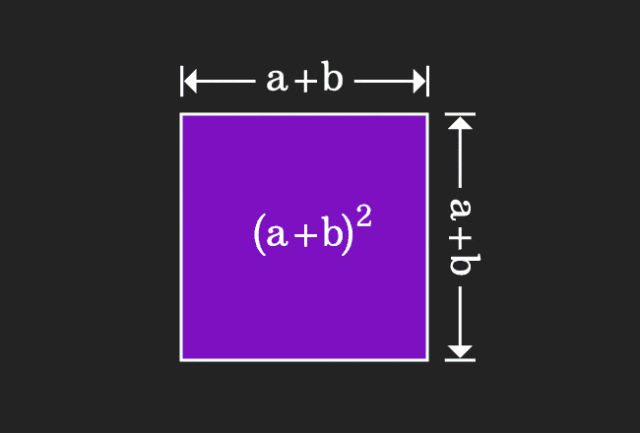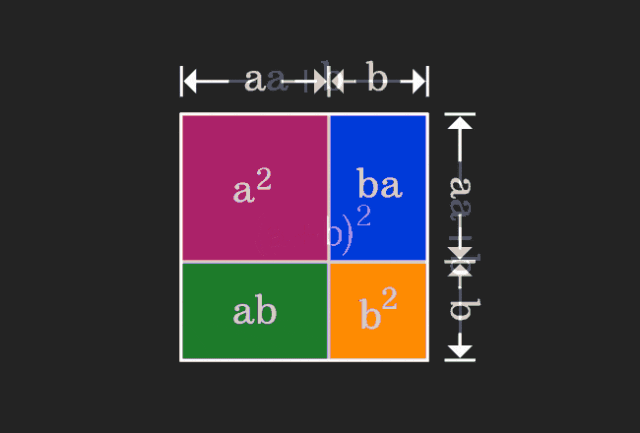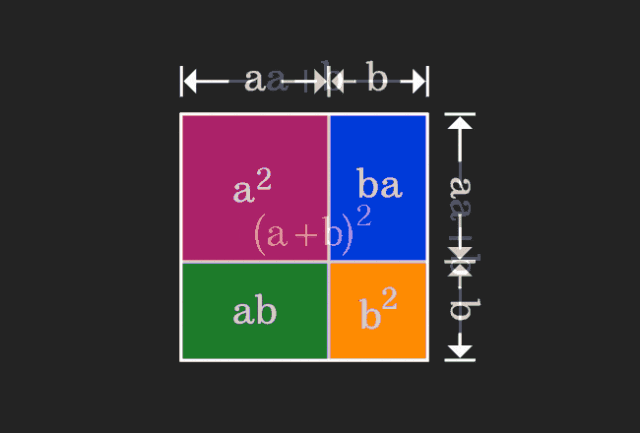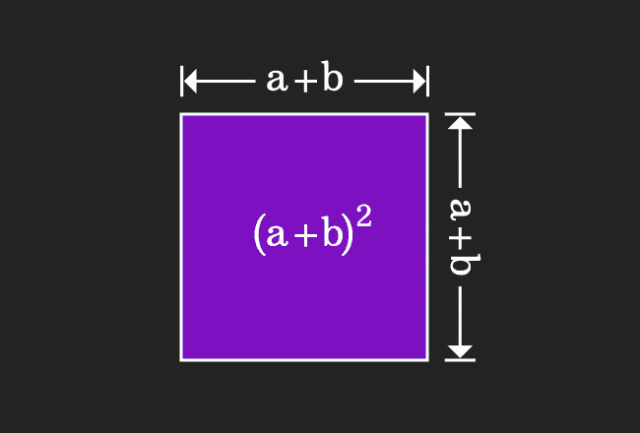
나는 갑자기 우리가 기하학적 관점에서 그것을 이해할 수 있다는 것을 깨달았습니다!

이제 깨달음의 의미가 다시 나타납니다. 음수가 아닌 행렬은 해당 유향 그래프로 동등하게 변환될 수 있습니다!

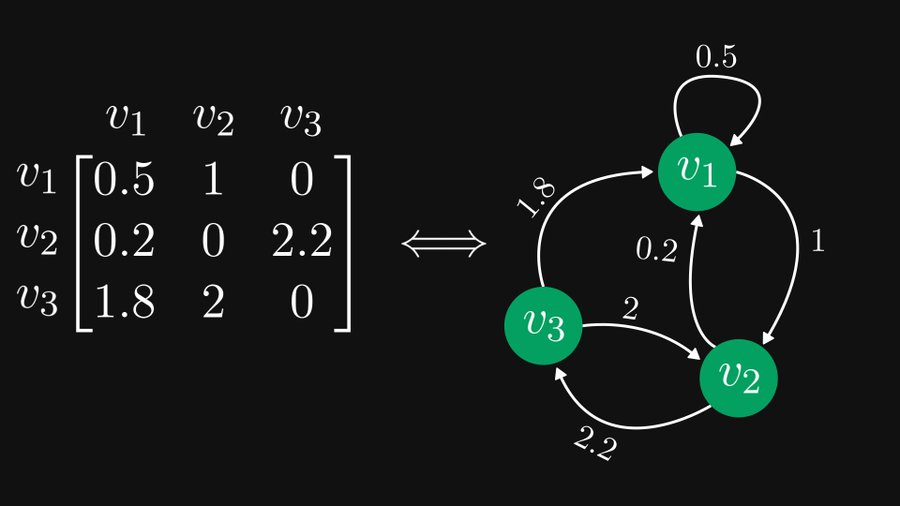
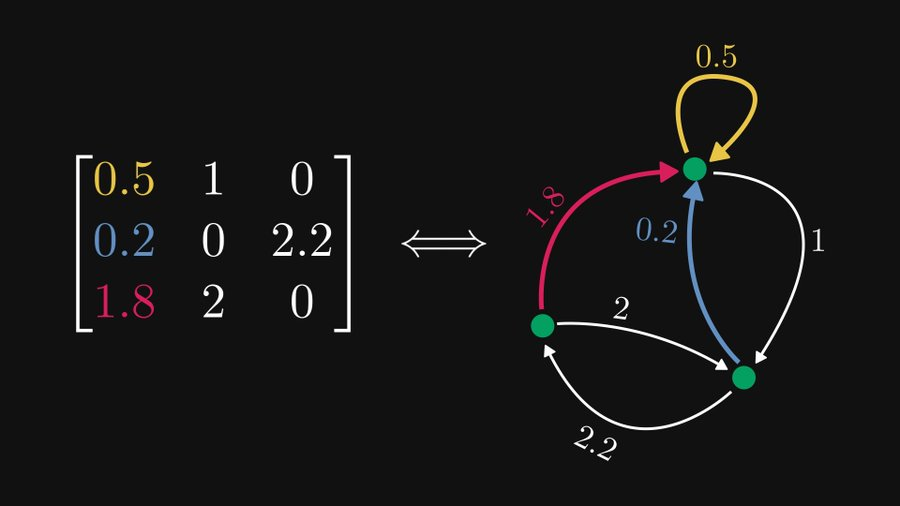
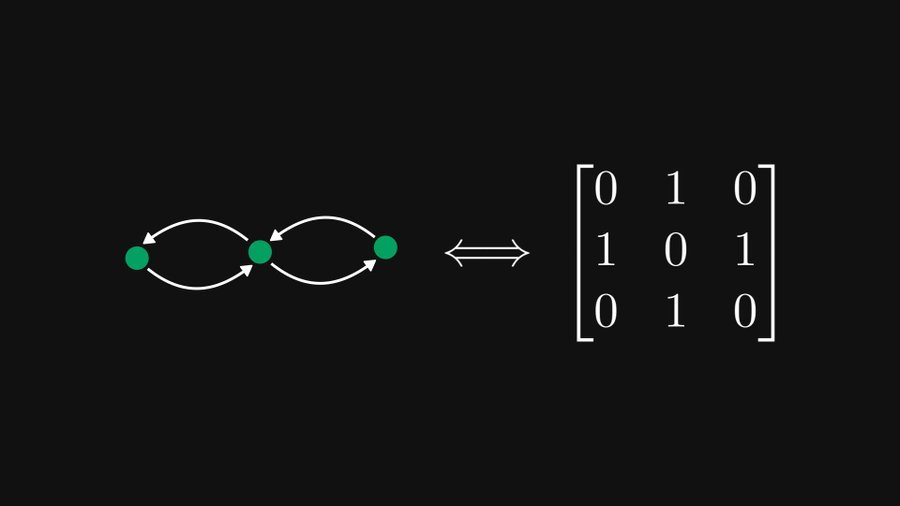
아래 그림과 같이 왼쪽의 3×3 행렬은 실제로 오른쪽의 3개 노드를 포함하는 방향성 그래프와 동일하게 표현될 수 있으며, 이러한 표현은 행렬 이론과 그래프 이론 모두에 매우 유용합니다.

이 예는 모든 사람이 수학에 접근할 수 있도록 최선을 다하는 수학자 Tivadar Danka의 작품입니다. 자칭 "혼돈의 선" 수학자인 그는 일련의 트윗과 블로그 게시물을 통해 행렬과 그래프의 동등성과 그 사용법을 생생하게 소개했습니다. 현재까지 해당 트윗은 200만 번 이상 읽혔고, 3,200개 이상의 리트윗과 9,100개 이상의 즐겨찾기를 받았습니다.

행렬과 방향 그래프의 원자가

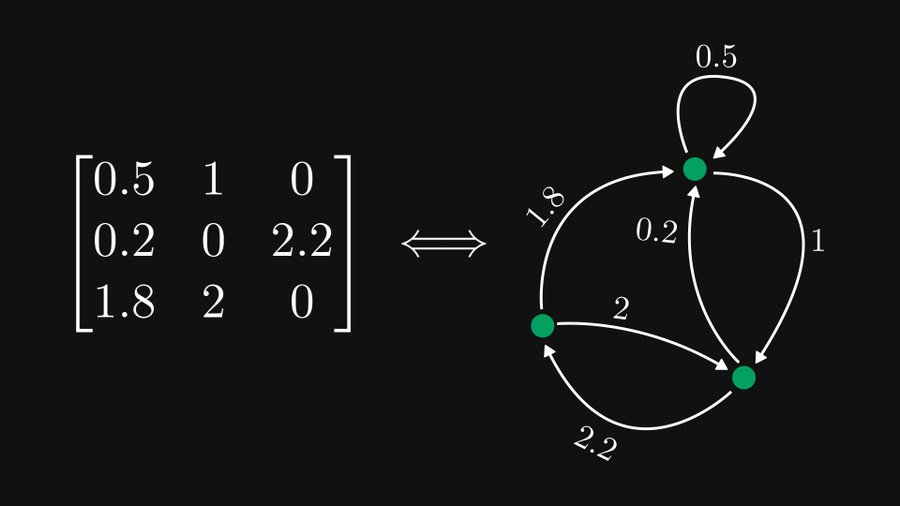
위의 예에서 볼 수 있듯이 각 행을 노드로 처리하면 각 요소는 방향이 있고 가중치가 부여된 모서리로 표현될 수 있습니다. 물론 0개의 요소는 무시될 수 있습니다. 요소가 행 i와 열 j에 있는 경우 노드 i에서 노드 j까지의 가장자리에 해당합니다.

언뜻 보기에는 복잡해 보일 수 있지만 먼저 노드 중 하나를 살펴보겠습니다.

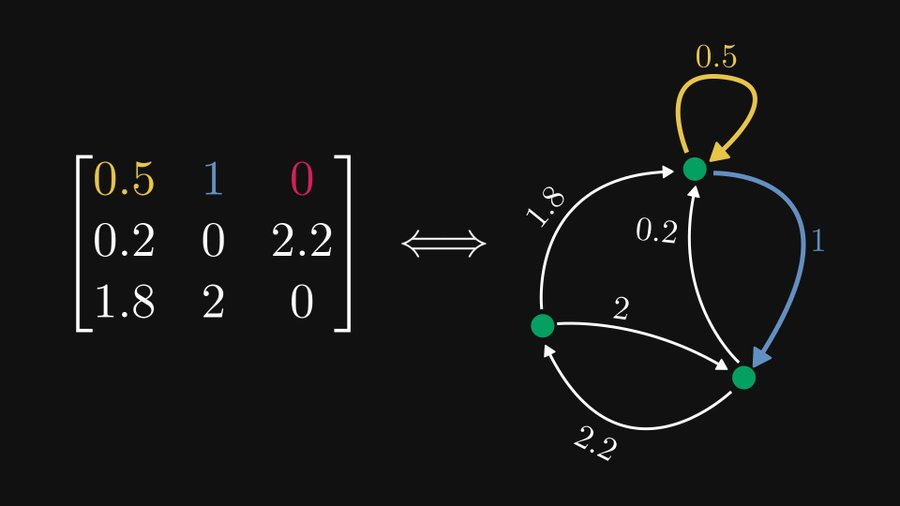
그림에 표시된 대로 이 3×3 행렬의 경우 행 1은 3개의 요소를 포함하지만 그 중 하나가 0인 최상위 노드(여기서는 노드 1이라고 함)에 해당합니다. 따라서 이 노드는 두 개의 요소를 확장합니다. 가장자리. 노란색 가장자리는 (1,1)의 요소 0.5를 나타내므로 가중치가 0.5인 자신을 가리키는 방향이 있는 가장자리입니다. 마찬가지로 파란색 가장자리는 노드 2를 가리키는 가장자리이며 가중치는 1입니다.

이런 식으로 행렬의 i번째 열이 i번째 노드를 가리키는 모든 가장자리에 해당한다는 것을 분석할 수 있습니다.

이 등가 표현의 용도는 무엇인가요?

음수가 아닌 행렬과 유향 그래프 간의 이러한 동등성은 행렬과 그 연산을 더 잘 이해하는 데 도움이 될 뿐만 아니라 일부 계산 프로세스를 단순화하는 데도 도움이 되며 새로운 관점의 이해 다이어그램에서 시작하는 데도 도움이 됩니다.

예를 들어 행렬의 거듭제곱은 그래프의 걷기에 해당합니다.

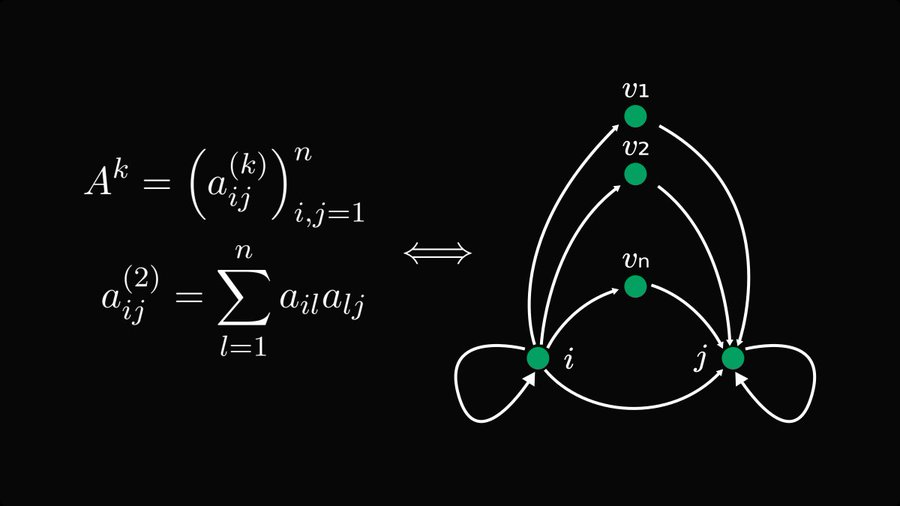
위 그림에 표시된 것처럼 n×n 정사각 행렬 A의 k제곱에 대해 각 요소의 합산 프로세스에는 가능한 모든 k-단계 이동이 포함됩니다.

예를 들어 위의 3×3 행렬의 제곱을 계산한다고 가정해 보겠습니다.

행렬 곱셈을 사용하는 경우 다음과 같이 계산해야 합니다.

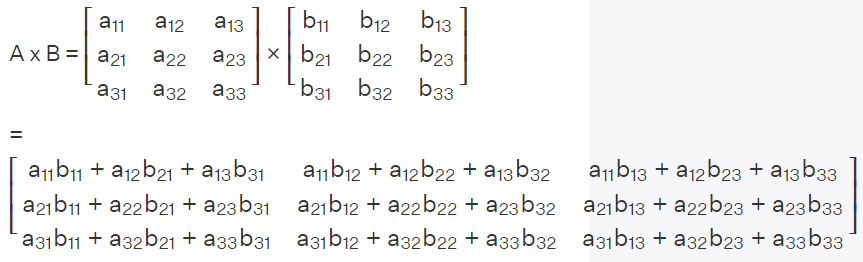
연산 결과의 첫 번째 요소에 대해 결과 = 0.5×0.5+1×0.2+0×1.8을 얻을 수 있습니다. = 0.45. 마지막으로 다음과 같이 완전한 결과를 얻을 수 있습니다.

그러나 위의 그래프 걷기 방법을 사용하면 경로를 걷는 결과를 얻을 수 있습니다. 마찬가지로 결과 행렬의 첫 번째 요소에 대해 a_{1,l}→a_{l,1}을 충족하는 모든 2단계 걷기 경로를 합산해야 합니다.

그러나 이 방향 그래프가 마르코프 체인의 상태를 나타내는 경우 전이 확률 행렬의 제곱은 본질적으로 체인이 2단계 후에 특정 상태에 도달할 확률을 나타냅니다.

그뿐만 아니라, 그래프를 사용하여 행렬을 표현하면 음수가 아닌 행렬의 구조에 대한 심층적인 이해도 얻을 수 있습니다. 이를 위해서는 먼저 "강하게 연결된 구성요소"라는 개념을 이해해야 한다고 Danka는 말했습니다.

강하게 연결된 구성요소

강하게 연결된 구성요소란 무엇인가요? 유향 그래프의 경우 그래프의 다른 모든 노드가 모든 노드에서 도달할 수 있으면 그래프가 강력하게 연결되어 있다고 말합니다. 아래 그림과 같습니다.

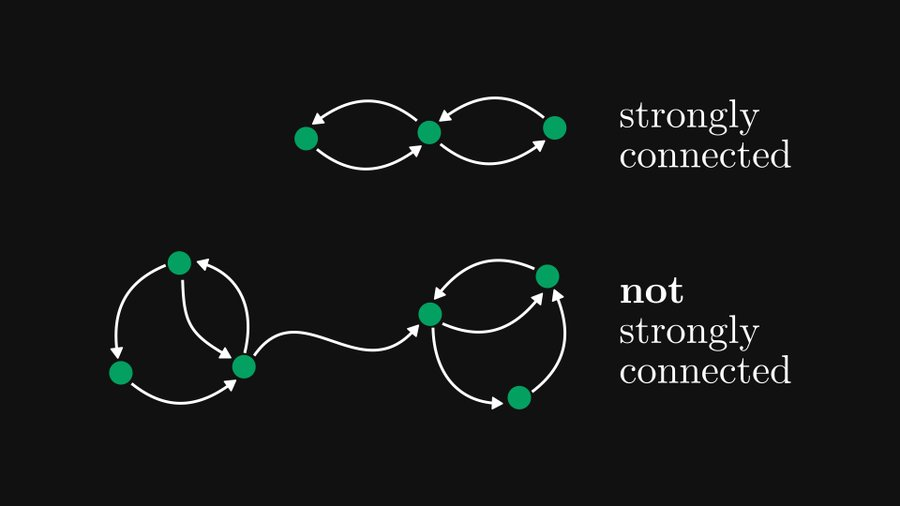
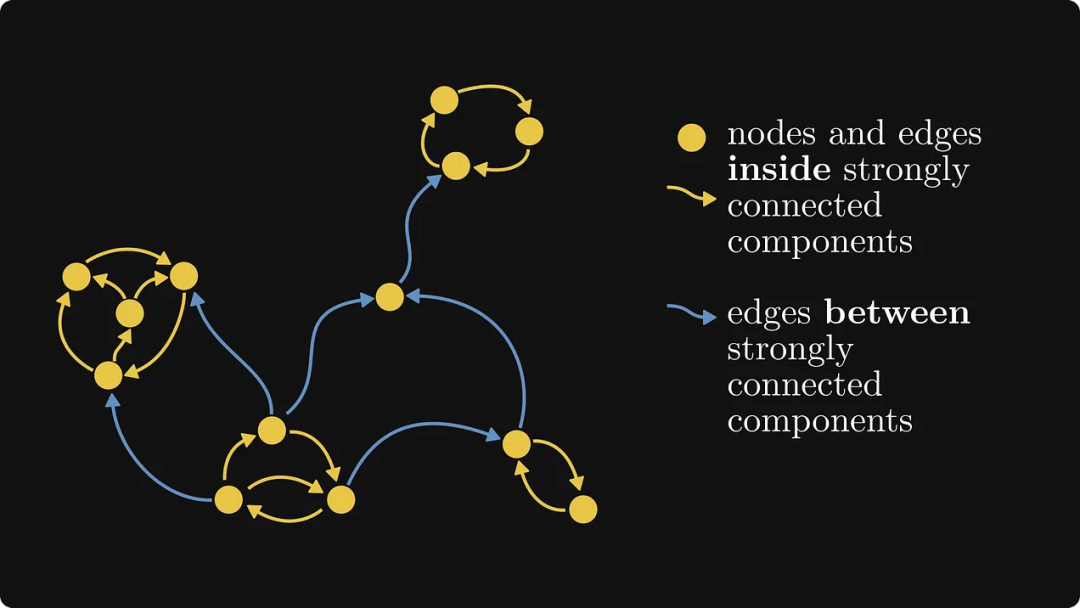
강하게 연결된 구성 요소는 유향 그래프에서 강력한 연결을 달성할 수 있는 부분/하위 그래프를 나타냅니다. 아래 그림과 같이 왼쪽과 오른쪽에는 강하게 연결된 구성 요소가 있고 가운데 흰색 가장자리는 강하게 연결된 구성 요소에 속하지 않습니다.

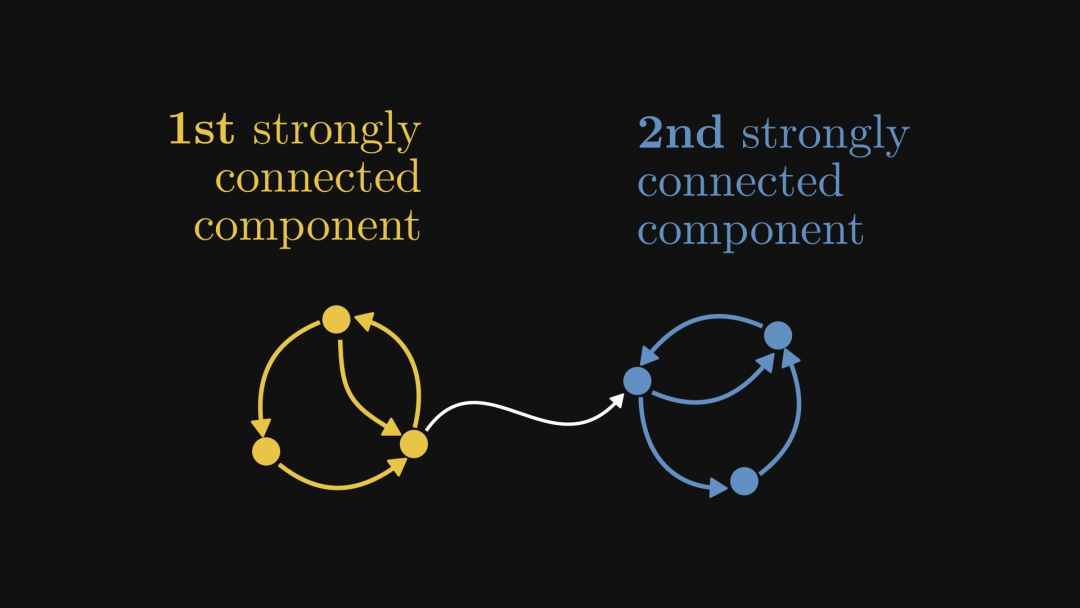
아래 그림은 노란색 부분이 강하게 연결된 구성 요소인 또 다른 예를 보여줍니다.

강하게 연결된 그래프에 해당하는 행렬은 환원 불가능한 행렬인 반면, 음이 아닌 행렬의 다른 모든 행렬은 환원 가능한 행렬이다.

Danka는 예를 들어 설명합니다. (간단함을 위해 예제의 모든 가중치는 단위 가중치이지만 실제로 이러한 가중치 값은 음수가 아닌 모든 값이 될 수 있습니다.)

강하게 연결된 구성 요소를 포함하지만 강하게 연결되지 않은 이 그래프를 옮겨 적겠습니다.

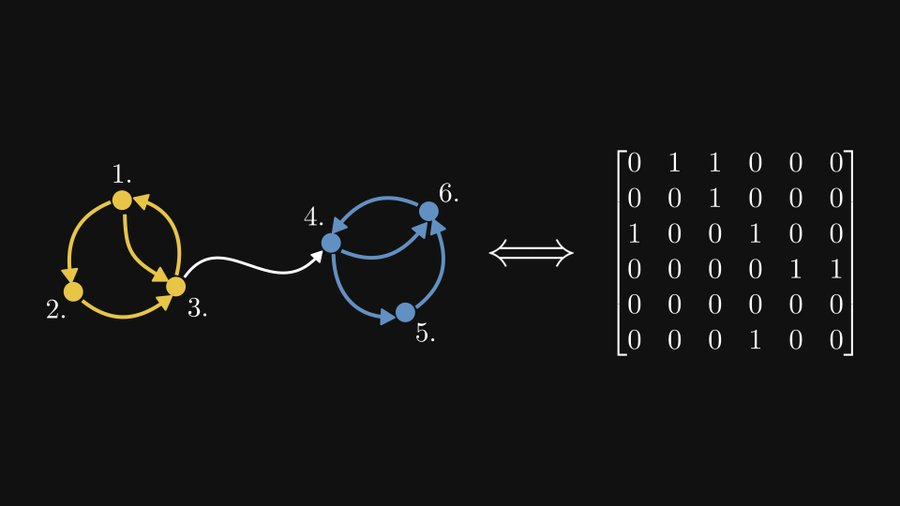
그리고 이 행렬은 환원 가능한 행렬입니다.

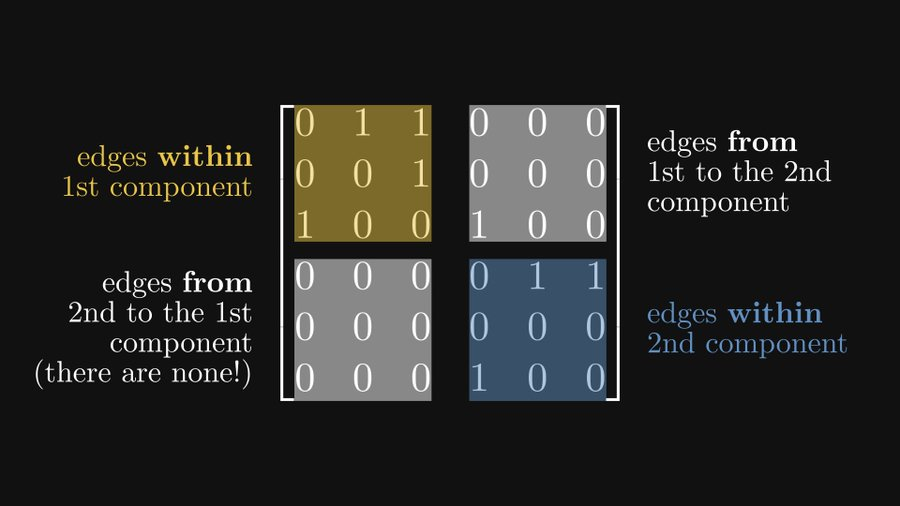
주대각선의 두 하위 행렬은 각각 두 개의 강하게 연결된 구성 요소를 나타내고, 오른쪽 상단의 하위 행렬은 첫 번째 강하게 연결된 구성 요소에서 두 번째로 강하게 연결된 구성 요소까지의 가장자리를 나타냅니다. 왼쪽 아래는 두 번째 강하게 연결된 구성요소에서 첫 번째 강하게 연결된 구성요소까지의 간선을 나타냅니다(그러한 간선이 없기 때문에 모두 0입니다).

이러한 블록 행렬 작성 형식을 Frobenius 정규형이라고 합니다.

그래서 우리는 자연스럽게 질문합니다: 음수가 아닌 행렬을 Frobenius 정규 형식 행렬로 변환할 수 있습니까?

음수가 아닌 행렬을 표현하기 위해 유향 그래프를 사용하면 대답이 '예'라는 것을 쉽게 알 수 있습니다. 음이 아닌 행렬을 표현하는 유향 그래프는 서로 연결된 강력하게 연결된 구성요소로 표현될 수 있기 때문입니다. 이 과정은 매우 간단합니다.

1. 음수가 아닌 행렬에 해당하는 유향 그래프를 구성합니다.

2. 강하게 연결된 구성 요소를 찾습니다.

3. 각 노드에 레이블을 지정하는 더 나은 방법으로 변경합니다.

그렇습니다!

사진을 사용하여 Frobenius 표준 형식을 얻으세요

그렇다면 이보다 더 좋은 방법은 무엇일까요?

위의 예를 바탕으로 과정을 살펴보겠습니다.

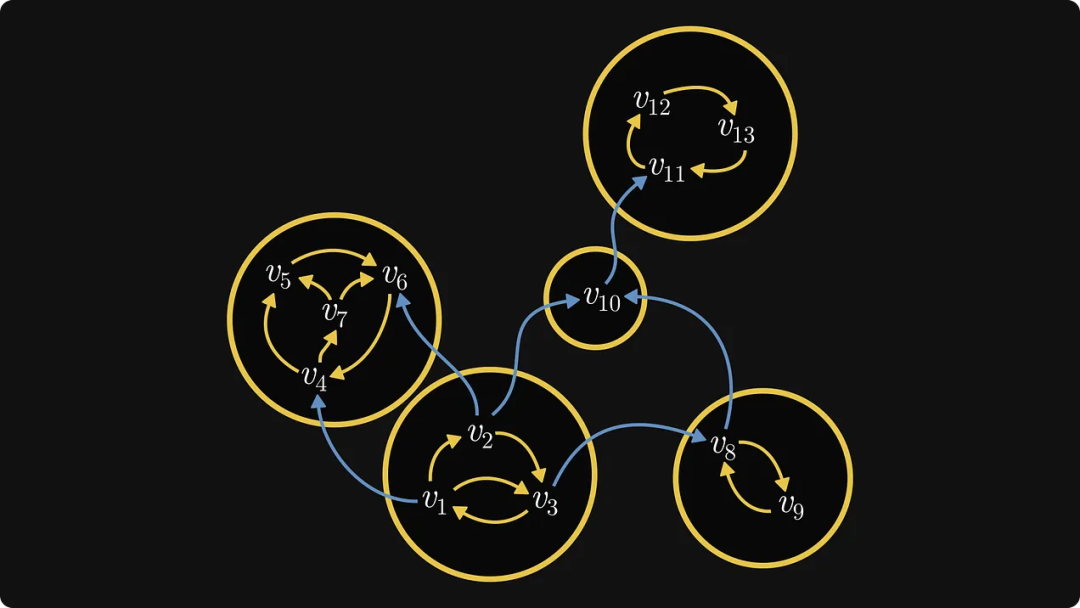
먼저 아래 그림과 같이 강하게 연결된 각 구성 요소를 단일 개체로 융합합니다. 이때 우리는 강력하게 연결된 각 구성요소를 블랙박스로 처리할 수 있습니다. 내부 구조에는 관심이 없고 외부 연결에만 관심이 있습니다.

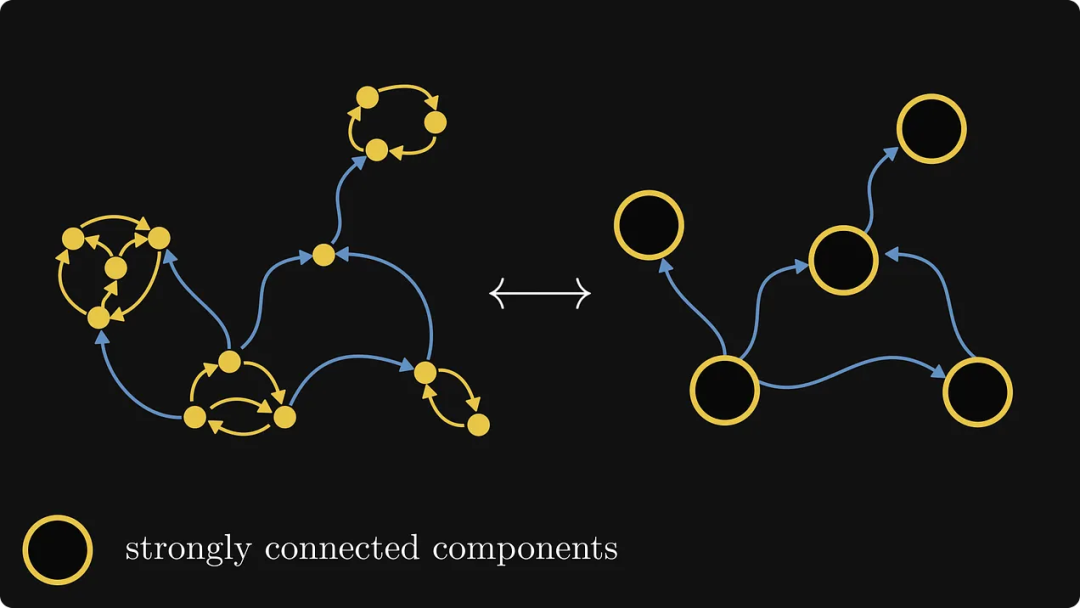
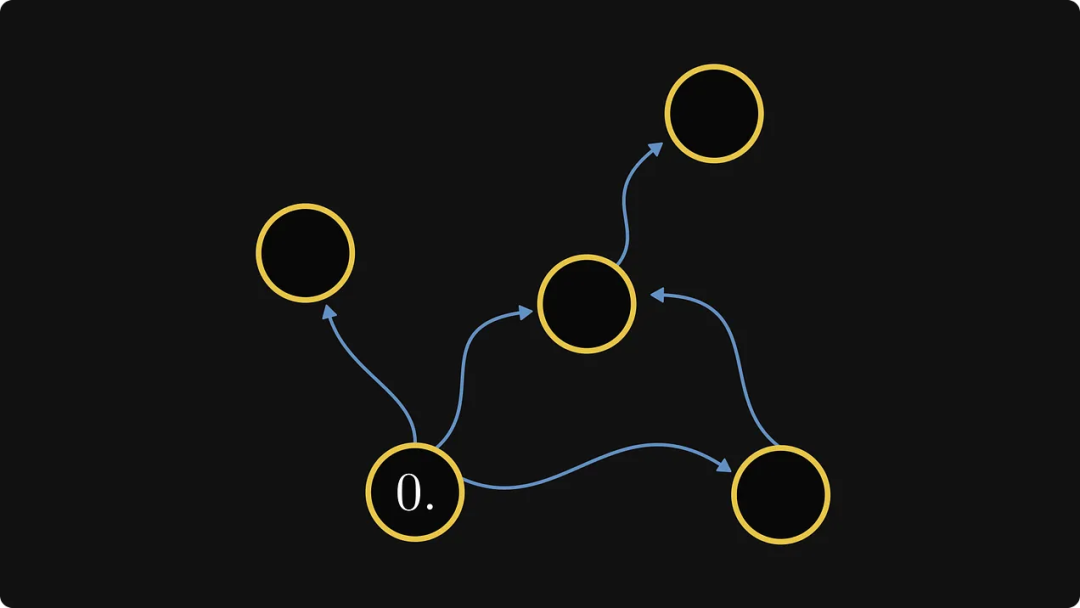
그런 다음 이 새 그래프에서 나가는 가장자리만 있고 들어오는 가장자리가 없는 구성 요소를 찾아야 합니다. 이 특정 예에는 하나만 있으며 번호 0으로 표시합니다.

다음 단계는 더 번거롭습니다. 각 구성 요소의 번호가 숫자 0에서 가장 먼 거리에 있도록 각 구성 요소에 번호를 매깁니다. 다음 예는 이 점을 더 명확하게 설명할 수 있습니다.

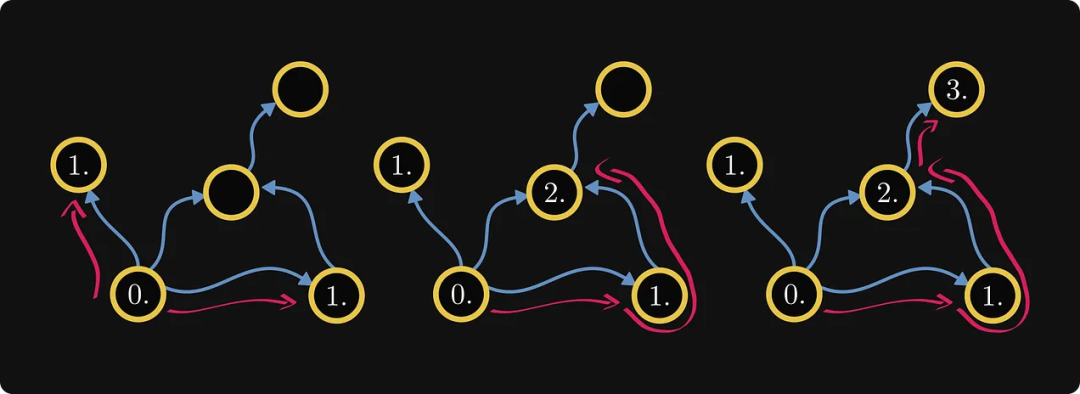
0번부터 중간 구성 요소까지 두 개의 경로가 있음을 볼 수 있으므로 0에서 가장 먼 경로를 선택하여 번호를 매깁니다. 마침내 얻었습니다:

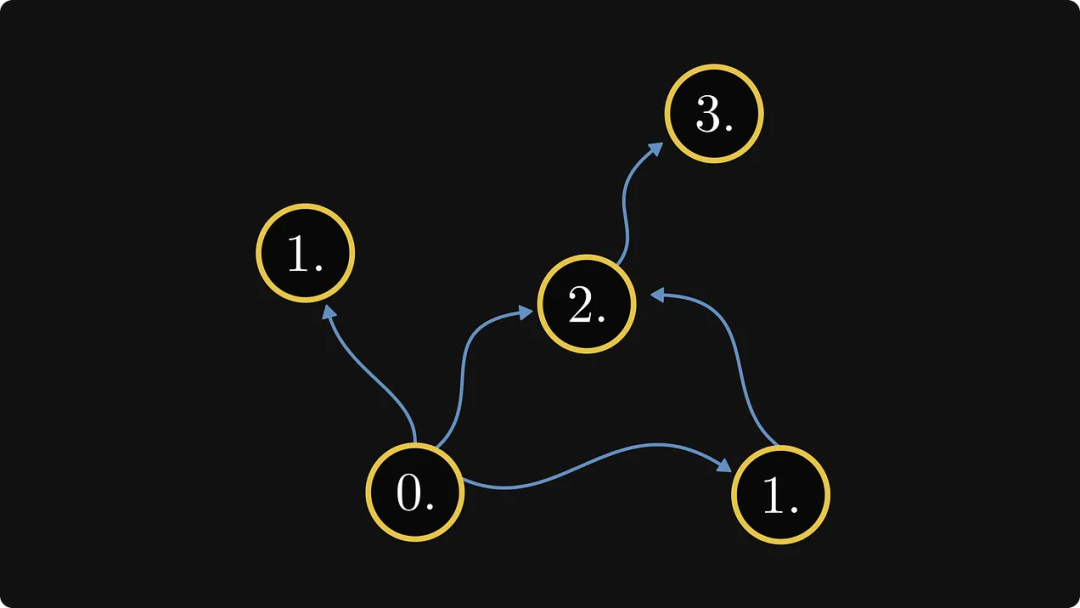
Sebenarnya, ini mentakrifkan susunan komponen. Seterusnya, labelkan nod dalaman setiap komponen:

Jika graf itu sendiri berasal daripada matriks, maka proses pelabelan semula sedemikian boleh menghasilkan matriks kanonik Frobenius!

Sebenarnya, proses pelabelan semula ini adalah menggunakan matriks pilih atur P untuk mengubah matriks asal, dan matriks pilih atur adalah terdiri daripada hasil darab matriks alih berganda.

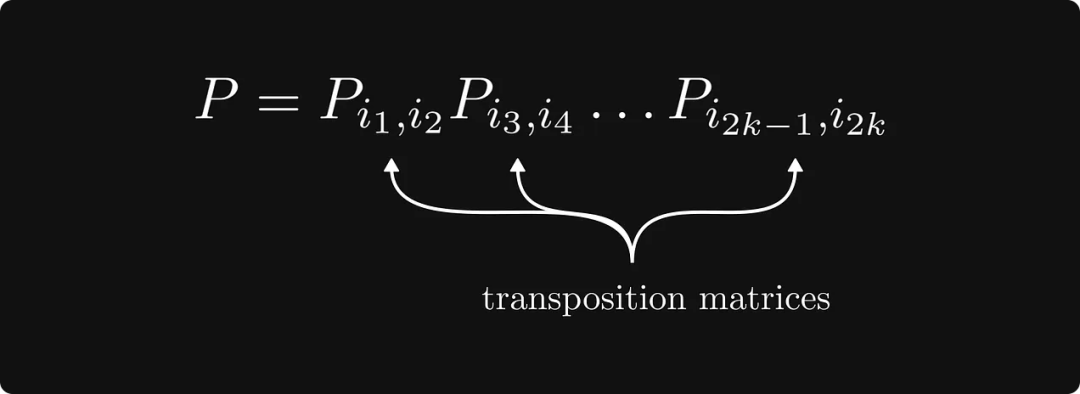
Berikut ialah bentuk lengkap teorem:

Sudah tentu, penggunaan menggunakan graf untuk mewakili matriks melampaui ini Sebagai contoh, kita juga boleh menggunakan nilai eigen matriks untuk menentukan nilai eigen bagi graf. Malah, garis pemikiran ini menimbulkan bidang penyelidikan teori graf spektrum.

Kesimpulan

Jelas sekali, hubungan kesetaraan antara matriks dan graf ini bukan sahaja membantu untuk penyelidikan teori graf, tetapi juga menyediakan perspektif baharu untuk pengiraan dan analisis algebra linear. Ia juga mempunyai beberapa kegunaan praktikal yang penting Contohnya, data DNA sering diwakili dalam bentuk matriks atau graf.

Selain itu, kita semua tahu kepentingan operasi matriks untuk AI model besar semasa, dan graf yang diwakili oleh graf pengetahuan juga menjadi pemacu penting AI semasa melalui teknologi seperti carian yang dipertingkatkan semula. Menghubungkan kedua-duanya mungkin membawa beberapa penemuan baharu dalam kebolehtafsiran AI dan kecerdasan buatan graf. Sekurang-kurangnya, ini membantu kami mempelajari algebra linear dengan lebih baik.

Malah, kandungan di atas diekstrak daripada buku "Mathematics of Machine Learning" yang ditulis oleh Tivadar Danka. Buku ini akan memperkenalkan pengetahuan matematik yang berkaitan dengan pembelajaran mesin daripada tahap yang mudah kepada yang mendalam, membolehkan pembaca benar-benar memahami perkara yang berlaku dan sebabnya Danka dengan yakin mengisytiharkan bahawa ini akan menjadi "sumber terbaik untuk pembelajaran mesin." Pada masa ini, beliau telah mengeluarkan dua pratonton bab dalam talian. Pembaca yang berminat boleh layari: https://tivadardanka.com/mathematics-of-machine-learning-preview/

.

위 내용은 선 생성을 배울 때 왜 행렬과 그래프 사이에 등가 관계가 있는지 몰랐나요?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!