비용이 포함된 최대 포인트 수
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB원래의
- 2024-08-18 06:46:021071검색
1937. 비용 대비 최대 포인트
난이도:중
주제: 배열, 동적 프로그래밍
m x n 정수 행렬 포인트(0-인덱스)가 제공됩니다. 0점부터 시작하여 행렬에서 얻을 수 있는 점수를 최대화하고 싶습니다.
포인트를 얻으려면 각 행에서 하나의 셀을 선택해야 합니다. 좌표(r, c)에서 셀을 선택하면 점수에 추가점[r][c]이 됩니다.
그러나 이전 행에서 선택한 셀에서 너무 멀리 있는 셀을 선택하면 점수를 잃게 됩니다. 인접한 두 행 r 및 r + 1(여기서 0 1) 및 (r + 1, c에서 셀을 선택합니다. 2)은 점수에서 abs(c1 - c2)를 뺍니다.
달성할 수 있는 최대포인트를 반환합니다.
abs(x)는 다음과 같이 정의됩니다.
-
x >= 0.
- -x는 x < 0.
예 1:
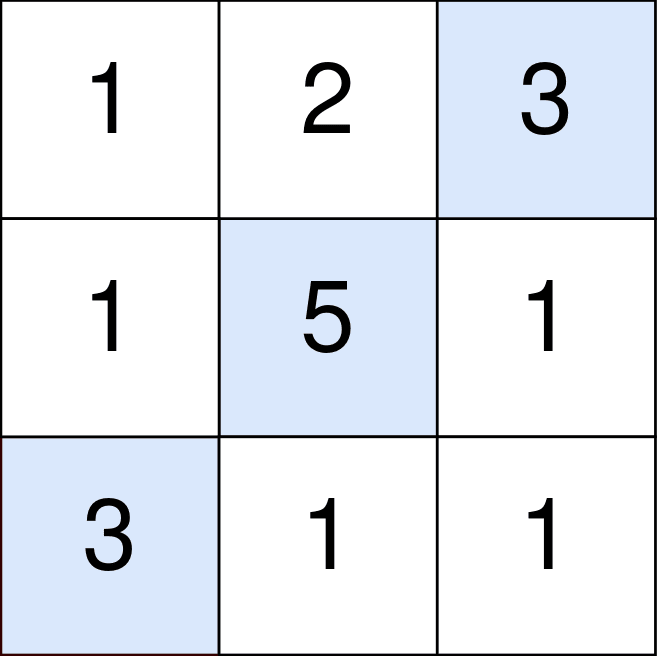
- 입력: l1 = [2,4,3], l2 = [5,6,4]
- 출력: 9
- 설명:
- 파란색 셀은 선택할 최적의 셀을 나타내며 좌표가 (0, 2), (1, 1), (2, 0)입니다.
- 점수에 3 + 5 + 3 = 11을 더합니다.
- 단, 점수에서 절대(2 - 1) + 절대(1 - 0) = 2를 빼야 합니다.
- 최종 점수는 11 - 2 = 9입니다.
예 2:
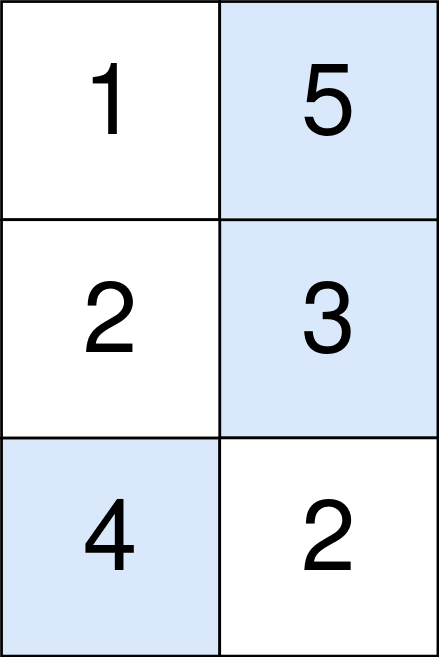
- 입력: 포인트 = [[1,5],[2,3],[4,2]]
- 출력: 11
- 설명:
- 파란색 셀은 선택할 최적의 셀을 나타내며 좌표가 (0, 1), (1, 1), (2, 0)입니다.
- 점수에 5 + 3 + 4 = 12를 더합니다.
- 단, 점수에서 절대(1 - 1) + 절대(1 - 0) = 1을 빼야 합니다.
- 최종 점수는 12 - 1 = 11입니다.
제약조건:
- m == 포인트.길이
- n == 포인트[r].길이
- 1 <= m, n <= 10
- 5 1 <= m * n <= 10
- 5 0 <= 포인트[r][c] <= 10
- 5
힌트:
- 동적 프로그래밍을 사용해 보세요.
- dp[i][j]는 points[i][j]가 선택한 가장 최근 셀인 경우 얻을 수 있는 최대 포인트 수입니다.
해결책:
해결책을 여러 단계로 나눌 수 있습니다.1단계: DP 배열 정의
2D 배열 dp를 사용합니다. 여기서 dp[i][j]는 i행과 j열의 셀을 선택하여 얻을 수 있는 최대 포인트를 나타냅니다.
2단계: DP 어레이 초기화
비용을 뺄 이전 행이 없으므로 dp의 첫 번째 행을 포인트의 첫 번째 행과 동일하게 초기화합니다.
3단계: 각 행의 DP 값 계산
각 후속 행에 대해 이전 행에서 전환하는 데 드는 비용을 고려하여 각 열에 가능한 최대 포인트를 계산합니다.
i-1행에서 i행으로의 전환을 효율적으로 계산하기 위해 왼쪽과 오른쪽에 두 개의 보조 배열을 사용할 수 있습니다.
-
left[j]는 왼쪽으로부터의 전환만을 고려하여 j번째 열에 대해 달성할 수 있는 최대값을 저장합니다.
- right[j]는 오른쪽으로부터의 전환만 고려하여 j번째 열에 대해 달성할 수 있는 최대값을 저장합니다.
i행의 각 열 j에 대해:
- 왼쪽[j] 또는 오른쪽[j]에 포인트[i][j]를 더한 최대값을 사용하여 dp[i][j]를 업데이트합니다.
결과는 dp 배열의 마지막 행에 있는 최대값이 됩니다.
이 솔루션을 PHP로 구현해 보겠습니다:
1937. 비용 대비 최대 포인트
설명:
- 왼쪽 및 오른쪽 배열: 이전 행의 값을 고려하여 각 셀에 대해 얻을 수 있는 최대 점수를 계산하고 열 간 이동으로 인한 페널티를 효율적으로 계산하는 데 도움이 됩니다.
- 동적 프로그래밍 접근 방식: 이 방법을 사용하면 각 행이 이전 행을 기반으로 계산되므로 대규모 행렬에 맞게 솔루션을 확장할 수 있습니다.
연락처 링크
이 시리즈가 도움이 되었다면 GitHub에서 저장소에 별표를 표시하거나 즐겨찾는 소셜 네트워크에서 게시물을 공유해 보세요. 여러분의 지원은 저에게 큰 의미가 될 것입니다!
이렇게 더 유용한 콘텐츠를 원하시면 저를 팔로우해주세요.
- 링크드인
- 깃허브
위 내용은 비용이 포함된 최대 포인트 수의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
php Integer Array define if for try break using Length number this transition column input th github
성명:
본 글의 내용은 네티즌들의 자발적인 기여로 작성되었으며, 저작권은 원저작자에게 있습니다. 본 사이트는 이에 상응하는 법적 책임을 지지 않습니다. 표절이나 침해가 의심되는 콘텐츠를 발견한 경우 admin@php.cn으로 문의하세요.

