수십 년 만에 처음으로 진전이 이루어졌으며 견습생 Tao Zhexuan과 Zhao Yufei가 조합 수학 문제를 돌파했습니다.
- WBOY원래의
- 2024-08-15 17:04:21320검색
Récemment, pour la première fois, des progrès ont été réalisés sur un problème mathématique non résolu vieux de plusieurs décennies.
Les moteurs de ces progrès sont James Leng, étudiant diplômé de l'UCLA, Ashwin Sah, étudiant diplômé en mathématiques du MIT, et Mehtaab Sawhney, professeur adjoint à l'Université de Columbia. Parmi eux, James Leng a étudié auprès du célèbre mathématicien Terence Tao et Ashwin Sah a étudié auprès du maître de mathématiques discret Zhao Yufei.
Adresse papier : https://arxiv.org/pdf/2402.17995
Pour comprendre l'avancée réalisée dans cette recherche, il faut commencer par les progressions arithmétiques.
La somme des n premiers termes d'une suite arithmétique est appelée une série arithmétique, également appelée série arithmétique. En 1936, les mathématiciens Paul Erdős et Pál Turán ont émis l'hypothèse que si un ensemble est constitué de fractions non nulles d'entiers (même 0,00000001 %), alors il doit contenir une série arithmétique arbitrairement longue. Les seuls ensembles qui peuvent éviter les séries arithmétiques sont ceux qui contiennent une partie « négligeable » des entiers. Par exemple, l'ensemble {2, 4, 8, 16,…}, où chaque nombre est le double du nombre précédent, s'étale le long de l'axe des nombres sans progression.
En 1975, le mathématicien Endre Szemerédi a prouvé cette conjecture. Ses travaux ont donné naissance à diverses directions de recherche que les mathématiciens explorent encore aujourd’hui.
Les mathématiciens ont établi le résultat de Szemerédi dans le contexte d'un ensemble fini de nombres (tous les nombres entiers de 1 à un nombre N). Quelle part de la réserve initiale peut être utilisée dans l’extension avant d’inclure inévitablement une série interdite ? Comment cette proportion change-t-elle lorsque N change ?
Par exemple, que N soit 20, combien de ces 20 nombres peuvent être écrits tout en évitant les séries de 5 nombres ou plus ? Il s’avère que la réponse est de 16 à 80 % du pool initial.
Szemerédi a été le premier à montrer que lorsque N grandit, cette fraction doit diminuer jusqu'à zéro, et les mathématiciens ont depuis tenté de quantifier la rapidité avec laquelle cela se produit.
L'année dernière, des travaux révolutionnaires menés par deux informaticiens ont presque résolu le problème des séries à trois termes, telles que {6, 11, 16}. Mais le problème devient plus difficile lorsque l’on essaie d’éviter les séries arithmétiques de quatre termes ou plus. En effet, les séries plus longues reflètent des structures sous-jacentes difficiles à révéler à l’aide des méthodes mathématiques classiques.
Les nombres x, y et z dans la série arithmétique à trois termes satisfont toujours à l'équation simple x – 2y + z = 0 (en prenant la série {10, 20, 30} comme exemple : 10 – 2*(20) + 30 = 0), il est relativement facile de prouver si un ensemble contient des nombres qui satisfont à cette condition. Alors que les nombres d'une série de quatre termes doivent également satisfaire l'équation plus complexe x^2 – 3y^2 + 3z^2 – w^2 = 0, une série de cinq termes ou plus doit satisfaire une équation encore plus complexe. Cela signifie que les ensembles contenant de telles séries présenteront des motifs plus subtils. Il serait également plus difficile pour les mathématiciens de prouver qu’un tel modèle existe.
À la fin des années 1990, le mathématicien Timothy Gowers a proposé une théorie pour surmonter cet obstacle. Il a ensuite reçu la médaille Fields, la plus haute distinction mathématique, en partie pour ce travail. En 2001, il a appliqué sa méthode au théorème de Szemerédi, prouvant de meilleures limites sur la taille maximale de l'ensemble, évitant ainsi les séries arithmétiques pour une longueur donnée.
En 2022, James Leng, alors étudiant de deuxième année à l'UCLA, a commencé à comprendre la théorie de Gowers. Il n'a pas considéré le théorème de Szemerédi. Il espère plutôt répondre aux questions sur l'approche de Gowers.
Cependant, après avoir essayé d'explorer pendant plus d'un an, il n'a rien trouvé.
Sah et Sawhney, qui ont réfléchi à des questions connexes, ont découvert le travail de Leng et ont été très intéressés. Sawhney a même déclaré : « Je suis surpris de pouvoir penser ainsi.
Sah et Sawhney ont réalisé que les recherches de Leng pourraient les aider à progresser davantage sur le théorème de Szemerédi. En quelques mois, trois jeunes mathématiciens ont découvert comment obtenir de meilleures limites supérieures pour la taille des ensembles sans séries penttermes. Ils ont ensuite étendu leurs travaux à des séries de longueurs arbitraires, marquant le premier progrès sur le problème au cours des 23 années écoulées depuis la preuve de Gowers.
Soit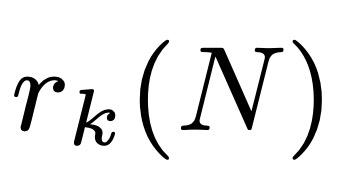 
désignant 
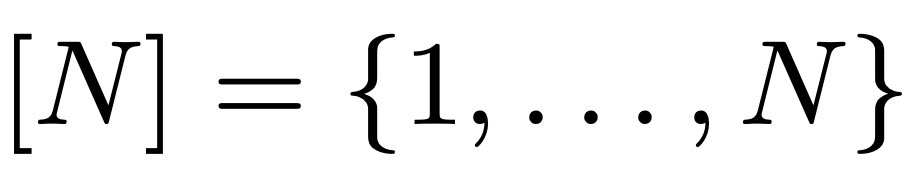, la taille du plus grand sous-ensemble d'une série arithmétique sans k termes. Leng, Sah et Sawhney ont montré que pour k ≥ 5, il existe c_k > 0 tel que 
.
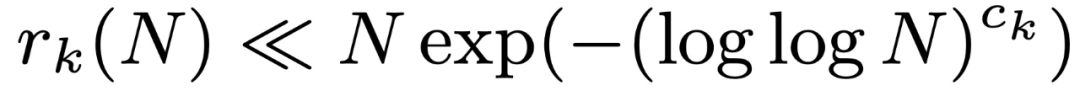Équipe de recherche
Le premier auteur de l'article, James Leng, est un étudiant diplômé en mathématiques à l'Université de Californie à Los Angeles (UCLA) et a obtenu son diplôme de premier cycle à l'Université de Californie à Berkeley. Il a étudié auprès du célèbre mathématicien Terence Tao.
James Leng의 연구 관심분야는 산술 조합론, 동적 시스템, 푸리에 분석 등입니다. 그의 연구는 NSF 대학원 펠로우십의 지원을 받았습니다. ㅋㅋ 2016년 여름, 16세의 Sah는 국제 수학 올림피아드(IMO)에서 금메달을 획득했습니다. 이듬해 그는 공부하기 위해 MIT에 입학했습니다. ㅋㅋ Ashwin Sah
두 번째는 Mehtaab Sawhney인데, 수업시간에 만나 친구가 되었습니다. 나중에 두 사람은 함께 연구하고 그래프 이론, 확률 이론, 랜덤 행렬의 속성과 같은 이산 수학 분야의 다양한 주제에 대해 논의했습니다. Ashwin Sah와 Mehtaab Sawhney는 (MIT) 학부생이었던 2017년 말에 만났습니다. 그 이후로 두 사람은 57개의 놀라운 수학적 증명을 함께 작성했으며 그 중 다수는 다양한 분야에서 심오한 결과를 가져왔습니다.
Mehtaab Sawhney
Mehtaab Sawhney는 현재 Columbia University의 조교수입니다. 그의 연구 관심 분야로는 조합론, 확률, 이론 컴퓨터 과학 등이 있습니다.
참조 링크: https://www.Quantamagazine.org/grad-students-find-inevitable-patterns-in-big-sets-of-numbers-20240805/위 내용은 수십 년 만에 처음으로 진전이 이루어졌으며 견습생 Tao Zhexuan과 Zhao Yufei가 조합 수학 문제를 돌파했습니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!