리만 가설의 중요한 돌파구! 타오저쉬안(Tao Zhexuan)은 MIT와 옥스퍼드의 새로운 논문을 적극 추천했으며, 37세의 필즈상 수상자도 참여했다.

최근 밀레니엄 7대 문제 중 하나로 알려진 리만 가설이 새로운 돌파구를 맞이했습니다.

리만 가설은 소수 분포의 정확한 특성과 관련된 수학에서 매우 중요한 미해결 문제입니다(소수는 1과 자기 자신으로만 나눌 수 있는 숫자이며, 수학에서 근본적인 역할을 합니다). 정수론 역할).

오늘날의 수학 문헌에는 리만 가설(또는 일반화된 형식)의 확립에 기초한 수천 가지 이상의 수학적 명제가 있습니다. 즉, 리만 가설과 그 일반화된 형식이 입증되면 천 개가 넘는 명제가 정리로 확립되어 수학 분야에 지대한 영향을 미칠 것이며, 리만 가설이 틀린 것으로 입증된다면, 이러한 제안의 일부도 그 효과를 잃을 것입니다.

새로운 돌파구는 MIT 수학 교수 Larry Guth와 옥스퍼드 대학교 수학 연구소 교수이자 필즈상 수상자 James Maynard의 논문에서 나왔습니다. 이 논문을 추천한 수학자 테렌스 타오(Terence Tao)는 리만 제타 함수의 영점에 바인딩된 고전적인 1940년 Ingham에 대한 최초의 실질적인 개선을 제공했다고 말했습니다(더 일반적으로는 다양한 Dirichlet 계열의 큰 값을 제어하는 ​​데 있어서). 이전에는 80여년 전에 탄생한 잉햄 경계(Ingham Bound)는 개선이 부족하여 수학자들이 해석적 정수론에서 많은 일을 하는 것을 제한했습니다.

그러나 도저쉬안(Tao Zhexuan)은 이것이 비록 중요한 돌파구이기는 하지만 리만 가설을 완전히 해결하려면 아직 멀었기 때문에 합리적으로 보아야 한다고 말했습니다.

리만 가설이란 무엇인가요?

리만 가설 또는 리만 가설은 1859년 독일 수학자 베른하르트 리만이 제안했습니다. 이 추측은 소수의 분포와 밀접하게 관련되어 있으며 그 핵심 내용은 리만 제타 함수의 중요한 0과 관련되어 있습니다. ㅋㅋㅋ                                                                                                  베른하르트 리만, 출처:facts.net/

리만 가설의 내용은 완전히 초등수학으로는 설명할 수 없습니다. 대략적으로 말하면 리만 제타 함수(즉, 변수와 함수 값이 모두 복소 영역에서 값을 가질 수 있는 함수)라는 복소 변수 함수에 대한 추측이다. 다른 많은 함수와 마찬가지로 리만 제타 함수는 특정 지점에서 0 값을 갖습니다. 이러한 점을 리만 제타 함수의 영점이라고 합니다. 이러한 0 중에는 리만 제타 함수(Riemann zeta function)라고 불리는 특히 중요한 중요하지 않은 0이 있습니다. 리만 가설이 예측하는 것은 모든 중요하지 않은 영점이 "임계선"이라고 불리는 특별한 직선에 분포되어 있다는 것입니다(대중 과학 작가 Lu Changhai의 블로그에서 인용).

리만 ζ 함수는 다음과 같이 정의됩니다.

리만 가설은 ζ 함수의 모든 중요하지 않은 0의 실수 부분이 1/2이라는 것입니다. 이는 ζ(s)=0이고 s가 중요한 0인 경우(즉, s가 음수가 아닌 경우) s의 실수 부분은 1/2이어야 함을 의미합니다.

리만 가설은 오늘날 세계에서 가장 중요하고 가장 기대되는 수학 문제입니다. 이 추측이 사실이라면 자연수 사이의 소수 분포를 정확하게 기술할 수 있으며, 이는 정수론, 복소해석 및 기타 수학 분야를 해결하는 데 폭넓게 적용되고 영향을 미칠 것입니다.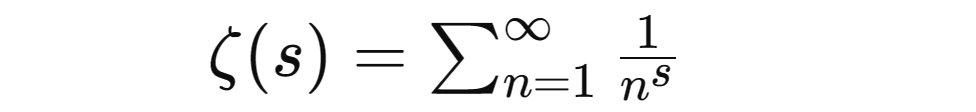

리만 가설이 제안된 지 165년이 지났습니다. 리만 가설을 증명하려는 많은 연구가 있었지만 모두 실패했습니다.

리만 가설을 풀기 위한 시도

리만 가설이 제안된 이후 많은 수학자들이 그 증거를 탐구하는 여정을 시작했습니다.

1896년 프랑스 수학자 Jacques Adamard와 Charles Jean de la Vallée-Poussin은 직선 위에 영점이 없다는 것을 독립적으로 증명했습니다. 리만이 중요하지 않은 0에 대해 증명한 다른 속성과 함께 이는 모든 중요하지 않은 0이 영역에 있어야 함을 보여줍니다. 이는 소수 정리의 첫 번째 완전한 증명에서 중요한 단계입니다. 1900년 독일 수학자이자 현대 수학의 아버지 중 한 명인 다비드 힐베르트는 그의 유명한 23개 질문에 리만 가설을 포함시켰고, 골드바흐의 가설과 함께 힐베르트 목록 질문 8번을 구성했습니다. 동시에 리만 가설은 클레이 수학 연구소의 밀레니엄상에 포함된 유일한 힐베르트 문제이기도 합니다.

1914년 영국의 수학자 고드프리 해롤드 하디는 직선 위에 무한한 영점이 있다는 것을 증명했습니다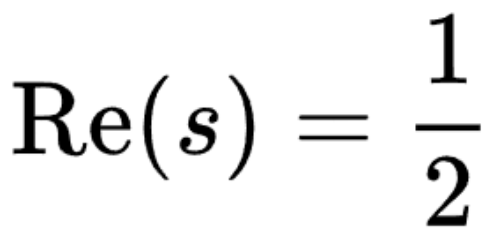. 나중에 Hardy와 영국 수학자 John Unther Littlewood는 1921년, Selberg는 1942년에 임계선 정리(임계선 정리)를 통해 임계선에서 영점의 평균 밀도를 계산했습니다.

최근 몇 년까지 리만 가설을 증명하려는 시도는 종종 논란을 불러일으켰습니다.

2018년 9월, 하이델베르그에서 열린 전례 없는 연설이 수학계를 뒤흔들었습니다. 89세의 아티야 경의 리만 가설 증명이 전 세계의 주목을 받았습니다. 스포트라이트를 받으며 아티야 경은 150년 이상의 역사를 지닌 이 수학적 추측의 증거를 세상에 발표하는 데 45분을 소비했습니다.

하지만 아티야 경의 증거는 PPT의 다음 페이지에 불과합니다. 그러한 증거는 설득력이 없어 보입니다. 리만 가설을 풀었는지 묻는 질문에 그는 "그것은 당신의 논리에 달려 있다. 당신이 모순에 의한 증명을 받아들이지 않는 수학자 아닌 이상 나는 원래의 리만 가설을 증명했다"고 답했다. 모든 문제를 해결한 것은 아니며 앞으로도 많은 문제가 있을 것입니다. 그는 단지 첫 번째 단계를 밟았을 뿐입니다(첫 번째 단계가 해결책입니다).

슬프게도 Atiyah 경은 2019년 1월에 세상을 떠났습니다.

이제 누군가가 리만 가설에 도전했습니다.

Guth와 Maynard가 한 일

Guth와 Maynard의 새로운 돌파구에 대해 유명한 수학자 Teresa Tao는 다음과 같이 말했습니다. "Guth와 Maynard는 Riemann 가설을 연구하는 데 중요한 진전을 이루었습니다. -수학 문제는 아직 갈 길이 멀다."

논문 링크: https://arxiv.org/pdf/2405.20552

우리는 Tao Zhexuan의 트윗을 통해 이 연구가 처음이라는 것을 알게 되었습니다. 수학자 Albert Ingham은 1940년경에 리만 제타 함수의 영점(더 일반적으로는 다양한 디리클레 급수를 지배하는 큰 값)의 고전적 한계에서 상당한 개선이 이루어졌습니다.

1940년 수학자 Albert Ingham은 이러한 영점을 설명하는 경계를 제안했는데, 이는 당시 이론 연구의 기초가 되었습니다. 그러나 Guth와 Maynard의 연구 이전에는 이 경계가 거의 다듬어지지 않았습니다. Guth와 Maynard의 연구는 Ingham의 이러한 경계를 개선했을 뿐만 아니라 그들의 방법은 많은 정수론과 분석 문제에서 중요한 Dirichlet 급수의 큰 값을 처리하기 위한 새로운 도구와 관점을 제공했습니다.

이 논문은 디리클레 다항식의 큰 값의 빈도에 대한 새로운 한계를 증명합니다. 이는 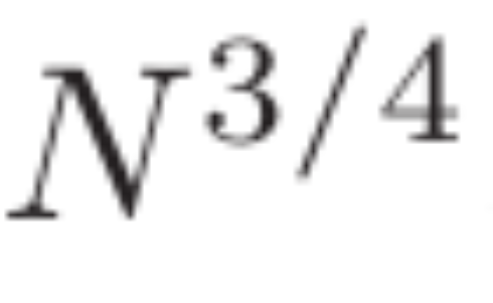에 가까운 값을 갖는 길이 N의 Dirichlet 다항식에 대한 향상된 추정치를 제공합니다. 또한, 이 연구는 영점 밀도 추정치 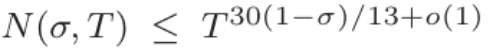와 짧은 길이 간격의 소수에 대한 점근 표현 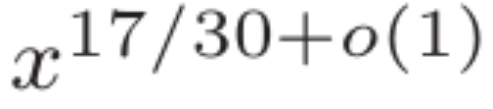을 도출합니다.

Tao Zhexuan 자신이 이 연구에 대해 수학적 관점에서 몇 가지 설명을 했습니다. ?(σ,?)는 실수 부분이 최소 σ이고 허수 부분이 최대 T인 리만 ζ 함수의 0 개수를 나타냅니다. 리만 가설은 N(σ,?)이 σ > 1/2인 경우 사라질 것이라고 말하지만 이 가설은 아직 입증될 수 없습니다. 그러나 차선책으로 수학자들은 ?(σ,?) 의 중요한 상한인 영점 밀도 추정치를 증명할 수 있습니다.

σ=3/4가 핵심값인 것으로 밝혀졌습니다. 1940년에 Ingham은 경계 ?(3/4,?)``?(3/5+?(1))을 도출했습니다.

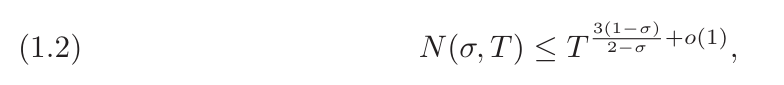
향후 80년 동안 이 경계에 대한 개선은 ?(1) 오류의 사소한 개선에 불과했습니다. 이로 인해 연구자들은 해석적 수 이론에서 더 심층적인 연구를 수행할 수 없게 됩니다. 예를 들어 (?,?+?^?) 형식의 거의 모든 짧은 간격에서 좋은 소수 정리를 얻기 위해 사람들은 오랫동안 제한되어 왔습니다. ?>1/6 범위로 변경하는 경우 주요 장애물은 Ingham 경계에 대한 개선이 부족하다는 것입니다.

Guth와 Maynard는 마침내 Ingham 경계를 3/5=0.6에서 13/25=0.52로 개선했습니다. 예를 들어, 연구자들은 이제 θ>1/6=0.166…에서 θ>2/15=0.133…까지 거의 모든 짧은 간격으로 소수 정리의 범위를 증명할 수 있습니다.

저자 소개

Larry Guth는 2019년 7월부터 MIT에서 Claude E. Shannon 수학 교수로 재직했으며 2021년에 MacVicar Fellow로 선출되었습니다.

그는 Tom Mrowka의 지도하에 2005년 MIT에서 박사 학위를 받았습니다. 그 후 스탠포드 대학에서 박사후 연구원, 토론토 대학의 주니어 교수직을 거쳐 2011년에 그는 Courant Institute 교수로 임명되었습니다. 이후 2012년 MIT 수학과 교수로 부임했다.

Guth의 연구 관심분야는 미터기하학, 조화해석, 극값 조합입니다. 미터법 기하학은 길이, 면적 및 부피와 관련된 불평등에 대한 연구를 의미합니다. 일부 주요 예로는 등각 불평등 및 수축 불평등이 있습니다. 수축 부등식은 Guth 작업의 초점이었으며 또 다른 초점은 기하학적 부등식과 위상수학 사이의 연결을 찾는 것이었습니다.

최근 구스는 조화해석과 조합론에 대한 연구를 진행하고 있습니다. 많은 연구가 유클리드 기하학의 미해결 문제인 카케야 문제(Kakeya 문제), 푸리에 분석의 제한된 유형 추정, 극단 조합론의 선 발생률 추정과 관련되어 있습니다.

                                                         1987년생 해석수론, 특히 소수론을 연구분야로 하는 영국의 수학자. 정수론에서 가장 유명한 문제 중 일부는 소수의 분포와 관련이 있습니다. 소수의 대규모 분포는 정수론의 정리(보다 정확하게는 리만 가설)를 따르지만, 많은 자연 문제는 짧은(또는 희소) 규모를 처리해야 합니다.

James Maynard는 2013년에 쌍둥이 소수 추측에 대한 중요한 결과를 달성했습니다. 그는 600보다 작은 간격의 소수 쌍이 무한하다는 것을 증명했습니다. 이 결과는 장이탕의 7천만 간격보다 작습니다. 그의 논문은 장이탕보다 반년 늦게 출판되었지만 그의 결과는 정수론 전문가들 사이에서 높은 평가를 받았습니다. Tao Zhexuan은 다음과 같이 말했습니다. "솔직히 그의 설명 방식은 나보다 더 깔끔합니다. 알고 보니 그의 진술이 약간 더 강한 것으로 나타났습니다."

Maynard의 방식은 우아하면서도 강력하며 충격적입니다. 선별이론의 경계를 무너뜨린다. 그리고 겉보기에는 반대 방향으로 그는 소수가 평균보다 훨씬 더 희박한 경우가 있다는 사실을 보여주었습니다. 이는 수십 년 동안 실질적인 진전이 없었던 유명한 Erdös 문제입니다.

Maynard는 또한 몬트리올 대학의 수학과 교수인 Koukoulopoulos와 함께 Duffin-Schaeffer 추측을 해결하는 디오판토스 근사 분야의 기초 작업을 수행했습니다. 1941년에 제안된 이 추측은 일반적인 실수가 유리수로 어떻게 근사화될 수 있는지 설명하는 힌친 정리의 최종 일반화로 간주될 수 있습니다.

2022년, 메이너드는 해석수 이론에 대한 공헌으로 필즈상을 수상했습니다. 필즈상은 수학계의 가장 권위 있는 상으로 흔히 수학계의 노벨상으로 여겨진다. 제임스 메이너드(James Maynard)는 소수의 구조와 디오판토스 근사법을 이해하는 데 상당한 진전을 가져온 분석수 이론에 대한 공헌으로 영광을 받았습니다.

2023년에 그는 수학 분야에서 또 다른 New Horizons Award를 수상했습니다.

리만 가설 등 세계 문제를 해결하는 두 수학자의 활약을 기대합니다.

참고링크:

https://www.jiqizhixin.com/articles/2019-01-12

https://www.zhihu.com/tardis/zm/ art/557594612

https://news.mit.edu/2014/profile-larry-guth-0527

^{https://mathstodon.xyz/@tao/112557248794707738}

^{https://zh.wikipedia.org/wiki/% E9% BB%8E% EBC%9% EBC%8% 9C% E6%83% B3}

위 내용은 리만 가설의 중요한 돌파구! 타오저쉬안(Tao Zhexuan)은 MIT와 옥스퍼드의 새로운 논문을 적극 추천했으며, 37세의 필즈상 수상자도 참여했다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!