역추적을 사용하여 여덟 여왕 문제 해결

여덟 여왕 문제는 두 여왕이 서로 공격할 수 없도록 체스판의 각 행에 여왕을 배치하는 해결책을 찾는 것입니다. 문제는 재귀를 사용하여 해결할 수 있습니다. 이번 장에서는 이 문제를 해결하기 위한 역추적이라는 일반적인 알고리즘 설계 기법을 소개하겠습니다. 역추적 접근 방식은 후보 솔루션을 점진적으로 검색하고,
후보가 유효한 솔루션이 될 수 없으며 새로운 후보를 찾습니다.

2차원 배열을 사용하여 체스판을 표현할 수 있습니다. 그러나 각 행에는 하나의 퀸만 있을 수 있으므로 1차원 배열을 사용하여 행에서 퀸의 위치를 ​​나타내는 것으로 충분합니다. 따라서 queens 배열을 다음과 같이 정의할 수 있습니다.

int[] 퀸즈 = 새로운 int[8];

j를 queens[i]에 할당하여 퀸이 i 행과 j 열에 배치됨을 나타냅니다. 아래 그림 (a)는 아래 그림 (b)의 체스판에 대한 queens 배열의 내용을 보여줍니다.

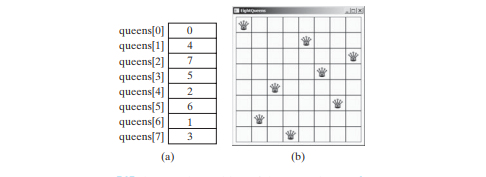
k = 0인 첫 번째 행부터 검색이 시작됩니다. 여기서 k는 고려 중인 현재 행의 인덱스입니다. 알고리즘은 _j = 0, 1, ... , 7에 대한 행의 j_번째 열에 여왕이 이 순서로 배치될 수 있는지 여부를 확인합니다. 검색은 다음과 같이 구현됩니다.

• 성공하면 다음 행의 여왕을 배치할 위치를 계속 검색합니다. 현재 행이 마지막 행이면 해결 방법을 찾습니다.
• 성공하지 못한 경우 이전 행으로 돌아가서 이전 행의 다음 열에서 새 게재위치를 계속 검색합니다.
• 알고리즘이 첫 번째 행으로 역추적하고 이 행에서 여왕에 대한 새로운 배치를 찾을 수 없는 경우 해결책을 찾을 수 없습니다.

아래 코드는 Eight Queens 문제에 대한 해결책을 표시하는 프로그램을 제공합니다.

package application;
import javafx.application.Application;
import javafx.geometry.Pos;
import javafx.stage.Stage;
import javafx.scene.Scene;
import javafx.scene.control.Label;
import javafx.scene.image.Image;
import javafx.scene.image.ImageView;
import javafx.scene.layout.GridPane;

public class EightQueens extends Application {
    public static final int SIZE = 8; // The size of the chess board
    // queens are placed at (i, queens[i])
    // -1 indicates that no queen is currently placed in the ith row
    // Initially, place a queen at (0, 0) in the 0th row
    private int[] queens = {-1, -1, -1, -1, -1, -1, -1, -1};

    @Override // Override the start method in the Application class
    public void start(Stage primaryStage) {
        search(); // Search for a solution

        // Display chess board
        GridPane chessBoard = new GridPane();
        chessBoard.setAlignment(Pos.CENTER);
        Label[][] labels = new Label[SIZE][SIZE];
        for(int i = 0; i < SIZE; i++)
            for(int j = 0; j < SIZE; j++) {
                chessBoard.add(labels[i][j] = new Label(), i, j);
                labels[i][j].setStyle("-fx-border-color: black");
                labels[i][j].setPrefSize(55, 55);
            }

        // Display queens
        Image image = new Image("file:C:/Users/Paul/development/MyJavaFX/src/application/image/lo.jpg");
        for(int i = 0; i < SIZE; i++)
            labels[i][queens[i]].setGraphic(new ImageView(image));

        // Create a scene and place it in the stage
        Scene scene = new Scene(chessBoard, 55 * SIZE, 55 * SIZE);
        primaryStage.setTitle("EightQueens"); // Set the stage title
        primaryStage.setScene(scene); // Place the scene in the stage
        primaryStage.show(); // Display the stage
    }

    public static void main(String[] args) {
        Application.launch(args);
    }

    /** Search for a solution */
    private boolean search() {
        // k - 1 indicates the number of queens placed so far
        // We are looking for a position in the kth row to place a queen
        int k = 0;
        while(k >= 0 && k < SIZE) {
            // Find a position to place a queen in the kth row
            int j = findPosition(k);
            if(j < 0) {
                queens[k] = -1;
                k--; // back track to the previous row
            } else {
                queens[k] = j;
                k++;
            }
        }

        if(k == -1)
            return false; // No solution
        else
            return true; // A solution is found
    }

    public int findPosition(int k) {
        int start = queens[k] + 1; // Search for a new placement

        for(int j =start; j < SIZE; j++) {
            if(isValid(k, j))
                return j; // (k, j) is the place to put the queen now
        }

        return -1;
    }

    /** Return true is a queen can be placed at (row, column) */
    public boolean isValid(int row, int column) {
        for(int i = 1; i <= row; i++)
            if(queens[row - i] == column // Check column
            || queens[row - i] == column - i // Check upleft diagonal
            || queens[row - i] == column + i) // Check upright diagonal
                return false; // There is a conflict
        return true; // No conflict
    }

}

프로그램은 search()(라인 20)을 호출하여 해결책을 검색합니다. 처음에는 어떤 행에도 퀸이 배치되지 않습니다(라인 16). 이제 검색은 k = 0(라인 53)으로 첫 번째 행에서 시작하여 여왕(라인 56)을 위한 장소를 찾습니다. 성공하면 행(61행)에 배치하고 다음 행(62행)을 고려합니다. 성공하지 못한 경우 이전 행(58~59행)으로 되돌아갑니다.

findPosition(k) 메소드는 queen[k] + 1부터 시작하여 k 행에 퀸을 배치할 수 있는 가능한 위치를 검색합니다(73행). ). start, start + 1, 에 퀸을 배치할 수 있는지 확인합니다. . . , 7 순서대로(75~78행). 가능하다면 열 인덱스를 반환합니다(77행). 그렇지 않으면 -1(80행)을 반환합니다.

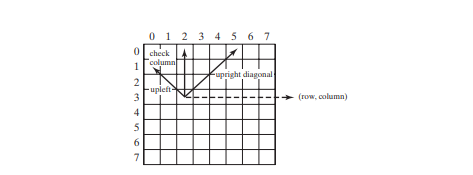
isValid(row, columns) 메서드는 지정된 위치에 퀸을 배치하면 이전에 배치된 퀸과 충돌이 발생하는지 확인하기 위해 호출됩니다(76행). 아래 그림과 같이 동일한 열(86행), 왼쪽 위 대각선(87행) 또는 오른쪽 위 대각선(88행)에 퀸이 배치되지 않도록 합니다.

위 내용은 역추적을 사용하여 여덟 여왕 문제 해결의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!