복합 재료의 원자 확산을 탐구하는 UC, 신경망 역학 방법 개발
- WBOY원래의
- 2024-06-19 05:04:39768검색

Editor | Green Luo
꽃향기가 바람에 퍼져 얼굴에 닿는 것처럼, 물질 속 원자와 분자도 '확산'을 겪고 있습니다.
재료의 분산은 침전, 새로운 상 형성 및 미세 구조 진화의 역학을 결정하며 기계적 및 물리적 특성에 큰 영향을 미칩니다. 복잡한 구성을 가진 재료의 고유한 화학적 복잡성으로 인해 원자 확산 모델링과 화학적으로 정렬된 구조의 형성에 어려움이 있습니다.
이와 관련하여 캘리포니아 대학의 연구원들은 복잡한 구성을 가진 재료의 원자 확산과 그에 따른 미세 구조 진화를 예측하기 위한 신경망 역학(NNK) 방법을 제안했습니다.
이 프레임워크는 효율적인 격자 구조와 화학적 특성화를 기반으로 하며 인공 신경망과 결합되어 모든 경로 종속 이동 장벽과 단일 원자 호핑을 정확하게 예측할 수 있습니다. 확장 가능한 NNK 프레임워크는 특별한 속성을 숨기는 광대한 조합 공간에서 확산 관련 속성을 탐색할 수 있는 유망한 새로운 길을 제공합니다.
"구성적으로 복잡한 물질의 확산 다중성과 화학적 순서를 탐색하기 위한 신경망 역학"이라는 제목의 관련 연구는 "Nature Communications"에 5월 9일 게재되었습니다.

재료 확산 및 모델링 과제
한 위치에서 다른 위치로 원자 이동 확산 이온의 수는 침전 및 상 핵형성과 같은 많은 중요한 과정과 거동을 제어합니다.
금속 및 합금에서 확산 과정은 결정 격자의 원자 호핑을 매개하는 공극 및 점 결함과 관련이 있습니다. 역장 또는 밀도 함수 이론을 기반으로 한 분자 역학(MD) 모델링은 나노초 시간 규모로 원자 확산 메커니즘을 조사할 수 있지만 느린 확산 역학으로 인한 미세 구조 변화는 종종 얻을 수 없습니다.
kMC 시뮬레이션 방법은 확산 매개 구조 진화를 시뮬레이션하는 데 사용되는 기술입니다. kMC 시뮬레이션에서는 전이 상태 검색의 계산 비용이 높기 때문에 주요 매개변수는 일반적으로 연속체 모델에서 매개변수화됩니다.
종종 고엔트로피 합금이라고도 불리는 조성 복합 합금(CCA)의 출현은 화학적 단거리 정렬, 석출, 분리 및 복사 결함 소멸을 비롯한 많은 흥미로운 동적 거동을 가져왔습니다. 이해와 최종 예측을 이해했습니다. 그러나 CCA의 화학적 복잡성은 확산 매개 프로세스의 모델링에 새로운 과제를 안겨줍니다.
기계 학습 방법의 출현은 비선형 상호 작용 및 대규모 조합 공간과 관련된 재료 과학의 계산적으로 복잡한 문제를 해결할 수 있는 잠재력을 보여주었습니다.
복잡한 조성을 갖는 합금의 공극 확산과 관련하여 중요한 핵심 매개변수는 확산 에너지 장벽 ΔE입니다. 이는 전이 상태와 초기 에너지 최소값 간의 에너지 차이입니다. 원자 규모의 조성 변동과 CCA의 다중 확산 방향 존재로 인해 벡터 특성, 특히 확산 경로 관련 잠재적 장벽을 정확하게 예측하려면 기계 학습 모델이 필요합니다.
Neural Network Dynamics Scheme
이 연구에서 연구자들은 복잡한 집중 화학 환경에서 확산으로 인한 화학 및 구조적 진화를 예측하고 시뮬레이션하기 위한 신경망 역학(NNK) 체계를 제안했습니다.
아래 그림은 공극이 있는 초기 원자 구성이 수치 매트릭스 또는 뉴런 다이어그램으로 인코딩된 격자 구조 및 화학적 표현입니다. 숫자(1, 2, 3)는 해당 원자 유형을 나타내고 0은 공석을 나타냅니다. 이러한 벡터화된 숫자는 NNK 모델에 전달되어 입력 뉴런으로 사용됩니다.
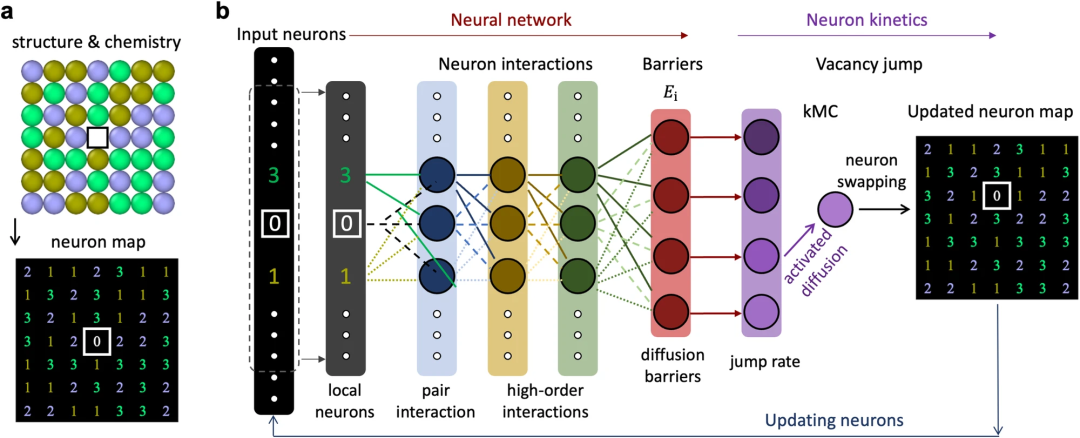
NNK는 인공신경망과 뉴런 역학 모듈로 구성됩니다. 도입된 신경망(숨겨진 레이어가 2개 이상)은 입력 뉴런(예: 원자 및 공석)과 출력 확산 에너지 장벽 간의 비선형 상호 작용을 학습하는 것을 목표로 합니다. 특히, 이 네트워크는 공석과 그 인접 뉴런만 입력으로 사용하므로 정확도를 희생하지 않고도 계산 비용이 낮고 일정합니다.
뉴런 역학 모듈은 운동 몬테카를로 방법을 사용하여 각 확산 경로와 관련된 사용 가능한 잠재적 장벽을 사용하여 확산 역학을 발전시킵니다. 원자 구성을 뉴런 그래프로 한 번만 변환하면 뉴런 그래프의 두 자리를 교환하여 공석 호핑 및 화학적 진화를 시뮬레이션할 수 있습니다. 이러한 방식으로 수백만 개의 갭 점프를 효율적으로 모델링할 수 있으며, 각 점프 반복은 단 두 개의 뉴런의 동작과 관련됩니다.
복잡한 구성을 가진 재료의 확산, 화학적 순서 탐색
NNK 및 bcc NbMoTa를 모델 시스템으로 사용하여 연구원들은 확산 동역학 매개 화학 순서 및 B2 상 형성을 탐색하고 CCA(확산 다중도)의 고유한 변칙적 확산을 밝혀냈습니다. .
B2(B2 단위 셀은 입방체의 모서리 또는 중앙에 정렬된 Ta와 Mo 두 물질로 구성된 단순한 bcc 구조를 가짐)의 순서가 최대에 도달하는 임계 온도의 존재를 발견했습니다. 화학적 순서의 온도 의존성은 기본 격자 호핑 확률성과 밀접한 관련이 있습니다.

녹는점에 가까운 고온에서 확산 점프는 결국 순전히 무작위 과정에 접근하며, 이는 낮은 질서 형성 경향에 해당합니다. 저온에서 격자 확산은 가장 낮은 장벽 경로에 의해 지배되며 방향성 호핑으로 나타나고 화학적으로 정렬된 구조의 핵 생성을 제한합니다. 중간 범위의 임계 온도에서는 무작위 및 방향성 격자 호핑이 시스템 전체에 퍼져 가장 높은 확산 이질성(다중성)을 나타냅니다.
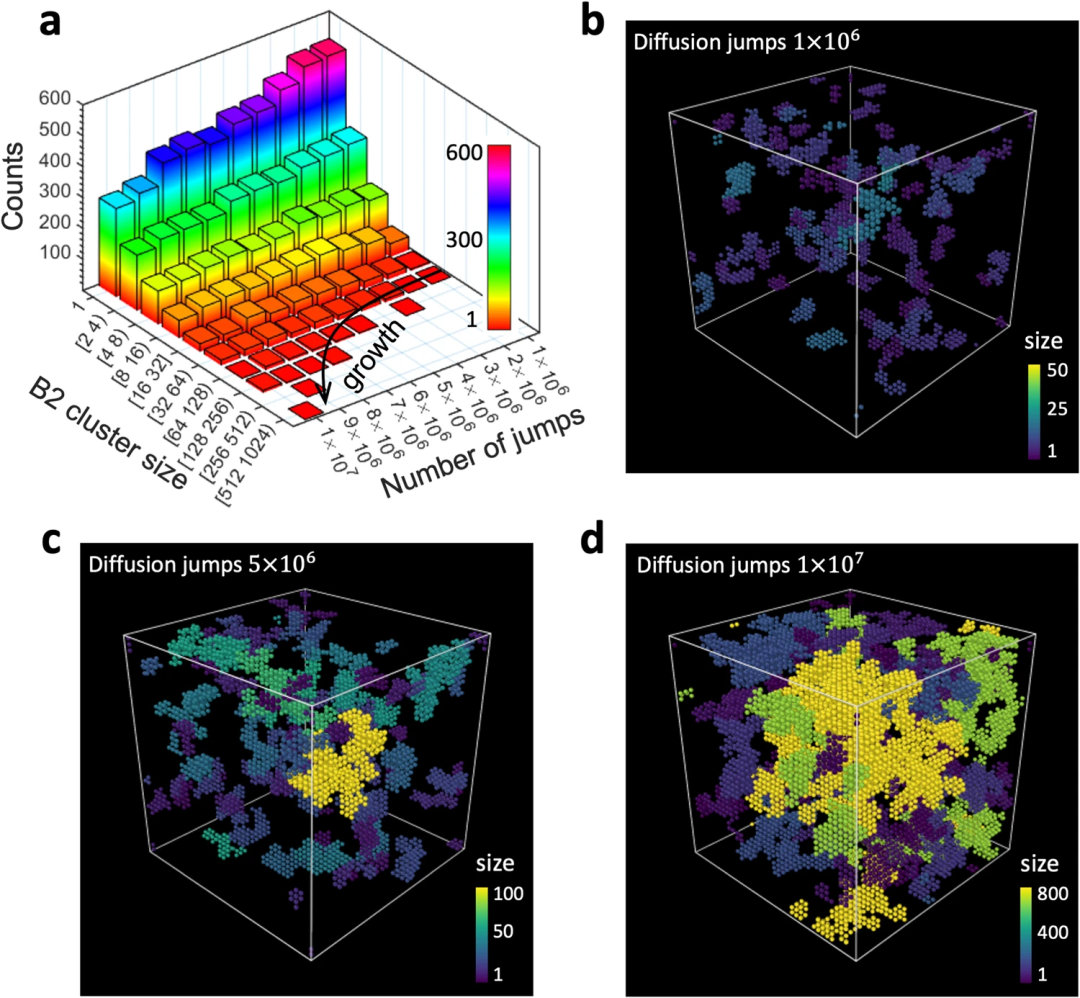
어닐링 과정에서 개별 B2 클러스터를 추적한 결과, 핵 생성 및 성장이 간헐적이고 불균일하며 작은 클러스터의 감소 및 소멸을 동반하는 것으로 나타났습니다. B2 구조의 운동적 성장의 이러한 특징은 무작위 원자 유형 교환을 사용한 가상 열역학 기반 모델링에서는 포착되지 않았으며 이는 보다 균일한 성장을 나타냈습니다.
이러한 결과는 핵 생성, 소멸, 성장 및 질서 있는 구조의 재배열과 같은 많은 과정이 상호 작용하고 조정되는 안정 상태를 향한 CCA의 복잡하고 수많은 운동 경로를 강조합니다.

수십 개의 구성 요소에 대해 훈련된 신경망은 보이지 않는 구성 요소에 대해 높은 성능을 보여 Nb-Mo-Ta의 전체 삼원 공간을 드러냅니다. 구성을 위한 디자인 공간은 거의 무제한이기 때문에 여러 요소를 혼합하여 형성된 구성적으로 복잡한 재료는 탐구할 새로운 영역을 열어줍니다.
다차원 구성을 확산 장벽 스펙트럼에 직접 연결함으로써 NNK는 탁월한 동적 특성이 숨겨져 있는 CCA의 광대한 구성 공간을 탐색하는 밝은 길을 제시합니다.
위 내용은 복합 재료의 원자 확산을 탐구하는 UC, 신경망 역학 방법 개발의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

