【原文:http://blog.pluskid.org/?p=682】 上一次介绍支持向量机,结果说到 Maximum Margin Classifier ,到最后都没有说“支持向量”到底是什么东西。不妨回忆一下上次最后一张图: 可以看到两个支撑着中间的 gap 的超平面,它们到中间的 separating hyper
【原文:http://blog.pluskid.org/?p=682】
上一次介绍支持向量机,结果说到 Maximum Margin Classifier ,到最后都没有说“支持向量”到底是什么东西。不妨回忆一下上次最后一张图:

可以看到两个支撑着中间的 gap 的超平面,它们到中间的 separating hyper plane 的距离相等(想想看:为什么一定是相等的?),即我们所能得到的最大的 geometrical margin
很显然,由于这些 supporting vector 刚好在边界上,所以它们是满足
当然,除了从几何直观上之外,支持向量的概念也会从其优化过程的推导中得到。其实上一次还偷偷卖了另一个关子就是虽然给出了目标函数,却没有讲怎么来求解。现在就让我们来处理这个问题。回忆一下之前得到的目标函数:
这个问题等价于(为了方便求解,我在这里加上了平方,还有一个系数,显然这两个问题是等价的,因为我们关心的并不是最优情况下目标函数的具体数值):
到这个形式以后,就可以很明显地看出来,它是一个凸优化问题,或者更具体地说,它是一个二次优化问题——目标函数是二次的,约束条件是线性的。这个问题可以用任何现成的 QP (Quadratic Programming) 的优化包进行求解。所以,我们的问题到此为止就算全部解决了,于是我睡午觉去了~ ![]()
啊?呃,有人说我偷懒不负责任了?好吧,嗯,其实呢,虽然这个问题确实是一个标准的 QP 问题,但是它也有它的特殊结构,通过 Lagrange Duality 变换到对偶变量 (dual variable) 的优化问题之后,可以找到一种更加有效的方法来进行求解——这也是 SVM 盛行的一大原因,通常情况下这种方法比直接使用通用的 QP 优化包进行优化要高效得多。此外,在推导过程中,许多有趣的特征也会被揭露出来,包括刚才提到的 supporting vector 的问题。
关于 Lagrange duality 我没有办法在这里细讲了,可以参考 Wikipedia 。简单地来说,通过给每一个约束条件加上一个 Lagrange multiplier,我们可以将它们融和到目标函数里去
然后我们令
容易验证,当某个约束条件不满足时,例如
这里用
当然,交换以后的问题不再等价于原问题,这个新问题的最优值用 ![]() 总之,第二个问题的最优值
总之,第二个问题的最优值
首先要让
带回
此时我们得到关于 dual variable
如前面所说,这个问题有更加高效的优化算法,不过具体方法在这里先不介绍,让我们先来看看推导过程中得到的一些有趣的形式。首先就是关于我们的 hyper plane ,对于一个数据点
这里的形式的有趣之处在于,对于新点
为什么非支持向量对应的
注意到如果 ![]()
嗯,于是呢,把所有的这些东西整合起来,得到的一个 maximum margin hyper plane classifier 就是支持向量机(Support Vector Machine),经过直观的感觉和数学上的推导,为什么叫“支持向量”,应该也就明了了吧?当然,到目前为止,我们的 SVM 还比较弱,只能处理线性的情况,不过,在得到了 dual 形式之后,通过 Kernel 推广到非线性的情况就变成了一件非常容易的事情了。不过,具体细节,还要留到下一次再细说了。 ![]()
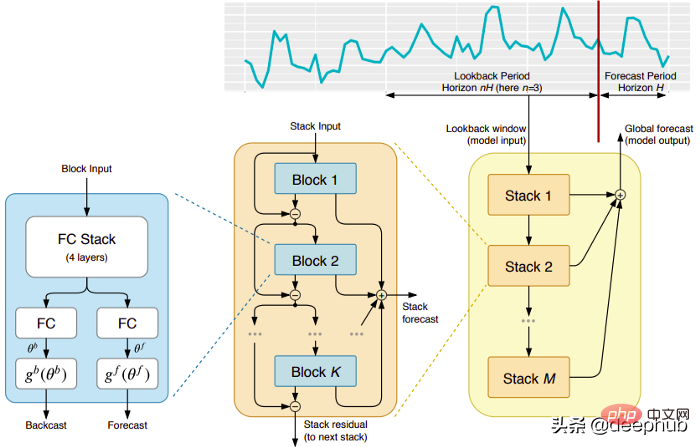 五个时间序列预测的深度学习模型对比总结May 05, 2023 pm 05:16 PM
五个时间序列预测的深度学习模型对比总结May 05, 2023 pm 05:16 PMMakridakisM-Competitions系列(分别称为M4和M5)分别在2018年和2020年举办(M6也在今年举办了)。对于那些不了解的人来说,m系列得比赛可以被认为是时间序列生态系统的一种现有状态的总结,为当前得预测的理论和实践提供了经验和客观的证据。2018年M4的结果表明,纯粹的“ML”方法在很大程度上胜过传统的统计方法,这在当时是出乎意料的。在两年后的M5[1]中,最的高分是仅具有“ML”方法。并且所有前50名基本上都是基于ML的(大部分是树型模型)。这场比赛看到了LightG
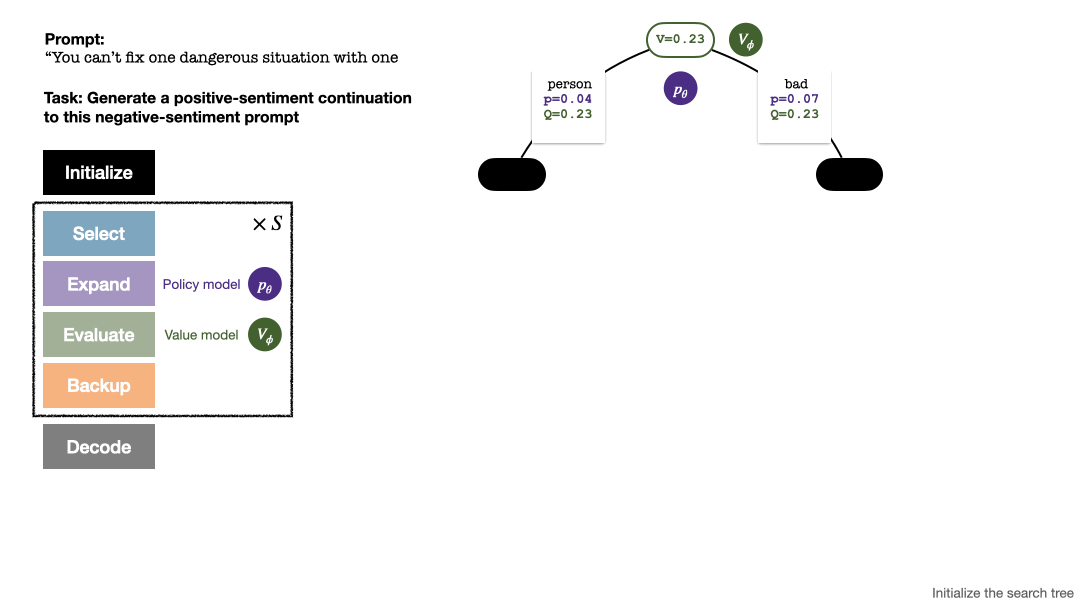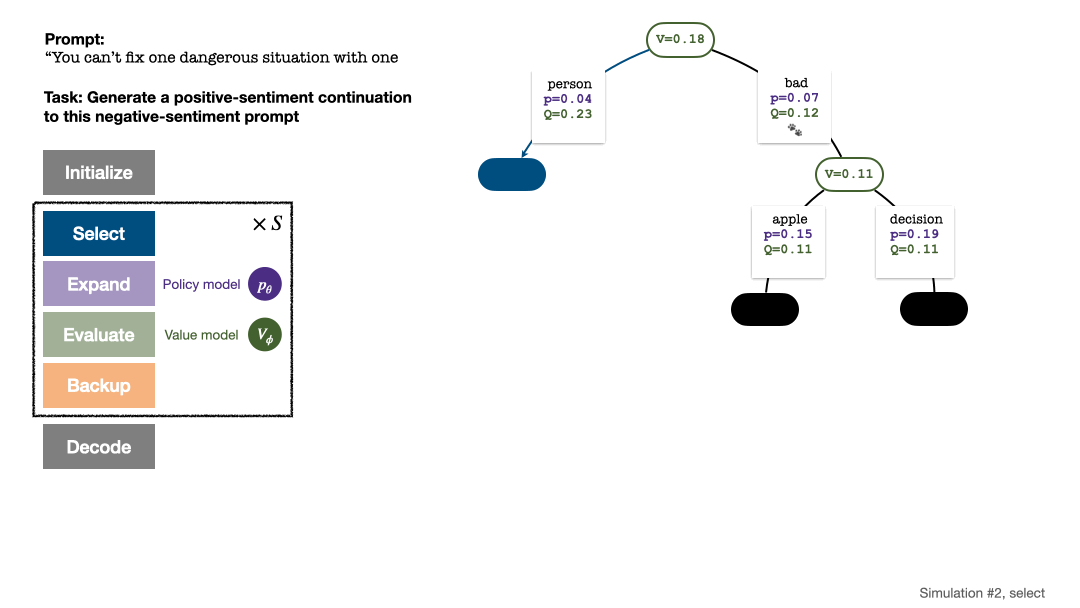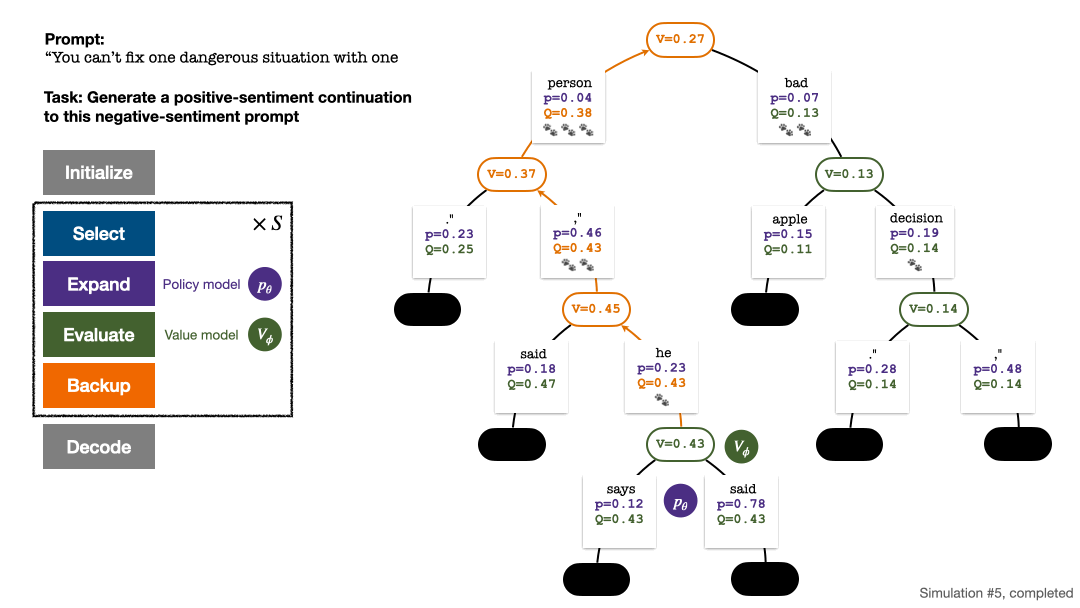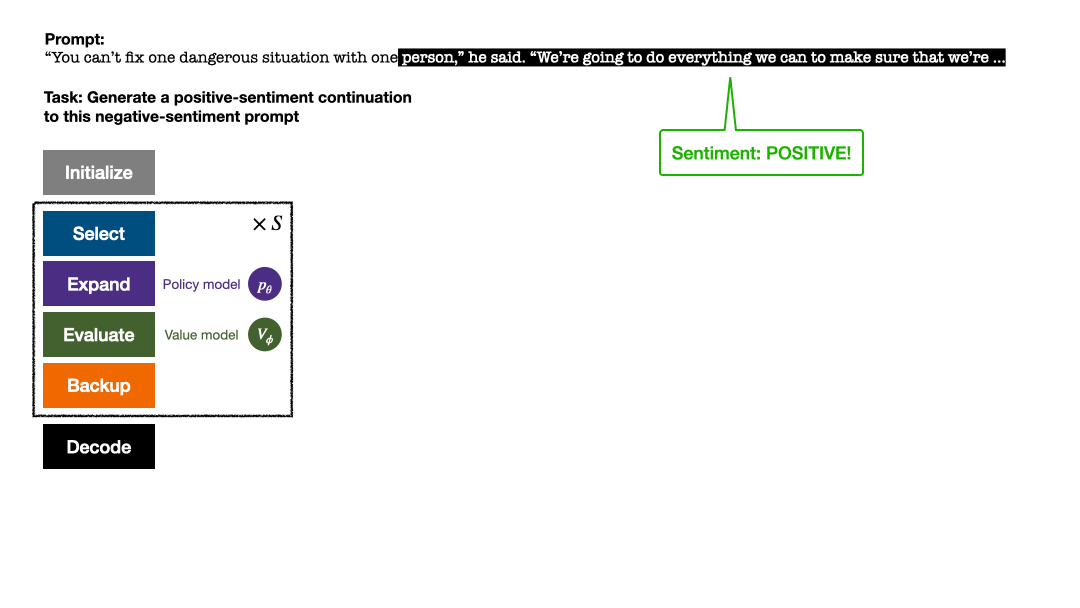 RLHF与AlphaGo核心技术强强联合,UW/Meta让文本生成能力再上新台阶Oct 27, 2023 pm 03:13 PM
RLHF与AlphaGo核心技术强强联合,UW/Meta让文本生成能力再上新台阶Oct 27, 2023 pm 03:13 PM在一项最新的研究中,来自UW和Meta的研究者提出了一种新的解码算法,将AlphaGo采用的蒙特卡洛树搜索算法(Monte-CarloTreeSearch,MCTS)应用到经过近端策略优化(ProximalPolicyOptimization,PPO)训练的RLHF语言模型上,大幅提高了模型生成文本的质量。PPO-MCTS算法通过探索与评估若干条候选序列,搜索到更优的解码策略。通过PPO-MCTS生成的文本能更好满足任务要求。论文链接:https://arxiv.org/pdf/2309.150
 MIT团队运用机器学习闭环自主分子发现平台,成功发现、合成和描述了303种新分子Jan 04, 2024 pm 05:38 PM
MIT团队运用机器学习闭环自主分子发现平台,成功发现、合成和描述了303种新分子Jan 04, 2024 pm 05:38 PM编辑|X传统意义上,发现所需特性的分子过程一直是由手动实验、化学家的直觉以及对机制和第一原理的理解推动的。随着化学家越来越多地使用自动化设备和预测合成算法,自主研究设备越来越接近实现。近日,来自MIT的研究人员开发了由集成机器学习工具驱动的闭环自主分子发现平台,以加速具有所需特性的分子的设计。无需手动实验即可探索化学空间并利用已知的化学结构。在两个案例研究中,该平台尝试了3000多个反应,其中1000多个产生了预测的反应产物,提出、合成并表征了303种未报道的染料样分子。该研究以《Autonom
 AI助力脑机接口研究,纽约大学突破性神经语音解码技术,登Nature子刊Apr 17, 2024 am 08:40 AM
AI助力脑机接口研究,纽约大学突破性神经语音解码技术,登Nature子刊Apr 17, 2024 am 08:40 AM作者|陈旭鹏编辑|ScienceAI由于神经系统的缺陷导致的失语会导致严重的生活障碍,它可能会限制人们的职业和社交生活。近年来,深度学习和脑机接口(BCI)技术的飞速发展为开发能够帮助失语者沟通的神经语音假肢提供了可行性。然而,神经信号的语音解码面临挑战。近日,约旦大学VideoLab和FlinkerLab的研究者开发了一个新型的可微分语音合成器,可以利用一个轻型的卷积神经网络将语音编码为一系列可解释的语音参数(例如音高、响度、共振峰频率等),并通过可微分神经网络将这些参数合成为语音。这个合成器
 Code Llama代码能力飙升,微调版HumanEval得分超越GPT-4,一天发布Aug 26, 2023 pm 09:01 PM
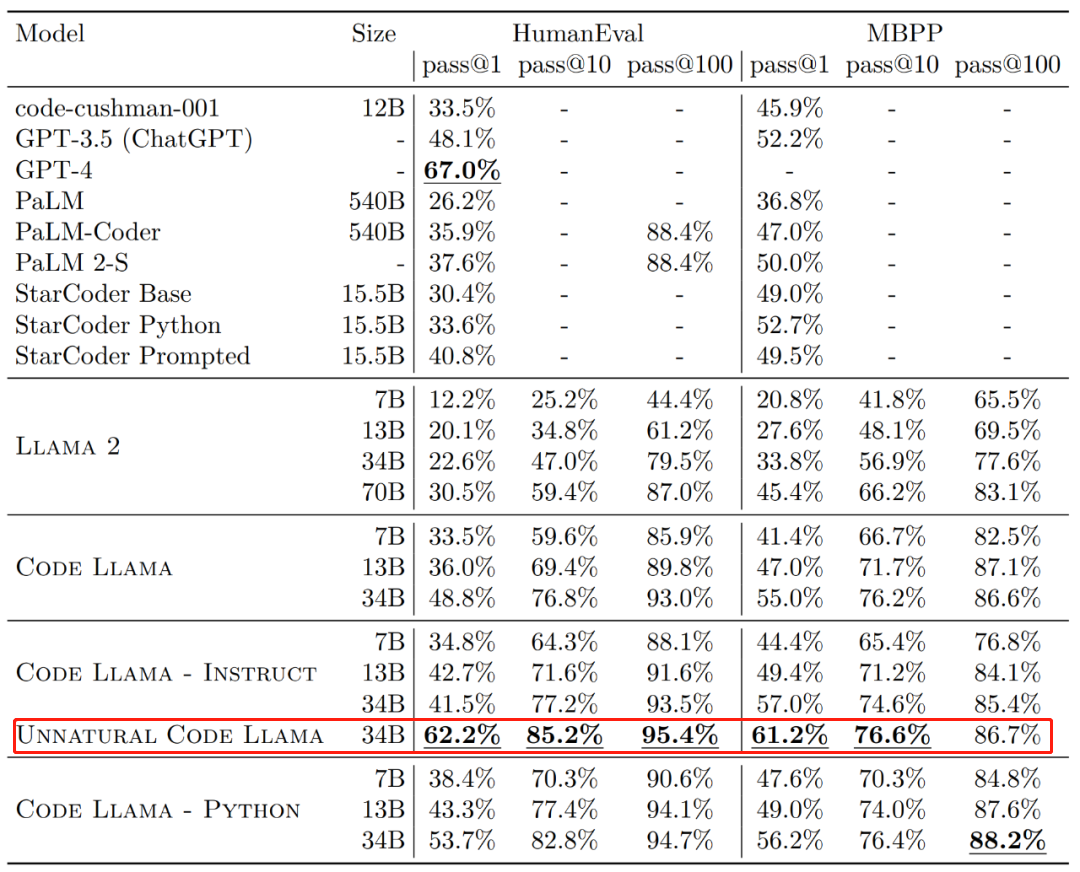
Code Llama代码能力飙升,微调版HumanEval得分超越GPT-4,一天发布Aug 26, 2023 pm 09:01 PM昨天,Meta开源专攻代码生成的基础模型CodeLlama,可免费用于研究以及商用目的。CodeLlama系列模型有三个参数版本,参数量分别为7B、13B和34B。并且支持多种编程语言,包括Python、C++、Java、PHP、Typescript(Javascript)、C#和Bash。Meta提供的CodeLlama版本包括:代码Llama,基础代码模型;代码羊-Python,Python微调版本;代码Llama-Instruct,自然语言指令微调版就其效果来说,CodeLlama的不同版
 准确率 >98%,基于电子密度的 GPT 用于化学研究,登 Nature 子刊Mar 27, 2024 pm 02:16 PM
准确率 >98%,基于电子密度的 GPT 用于化学研究,登 Nature 子刊Mar 27, 2024 pm 02:16 PM编辑|紫罗可合成分子的化学空间是非常广阔的。有效地探索这个领域需要依赖计算筛选技术,比如深度学习,以便快速地发现各种有趣的化合物。将分子结构转换为数字表示形式,并开发相应算法生成新的分子结构是进行化学发现的关键。最近,英国格拉斯哥大学的研究团队提出了一种基于电子密度训练的机器学习模型,用于生成主客体binders。这种模型能够以简化分子线性输入规范(SMILES)格式读取数据,准确率高达98%,从而实现对分子在二维空间的全面描述。通过变分自编码器生成主客体系统的电子密度和静电势的三维表示,然后通
 手机摄影技术让以假乱真的好莱坞级电影特效视频走红Sep 07, 2023 am 09:41 AM
手机摄影技术让以假乱真的好莱坞级电影特效视频走红Sep 07, 2023 am 09:41 AM一个普通人用一台手机就能制作电影特效的时代已经来了。最近,一个名叫Simulon的3D技术公司发布了一系列特效视频,视频中的3D机器人与环境无缝融合,而且光影效果非常自然。呈现这些效果的APP也叫Simulon,它能让使用者通过手机摄像头的实时拍摄,直接渲染出CGI(计算机生成图像)特效,就跟打开美颜相机拍摄一样。在具体操作中,你要先上传一个3D模型(比如图中的机器人)。Simulon会将这个模型放置到你拍摄的现实世界中,并使用准确的照明、阴影和反射效果来渲染它们。整个过程不需要相机解算、HDR
 谷歌用大型模型训练机器狗理解模糊指令,激动不已准备去野餐Jan 16, 2024 am 11:24 AM
谷歌用大型模型训练机器狗理解模糊指令,激动不已准备去野餐Jan 16, 2024 am 11:24 AM人类和四足机器人之间简单有效的交互是创造能干的智能助理机器人的途径,其昭示着这样一个未来:技术以超乎我们想象的方式改善我们的生活。对于这样的人类-机器人交互系统,关键是让四足机器人有能力响应自然语言指令。近来大型语言模型(LLM)发展迅速,已经展现出了执行高层规划的潜力。然而,对LLM来说,理解低层指令依然很难,比如关节角度目标或电机扭矩,尤其是对于本身就不稳定、必需高频控制信号的足式机器人。因此,大多数现有工作都会假设已为LLM提供了决定机器人行为的高层API,而这就从根本上限制了系统的表现能


핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

MinGW - Windows용 미니멀리스트 GNU
이 프로젝트는 osdn.net/projects/mingw로 마이그레이션되는 중입니다. 계속해서 그곳에서 우리를 팔로우할 수 있습니다. MinGW: GCC(GNU Compiler Collection)의 기본 Windows 포트로, 기본 Windows 애플리케이션을 구축하기 위한 무료 배포 가능 가져오기 라이브러리 및 헤더 파일로 C99 기능을 지원하는 MSVC 런타임에 대한 확장이 포함되어 있습니다. 모든 MinGW 소프트웨어는 64비트 Windows 플랫폼에서 실행될 수 있습니다.

Atom Editor Mac 버전 다운로드
가장 인기 있는 오픈 소스 편집기

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

mPDF
mPDF는 UTF-8로 인코딩된 HTML에서 PDF 파일을 생성할 수 있는 PHP 라이브러리입니다. 원저자인 Ian Back은 자신의 웹 사이트에서 "즉시" PDF 파일을 출력하고 다양한 언어를 처리하기 위해 mPDF를 작성했습니다. HTML2FPDF와 같은 원본 스크립트보다 유니코드 글꼴을 사용할 때 속도가 느리고 더 큰 파일을 생성하지만 CSS 스타일 등을 지원하고 많은 개선 사항이 있습니다. RTL(아랍어, 히브리어), CJK(중국어, 일본어, 한국어)를 포함한 거의 모든 언어를 지원합니다. 중첩된 블록 수준 요소(예: P, DIV)를 지원합니다.






