如果是一个非常大的N <10000000 那么计算出来的N!也是非常大的,现在只需要知道最高位的数字。
通过斯特林公式可以计算。
特林斯公式: (公式1)
(公式1)
如下是算法:
result = 0.5* log(2*PI*(double)n)/log(10.0) + (double)n* log((double)n/E)/log(10.0);
result -= (int)result;
first_number = exp(result * log(10.0));
以上算法代码计算通过公式表示: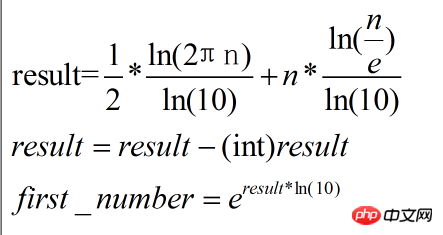 (公式2)
(公式2)
目前已知通过如下计算可以得到最高位: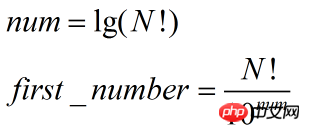 (公式3)
(公式3)
剩下的就是求N!,虽然N!可以通过特林斯计算,但是计算结果非常大。计算机直接计算会溢出结果,如下执行结果: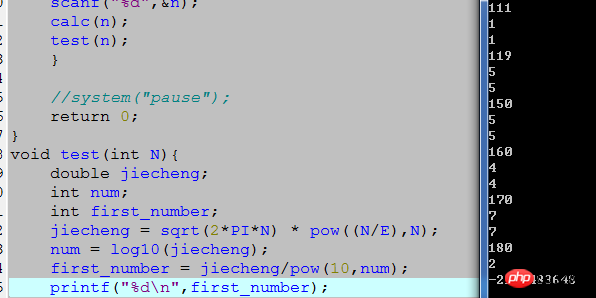
可以看出当执行到180的时候结果都已经溢出。
原因应该是在计算N! 的时候结果直接存储在计算机导致空间不足。
我所不明白的是为什么(公式2)的算法就可以直接计算出结果不溢出,且正确(当然数字过小的话也会有错误,比如0,1,2,3,7,8结果将不正确)。
迷茫2017-04-17 13:57:29
最终是通过以10为底的对数log10(xxx)来求其最高位,这个你理解吧?他上面就是通过对数变换把求以10为底的对数转为以e为底的对数 aka: ln(yyy)
ringa_lee2017-04-17 13:57:29
首先,胡须佬头,已经说的很明白了,原理就是他所说的那个,把原来用lg去求的问题,转换为了ln去求。
我还是给你贴张tu吧:(喜欢数学的都是好样的)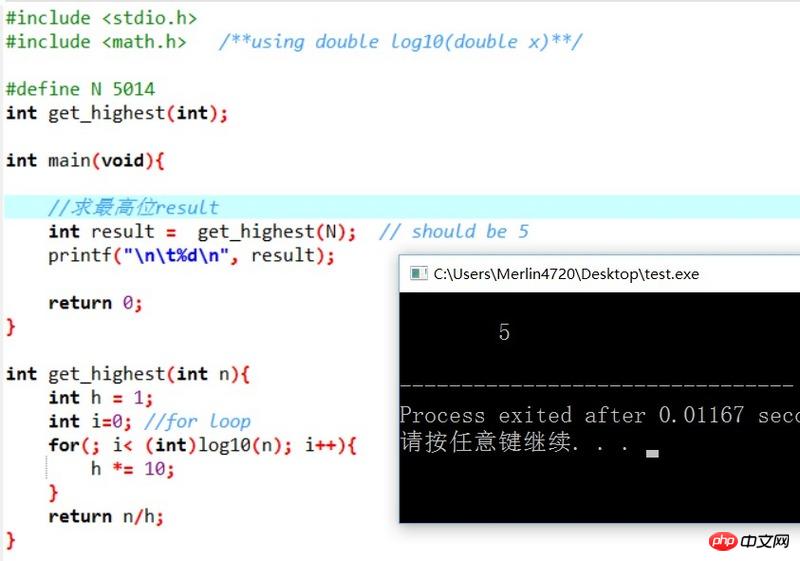
看到啦,其实上面已经验证过了,如果要求5014的最高位,那么可以写成:
最高位 = 5014 / (取整数)1g(5014); (注意类C语言里面,除法,会进行整型截断)
ok,再说正事儿,你那个特林斯公式,假设拿到的阶乘的近似值为X (一大串不管了,简单点儿叫X),
如果想拿到这个数的最高位h,那么有如下计算:
h = X / (int)lgX;
此时,通过特林斯公式,X 已求得,
计算一下“lgX的整数部分”就可以了。
先笼统的算(先不求整部和小数部分,直接算lgX)
lgX = lnX / ln10 (就是你上面把特林斯公式带进去求值的那个式子,哦,你的图还算错了)
得到lgX= result (我化简过了,不信你把那个特林斯公式化简成)
到这里,就明白了,拿到result的整数部分,就能救出lgX的整数部分了,也就能求出最高位h.
而不是你说的“拿到小数部分”。
最后,根据你提供的特林斯公式,得到阶乘factorial的值为:
X 约等于 e^(ln10 * result的整数部分); (你可以自己从特林斯的公式变形到这一步看看)
貌似也不是你所说的
first_number = exp(result * log(10.0));
再有问题,在讨论?贴出你最终的结果?