此题被称为“世上最有心机的面试题”
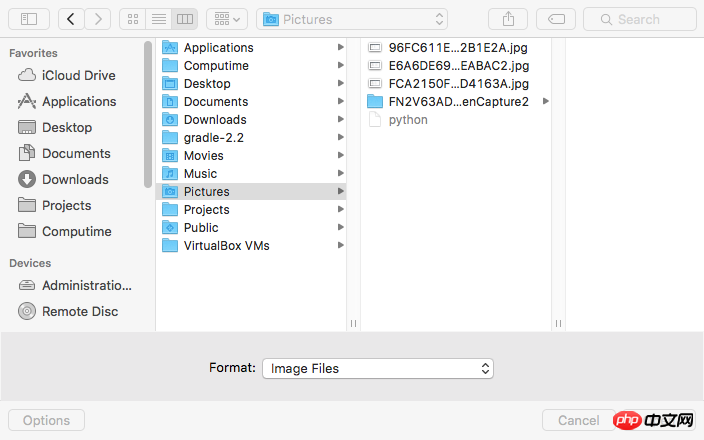
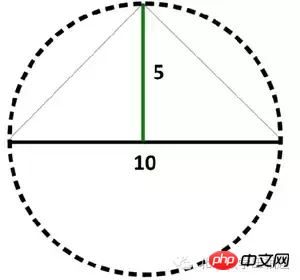
假设有一个直角三角形,斜边长10cm,从顶点到斜边作垂线,垂线长6cm(如下图所示),求直角三角形的面积
是不是很简单
有8个球,其中1个比另外的要略重。在不用砝码的前提下,你最少要称几次,才能找出这个球?
PHP中文网2017-04-11 11:04:58
第一题是高中很常见的题吧。
∵ 圆的直径所对的圆周角是直角。
∴ △ABC三点所在圆的半径是5,且直线AB是直径。
∵ CD是圆上的点向直径做垂线
∴ CD ≤ 半径,即 CD ≤ 5
∴ 这与题目矛盾,所以题目错误。
第二题简直送分……最少次数,那当然就是两次了。
眼拙了,这个题目没有要求一定,所以,运气好的话,最少1次就可以了。
如果加上了这个限定词,最少需要2次。
ringa_lee2017-04-11 11:04:58
这个是被采纳同学的课外扩展 里面的内容也挺好的
答案揭晓:连接在这里,里边还有
根本不存在这么一个直角三角形!
直角三角形斜边所对的角是直角,因此,假设其斜边是一个圆的直径,其顶点就可能在圆周的任何一个点上。如果要作一条垂直于斜边的线,那就一定是垂直于圆的直径的线,也就是说,这条线是圆的半径,长度为5cm。
最少称两次:把所有的球分成三组,其中两组每组3个球,另一组2个球;首先,将3个球的两组进行称重,如果其中一组比较重,从这组球当中任选两个,再次称重,如果轻重不等,重的球就是你要找的。如果轻重相等,剩下那个球就是你要找的。如果第一次称重时两组球一样重,那么就把剩下一组的两个球进行称重,就能得到答案。
迷茫2017-04-11 11:04:58
看大家都回答两次,但都没说原因啊...
感觉第二题,楼上也说了不是一定的话,一次,碰运气刚好称出来。如果一定的话是最少两次,分法是3:3:2。
噗,竟然还被踩了...理由是啥?
天蓬老师2017-04-11 11:04:58
第一题上当了,看半夏说不可能
根据三角形面积有:
$$S=AC*BC/2 = AB*CD/2 = 6*10/2$$
得出
$$AC*BC=60$$
根据直角三角形勾股定理有:
$$AC^2+BC^2 =AB^2= 100$$
构造一个平方$$(AC−BC)^2$$展开有
$${(AC-BC)^2 = AC^2-2*AC*BC+BC^2 = -20}$$
一个实数的平方数不能小于0
第二题:两次找出这个球
PHP中文网2017-04-11 11:04:58
第一题假使题目改为垂线长为5cm的话,其实坑点是一共有三个直角三角形啊,你们就只算那个最大的么;
第二题如果题目的意思不是‘最少称几次一定能找出才能找出这个球’(’注意是‘一定’)的话,那么称一次就够了(拿两个球称,如果运气够好,刚好拿到了那个略重的球);如果是要‘一定’能找出的话,最少要称三次吧,反正我就只想到三次:用二分法,把球不断分成两份,直至只剩两个球,重的那个就是所求的球。两次是用什么方法?