小規模な言語モデルの登場は、大規模な言語モデルの高価なトレーニングと推論の欠点を補うものですが、ある段階(飽和状態)までトレーニングするとパフォーマンスが低下するという事実もあります。現象)では、この現象の原因は何でしょうか?それを克服して、小さな言語モデルのパフォーマンスを向上させるために活用できるでしょうか?
言語モデリングの分野における最新の進歩は、非常に大規模な Web テキスト コーパス上で高度にパラメータ化されたニューラル ネットワークを事前トレーニングすることにあります。実際には、このようなモデルをトレーニングと推論に使用するとコストが高くなる可能性があり、より小規模な代替モデルの使用が求められます。ただし、小規模なモデルでは飽和が発生し、トレーニングのある程度の進んだ段階で能力の低下と頭打ちを特徴とする現象が発生する可能性があることが観察されています。
最近の論文では、この飽和和現象が、より小さいモデルの潜在次元とターゲット コンテキスト確率分布の上位ランクの間の不一致によって説明できることがわかりました。この不一致は、いわゆるソフトマックス ボトルネックを採用することにより、これらのモデルで使用される線形予測ヘッドのパフォーマンスに影響を与えます。

論文リンク: https://arxiv.org/pdf/2404.07647.pdf
この記事では、さまざまな設定におけるソフトマックスのボトルネックの影響を測定します。そして、1000 未満の隠れ次元に基づくモデルは、事前トレーニングの後半段階で劣化した潜在表現を採用する傾向があり、その結果、評価パフォーマンスが低下することがわかりました。
はじめに
表現劣化問題は、テキスト データの自己教師あり学習方法などのさまざまなモードに影響を与える一般的な現象です。言語モデルの中間表現を観察すると、その低角度の変動性 (または異方性)、またはトレーニング中に生じる異常な次元が明らかになります。ただし、これらの観察は主に、BERT や GPT-2 などのファミリー モデルと同等の寸法を持つ比較的小規模なモデルで行われます。
これらのモデルは通常、トークン シーケンス

を受け入れ、比較的低次元の R^d コンテキスト表現を生成するニューラル ネットワーク f_θ で構成されます。 d はモデルの隠れ次元です。次に、コンテキスト トークンの確率の対数を生成する言語モデリング ヘッドに依存します。言語モデリング ヘッドの一般的な選択は、パラメーター W ∈ R^(V×d) を持つ線形層です。ここで、V は可能なトークンの数です。したがって、次のトークンの結果の確率分布は  になります。ここで、σ はソフトマックス関数です。
になります。ここで、σ はソフトマックス関数です。
言語モデリングの分野では、現在の傾向は GPT-2 によって導入された生成事前トレーニング手法を拡張することです。これは、Web テキストの巨大なコーパス上で数十億のパラメーターで構成されるニューラル モデルをトレーニングすることを意味します。ただし、これらの高度にパラメーター化されたモデルをトレーニングして適用すると、エネルギーとハードウェア関連の問題が発生するため、より小さなモデルで同様のパフォーマンス レベルを達成する方法を見つける必要があります。
ただし、Pythia モデル スイートの評価では、非常に大規模なコーパスで小さなモデルをトレーニングすると飽和につながる可能性があり、事前トレーニングの後半でパフォーマンスが低下することで明らかになります。この論文は、表現劣化のレンズを通してこの飽和現象を調査し、2 つの現象の間に強い相関関係があることを発見します。さらに、表現劣化が小さなモデルの言語モデリング ヘッドで発生し、上記で理論的にも経験的にも証明されていることを示します。線形言語モデリングのヘッダーが、小さな隠れ次元に基づくアーキテクチャのパフォーマンスのボトルネックになる可能性があります。
言語モデルの飽和現象
この記事では、Pythia チェックポイントは言語モデルの飽和状態にある唯一のリリースであるため、そのパフォーマンスの飽和を実際に観察して定量化できることを最初に検証します。モデルサイズの確認ポイント。この論文では、トレーニング前のデータセット (つまり、The Pile) からランダムにサンプリングされた 50,000 個のトークンに対する Pythia チェックポイントのクロス エントロピーを測定します。
図 1a では、4 億 1,000 万のパラメーター モデルでも飽和状態に陥っていることがはっきりとわかります。これは、高度なトレーニング段階でのドメイン内損失の増加によって明らかです。

図 1b では、この論文は Hoffmann et al (2022) の方法に従って 4 億 1,000 万のパラメーターから開始してモデルのデータ ポイントをフィッティングし、モデルのみを最適化します。 -依存定数 (A および α)、他のすべての値 (B = 410.7、β = 0.28、E = 1.69) を再利用します。ここでは、Hoffmann et al (2022) によって与えられたパラメータ数 N とトークン数 T の関係を確認します。
この論文では、最適なパラメーターは A = 119.09 および α = 0.246 であることがわかります。著者らは、最適なチェックポイントと最終的なチェックポイントに対応するトークン数の近似曲線を示しています。最終チェックポイントのパフォーマンスは、外挿値より平均して約 8% 低いことがわかります。損失を最小化する (最適な) チェックポイントは、学習率の冷却が不完全であるため、外挿法よりも低いことが予想されましたが、そのパフォーマンスは外挿法よりも約 4% 低いだけでした。
表 1 に示すように、言語モデル評価ツール (LM 評価ハーネス) の評価に使用したデータセットでも、同様のパフォーマンス飽和現象が観察されました。

#パフォーマンスの飽和はランクの飽和です
スケール異方性
異方性は一般的ですさまざまな小規模言語モデルで観察される表現劣化の形式。これは、特定の層における表現分布の角度変動の減少から構成されます。以前の研究 (Ethayarajh、2019; Godey et al.、2024) では、小さな変形言語モデルのほぼすべての層が異方性であることが指摘されています。一連のベクトル表現 H の異方性を測定する一般的な方法は、平均コサイン類似度: モデルです。この問題を解決するために、この論文では、一連のモデル中間表現、つまり GPT-2、OPT、Pythia、および Gemma のレイヤー間の平均コサイン類似度を計算します。このデータセットのドメインには、これらのスイートで使用される事前トレーニングされたデータセットのドメインが含まれるか一致すると想定されているため、この記事では The Pile のサブサンプルを使用します。 図 2 では、ほとんどの Transformer モデルのほとんどの層が、スケールに関係なく、ある程度異方性であることがわかります。ただし、最後の層には、モデルがほぼ等方性であるか、高度に異方性であるかの二分法があるようです。この論文では、この二分法が Pythia スイートの飽和現象の 1 つと一致していることに注目しています。つまり、1 億 6,000 万以下のパラメータを持つモデルのみが最後の層の異方性の影響を受けるということです。

特異値飽和
平均コサイン類似度は分布の均一性を測る貴重な尺度ですが、他の指標を含めることで、特定の多様体の複雑さをより適切に捉えることができます。さらに、言語モデルの出力埋め込みのみに焦点を当てており、その重みには焦点を当てていません。このセクションでは、言語モデリング ヘッドの特異値分布を研究することでこの論文の分析を拡張し、経験的な観察をこの論文の理論的発見に結び付けます。
図 4 は、トレーニング中の最終予測層の重み W に沿った特異値分布を示しています。
図 4 は、発生するスペクトル飽和の特定のパターンを示しています。パフォーマンスが飽和するのとほぼ同時に。この図は、特異値分布がトレーニング中に徐々に平坦になり、ほぼ均一に達した後、突然、他の分布に比べて最大の特異値が相対的に高いとがった分布に発展することを示しています。 この動作をより正確に定量化するために、この記事では、正規化された特異値分布と一様分布の間のカルバック ライブラー発散として計算される特異エントロピー メトリックを使用します。 図 5 は、4 億 1,000 万個未満のパラメーターを使用するモデルと、より大きなパラメーターを使用するモデルで特異分布がどのように異なる展開をするかを示しています。小さなモデルの先頭では、特異値の分布が徐々に均一になっていき、最終的には突然劣化することがわかります。これは、やはり言語モデルのパフォーマンスの低下と相関関係があります。大きなモデルの特異値分布はより安定する傾向があり、トレーニング全体を通じて明らかな単調パターンを示しません。
図 5 は、4 億 1,000 万個未満のパラメーターを使用するモデルと、より大きなパラメーターを使用するモデルで特異分布がどのように異なる展開をするかを示しています。小さなモデルの先頭では、特異値の分布が徐々に均一になっていき、最終的には突然劣化することがわかります。これは、やはり言語モデルのパフォーマンスの低下と相関関係があります。大きなモデルの特異値分布はより安定する傾向があり、トレーニング全体を通じて明らかな単調パターンを示しません。
Softmax のボトルネックと言語の次元

直感的 言い換えれば、上で観察された特異値分布の飽和現象は、より小型のモデルにのみ当てはまり、LM ヘッドの最適化に含まれる寸法に疑問が生じます。このセクションでは、LM ヘッドのランクの臨界値を経験的に測定し、このヘッドの出力が一致する必要があるコンテキスト確率分布の次元を推定することを提案します。
線形ヘッド ランクの影響を経験的に測定するために、この論文では、高度にパラメーター化された言語モデルから派生した事前トレーニング済みのコンテキスト表現でランク制限されたヘッドをトレーニングすることを提案します。最大ランク r を制御するには、W = AB ∈ R^(V×d) の形式のヘッドを考慮します。ここで、A ∈ R^(V×r) と B ∈ R^(r×d) の係数は次から始まります。 N(0 ,1) が抽出されました (d はモデルの隠れ次元です)。この W 行列のランクは、パラメーター r ∈ [1, d] によって制限された値の範囲にわたってスキャンされます。
言語モデルをフリーズし、ランク制限されたヘッドを約 1 億 5,000 万のトークンでトレーニングしながら、トレーニング可能なパラメーターの数に適応するように学習率を調整します。
図 6 では、モデルのサイズに関係なく、言語モデリング ヘッド W のランクが 1000 を下回ると、複雑さが大幅に減少し始めることがわかります。これは、隠れ次元が大きいモデルの場合、ヘッドはパフォーマンスの大きなボトルネックではありませんが、隠れ次元が小さいモデルの場合、出力表現の品質とは無関係にパフォーマンスに悪影響を与える可能性があることを意味します。

もう 1 つの興味深い要素は、推定データ自体の固有の次元です。特定の帰納的バイアスに関連する可能性のある影響を回避するために、この論文では、2 つの異なる語彙サイズ (30,000 個のトークン) を使用して、対象範囲が異なる複数のデータセット (IMDb、Wikitext、および The Pile) で単純な 5 グラム言語モデルをトレーニングしました。 Llama-2、Pythia 用 50,000 トークン)。 C が観測された 5 グラムを前提として、この論文では行列 W ∈ R^(C×V) を考慮します。ここで、各行は、4 つのトークンが与えられた場合に考えられるトークンの確率分布であり、Terashima (2003) のように、それらの特異値分布を計算します。
図 7 は、エッカート・ヤング・ミルスキーの定理 (補題 5.2 を参照) によって予測され、W ノルムのフロベニウスに正規化されたランク d の行列 W の最小近似誤差である W 誤差を報告します。


#理論上のボトルネック
同時に、W の推定ランクは次のとおりです。隠れた次元と同じオーダーの大きさであり、比較において無視することはできません。ここでは、理論的な観点から、理想的な線形言語モデリング ヘッドの寸法とパフォーマンスの関係を分析します。 このセクションの目的は、コンテキスト分布の固有の次元と、言語モデルの出力表現の低次元に起因する可能性のあるパフォーマンスのボトルネックとの間の正式な関連性を特定することです。この目的を達成するために、理想的なコンテキスト表現に基づいて最適化された言語モデリング ヘッドが考案され、そのスペクトル特性と、同じ表現で低ランクのヘッドをトレーニングしたときに生じるパフォーマンス ギャップとの関係が調査されます。 研究の詳細については、元の論文をご覧ください。以上が小型モデルのパフォーマンスが飽和してパフォーマンスが低下する根本原因はソフトマックスにありますか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 踊りましょう:私たちの人間のニューラルネットを微調整するための構造化された動きApr 27, 2025 am 11:09 AM
踊りましょう:私たちの人間のニューラルネットを微調整するための構造化された動きApr 27, 2025 am 11:09 AM科学者は、彼らの機能を理解するために、人間とより単純なニューラルネットワーク(C. elegansのものと同様)を広く研究してきました。 ただし、重要な疑問が生じます。新しいAIと一緒に効果的に作業するために独自のニューラルネットワークをどのように適応させるのか
 新しいGoogleリークは、Gemini AIのサブスクリプションの変更を明らかにしますApr 27, 2025 am 11:08 AM
新しいGoogleリークは、Gemini AIのサブスクリプションの変更を明らかにしますApr 27, 2025 am 11:08 AMGoogleのGemini Advanced:Horizonの新しいサブスクリプションティア 現在、Gemini Advancedにアクセスするには、1か月あたり19.99ドルのGoogle One AIプレミアムプランが必要です。 ただし、Android Authorityのレポートは、今後の変更を示唆しています。 最新のGoogle p
 データ分析の加速がAIの隠されたボトルネックをどのように解決しているかApr 27, 2025 am 11:07 AM
データ分析の加速がAIの隠されたボトルネックをどのように解決しているかApr 27, 2025 am 11:07 AM高度なAI機能を取り巻く誇大宣伝にもかかわらず、エンタープライズAIの展開内に大きな課題が潜んでいます:データ処理ボトルネック。 CEOがAIの進歩を祝う間、エンジニアはクエリの遅い時間、過負荷のパイプライン、
 MarkitDown MCPは、任意のドキュメントをマークダウンに変換できます!Apr 27, 2025 am 09:47 AM
MarkitDown MCPは、任意のドキュメントをマークダウンに変換できます!Apr 27, 2025 am 09:47 AMドキュメントの取り扱いは、AIプロジェクトでファイルを開くだけでなく、カオスを明確に変えることです。 PDF、PowerPoint、Wordなどのドキュメントは、あらゆる形状とサイズでワークフローをフラッシュします。構造化された取得
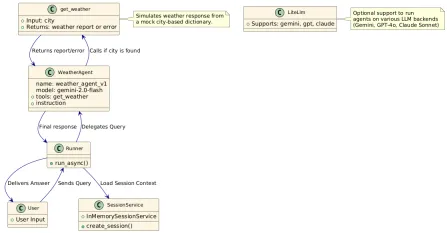 建物のエージェントにGoogle ADKを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:42 AM
建物のエージェントにGoogle ADKを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:42 AMGoogleのエージェント開発キット(ADK)のパワーを活用して、実際の機能を備えたインテリジェントエージェントを作成します。このチュートリアルは、ADKを使用して会話エージェントを構築し、GeminiやGPTなどのさまざまな言語モデルをサポートすることをガイドします。 w
 効果的な問題解決のためにLLMを介したSLMの使用 - 分析VidhyaApr 27, 2025 am 09:27 AM
効果的な問題解決のためにLLMを介したSLMの使用 - 分析VidhyaApr 27, 2025 am 09:27 AMまとめ: Small Language Model(SLM)は、効率のために設計されています。それらは、リソース不足、リアルタイム、プライバシーに敏感な環境の大手言語モデル(LLM)よりも優れています。 特にドメインの特異性、制御可能性、解釈可能性が一般的な知識や創造性よりも重要である場合、フォーカスベースのタスクに最適です。 SLMはLLMSの代替品ではありませんが、精度、速度、費用対効果が重要な場合に理想的です。 テクノロジーは、より少ないリソースでより多くを達成するのに役立ちます。それは常にドライバーではなく、プロモーターでした。蒸気エンジンの時代からインターネットバブル時代まで、テクノロジーの力は、問題の解決に役立つ範囲にあります。人工知能(AI)および最近では生成AIも例外ではありません
 コンピュータービジョンタスクにGoogle Geminiモデルを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:26 AM
コンピュータービジョンタスクにGoogle Geminiモデルを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:26 AMコンピュータービジョンのためのGoogleGeminiの力を活用:包括的なガイド 大手AIチャットボットであるGoogle Geminiは、その機能を会話を超えて拡張して、強力なコンピュータービジョン機能を網羅しています。 このガイドの利用方法については、
 Gemini 2.0 Flash vs O4-Mini:GoogleはOpenaiよりもうまくやることができますか?Apr 27, 2025 am 09:20 AM
Gemini 2.0 Flash vs O4-Mini:GoogleはOpenaiよりもうまくやることができますか?Apr 27, 2025 am 09:20 AM2025年のAIランドスケープは、GoogleのGemini 2.0 FlashとOpenaiのO4-Miniの到着とともに感動的です。 数週間離れたこれらの最先端のモデルは、同等の高度な機能と印象的なベンチマークスコアを誇っています。この詳細な比較


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

MantisBT
Mantis は、製品の欠陥追跡を支援するために設計された、導入が簡単な Web ベースの欠陥追跡ツールです。 PHP、MySQL、Web サーバーが必要です。デモおよびホスティング サービスをチェックしてください。

AtomエディタMac版ダウンロード
最も人気のあるオープンソースエディター

VSCode Windows 64 ビットのダウンロード
Microsoft によって発売された無料で強力な IDE エディター

メモ帳++7.3.1
使いやすく無料のコードエディター

EditPlus 中国語クラック版
サイズが小さく、構文の強調表示、コード プロンプト機能はサポートされていません

ホットトピック
 7771
7771 15
15 1644
1644 14
14 1399
1399 52
52 1296
1296 25
25 1234
1234 29
29


