ホームページ >ウェブフロントエンド >jsチュートリアル >javascript_javascript スキルにおける 8 つの主要な並べ替えの実装に関する簡単な説明
javascript_javascript スキルにおける 8 つの主要な並べ替えの実装に関する簡単な説明
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBオリジナル
- 2016-05-16 16:02:111107ブラウズ
新学期が始まって 1 か月、私は筆記試験でデータ構造アルゴリズムの問題が出題される夢を何度も見ました。私はどんな「幽霊」よりもデータ構造を恐れています。はは、「悪夢」が現実になるのを防ぐには、一般的に使用されているデータ構造を見直すことが本当に必要なようです。
データ構造などのプログラミングの基本の重要性は言うまでもありませんが、早速本題に入りましょう。
ソートアルゴリズムは内部ソートと外部ソートに分かれています。内部ソートではメモリが使用されるため、ここでは内部ソートについてのみ説明します。
1. 挿入ソート: 直接挿入ソートとヒルソート
2. 選択ソート: 単純な選択ソートとヒープソート
3. 交換ソート: バブル ソートとクイック ソート
4、マージソート
5、基数ソート

直接挿入ソート
基本的な考え方: 並べ替える一連の数値において、前の (n-1) [n>=2] 個の数値がすでに順序どおりであると仮定すると、最初に n 番目の数値を前の順序の数値に挿入します。これらの n 個の数値もソートされていることがわかります。すべてが整うまでこのサイクルを繰り返します。
ヒルソート
基本的な考え方: アルゴリズムはまず、ソート対象の数値のセットを特定の増分 d (n/2、n はソート対象の数値) に従っていくつかのグループに分割し、各グループに記録されている添字は d だけ異なります。 。各グループ内のすべての要素に対して直接挿入ソートを実行し、次にそれらをより小さい増分 (d/2) でグループ化し、各グループに対して直接挿入ソートを実行します。増分が 1 になると、直接挿入ソート後にソートが完了します。
簡易選択ソート
基本的な考え方: 並べ替える数値のセットから最小の数値を選択し、最初の位置の数値と交換し、残りの数値の中から最も小さい数値を見つけて 2 番目の位置の数値と交換します。 , ので、最後から 2 番目の番号と最後の番号まで haha を見つけます。
ヒープソート
基本的な考え方: ヒープ ソートはツリー選択ソートであり、直接選択ソートを効果的に改良したものです。
(hi>=h2i,hi>=2i 1) または (hi<=h2i,hi<=2i 1 ) の場合に限り、n 個の要素を持つシーケンス (h1, h2,...,hn) ( i=1,2,...,n/2) はヒープと呼ばれます。ここでは、前者の条件を満たすヒープのみを説明します。ヒープの定義から、ヒープの最上位要素 (つまり、最初の要素) が最大の項目 (ビッグトップ ヒープ) でなければならないことがわかります。完全なバイナリ ツリーは、ヒープの構造を非常に直感的に表現できます。ヒープの最上位はルートであり、その他は左のサブツリーと右のサブツリーです。ソート対象の数値列を最初は二分木として順次格納し、そのときヒープのルートノード数が最大となるように格納順序を調整する。次に、ルート ノードをヒープの最後のノードと交換します。次に、以前の (n-1) 個の数値を再調整してヒープを形成します。以下同様に、ノードが 2 つだけのヒープが存在し、それらが交換され、最終的には n 個のノードの順序付けられたシーケンスが取得されます。アルゴリズムの説明から、ヒープのソートには 2 つのプロセスが必要です。1 つはヒープを確立することで、もう 1 つはヒープの先頭とヒープの最後の要素の間の位置を交換することです。したがって、ヒープソートは 2 つの関数で構成されます。 1 つはヒープを構築するペネトレーション関数、もう 1 つはペネトレーション関数を繰り返し呼び出してソートを実現する関数です。
バブルソート
基本的な考え方: 並べ替える一連の数値において、まだ並べ替えられていない範囲内のすべての数値について、隣接する 2 つの数値を上から下に順番に比較して調整します。そして小さいものは上昇します。つまり、2 つの隣接する数値を比較し、それらの順序が順序要件と逆であることが判明した場合は常に、それらの数値が交換されます。
クイックソート
基本的な考え方: ベンチマーク要素 (通常は最初の要素または最後の要素) を選択し、1 回のスキャンで並べ替えるシーケンスを 2 つの部分に分割します。1 つの部分はベンチマーク要素より小さく、もう 1 つの部分はベンチマーク要素より大きくなります。このとき、ベンチマーク要素は正しいソート位置にあり、分割された 2 つの部分が同じ方法で再帰的にソートされます。
並べ替えを結合
基本的なソート: マージソート方法は、2 つ (またはそれ以上) の順序付きリストを新しい順序付きリストにマージすることです。つまり、ソートされるシーケンスはいくつかのサブシーケンスに分割され、各サブシーケンスは連続しています。次に、順序付けられたサブシーケンスを順序付けられたシーケンス全体にマージします。
基数ソート
基本的な考え方: 比較するすべての値(正の整数)を同じ桁長に統一し、桁数が短い数値の前にゼロを追加します。次に、下位ビットから順に 1 つずつ並べ替えます。このようにして、最下位ビットから最上位ビットまでソートした後、シーケンスは順序付けられたシーケンスになります。
コードデモのアドレス: http://lovermap.sinaapp.com/test/sort.html
ここで、8 つの並べ替えアルゴリズムの安定性を分析します。
(ネチズンは、以前のソートの基本的な考え方を組み合わせてソートの安定性を理解するように求められます (8 種類のソートの基本的な考え方は以前に述べたのでここでは繰り返しません)。そうしないと、少し曖昧になる可能性があります)
(1) 直接挿入ソート : 一般的な挿入ソートでは、順序付けされたシーケンスの最後の要素から比較が開始され、それより大きい場合はその直後に挿入され、それ以外の場合はそのまま保持されます。前向きに比較します。挿入された要素と等しい要素が見つかった場合は、等しい要素の後に挿入されます。挿入ソートは安定しています。
(2) ヒル ソート : ヒル ソートは、異なる同期長に応じた要素の挿入ソートです。挿入ソートは安定しており、同じ要素の相対的な順序は変更されませんが、異なる期間で行われます。挿入ソート処理では、同じ要素がそれぞれの挿入ソートで移動する可能性があり、安定性が損なわれるため、ヒル ソートは不安定になります。
(3) 単純な選択ソート : 1 つの選択において、現在の要素が要素より小さく、その小さな要素が現在の要素と等しい要素の後ろにある場合、その後は安定します。交換セックスは破壊されます。言うだけでは少しあいまいかもしれません。小さな例を見てみましょう。858410、最初のスキャンでは、最初の要素 8 が 4 に交換され、元のシーケンス内の 2 つの 8 の相対順序が一致しません。元のシーケンスなので、選択範囲の並べ替えはできません。
(4) ヒープソート : ヒープソートのプロセスは、n/2 番目とその子ノードから開始して最大 (ビッグトップヒープ) または最小 (スモールトップヒープ) を選択します。 3 つの値の合計。この 3 つの要素を選択しても、安定性が損なわれることはありません。ただし、親ノード n/2-1、n/2-2、... の要素を選択する場合、n/2 番目の親ノードが次の要素を交換し、n/2-1 番目の親ノードが次の要素を交換しない可能性があります。最後に同じ要素を交換するため、ヒープのソートが安定しません。
(5) バブルソート : 前の内容からわかるように、バブルソートは 2 つの隣接する要素の比較であり、2 つの要素が等しい場合、これら 2 つの要素の間で交換も行われます。交換する必要はありません。したがってバブルソートは安定しています。
(6) クイックソート : 中心要素がシーケンス内の要素と交換されると、前の要素の安定性が損なわれる可能性が非常に高くなります。小さな例を見てみましょう: 6 4 4 5 4 7 8 9. 最初のソート パスでは、中央の要素 6 と 3 番目の 4 の交換により要素 4 の元のシーケンスが破壊されるため、クイック ソートは不安定になります。
(7) マージソート : 分解されたサブカラムにおいて、要素が 1 つまたは 2 つの場合、1 つの要素は交換されず、2 つの要素はサイズが等しい場合は交換されません。 。シーケンスのマージ プロセス中に、現在の 2 つの要素が等しい場合、結果のシーケンスの前に前のシーケンスの要素が保存されるため、マージ ソートも安定します。
(8) 基数ソート : 最初に低位でソートし、次に上位でソートしてから、最高位までソートします。一部の属性には優先順位が設定されている場合があります。最初に優先順位が低い順に並べ替えられ、次に優先順位が高い順に並べ替えられ、優先順位が同じであるものが最初になります。基数ソートは分別ソートと分別収集に基づいているため、安定しています。
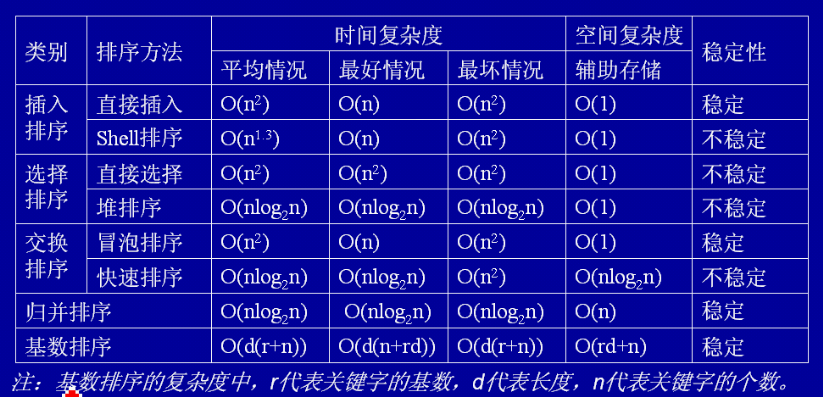
8 種類のソートの分類、安定性、時間計算量、空間計算量の概要:
以上がこの記事の全内容です。皆さんに気に入っていただければ幸いです。

