ホームページ >テクノロジー周辺機器 >AI >トランスフォーマーはカンスフォーマーになりたいですか? MLPが挑戦者KANを迎えるまでに数十年かかった
トランスフォーマーはカンスフォーマーになりたいですか? MLPが挑戦者KANを迎えるまでに数十年かかった
- 王林転載
- 2024-05-03 13:01:04975ブラウズ
MLP (多層パーセプトロン) は何十年も使用されてきましたが、本当に他に選択肢はないのでしょうか?
完全接続フィードフォワードニューラル ネットワークとも呼ばれる多層パーセプトロン (MLP) は、今日の深層学習モデルの基本的な構成要素です。
MLP は機械学習で非線形関数を近似するためのデフォルトの方法であるため、MLP の重要性はいくら強調してもしすぎることはありません。
しかし、MLP は私たちが構築できる最良の非線形回帰変数なのでしょうか? MLP は広く使用されていますが、重大な欠点があります。たとえば、Transformer モデルでは、MLP はほぼすべての非埋め込みパラメーターを消費するため、一般に、後処理分析ツールがないとアテンション レイヤーに比べて解釈しにくくなります。
それでは、MLP に代わるものはあるのでしょうか?
今日はKANさんが登場しました。

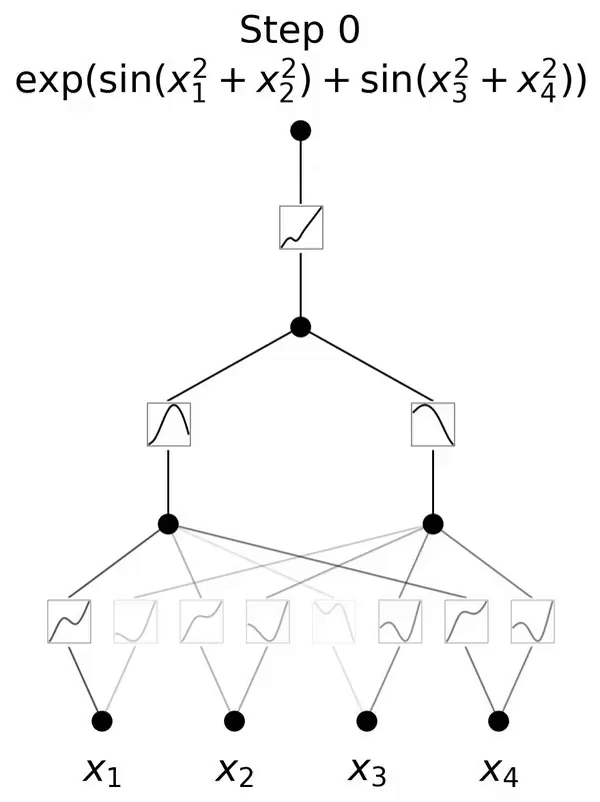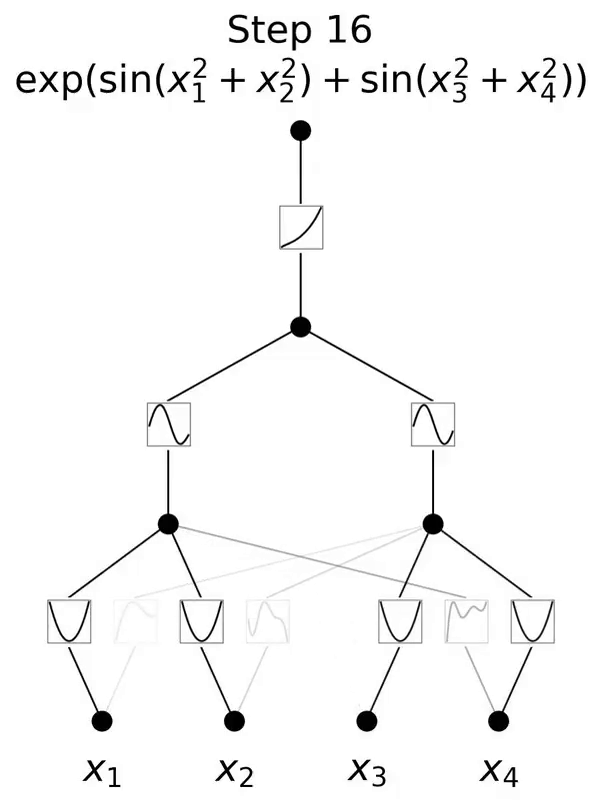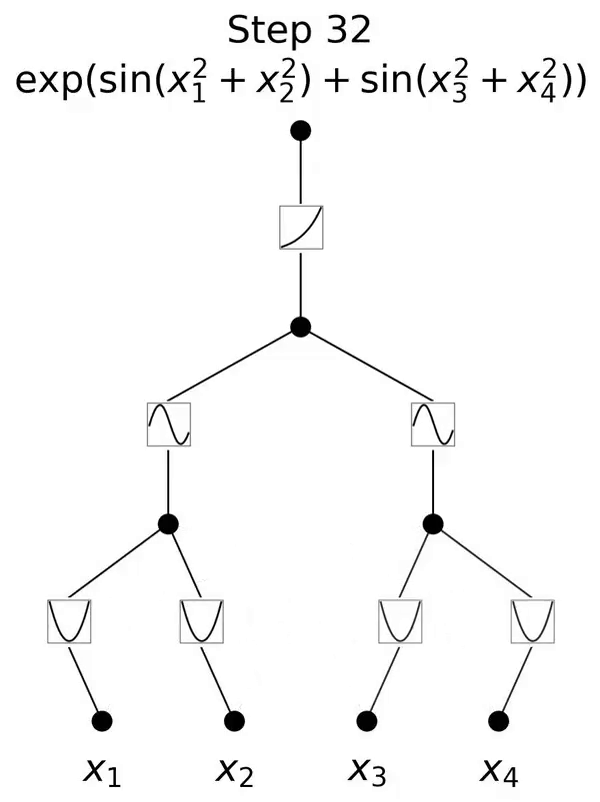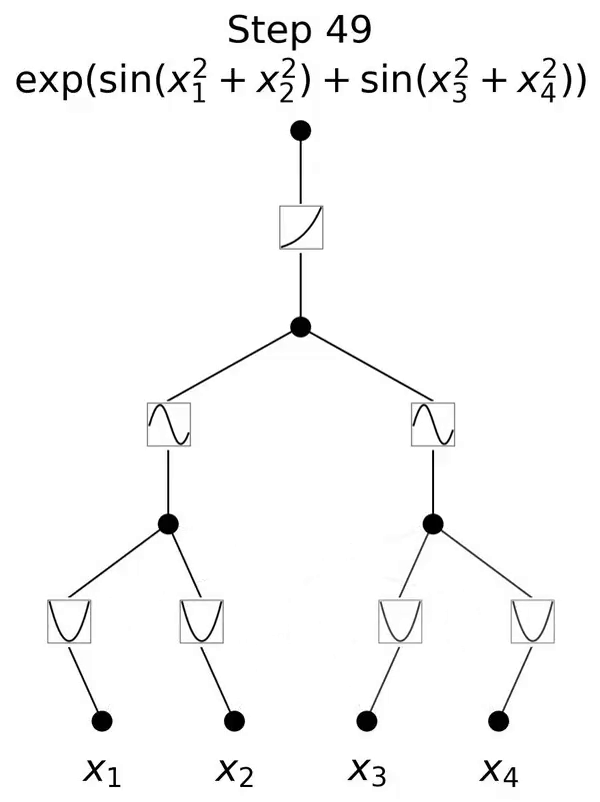

これは、コルモゴロフ-アーノルド表現定理に触発されたネットワークです。
リンク: https://arxiv.org/pdf/2404.19756
Github: https://github.com/KindXiaoming/pykan
この研究が発表されると、海外のソーシャルプラットフォームで幅広い注目と議論を集めました。
一部のネチズンは、コルモゴロフ氏はルーマーハート、ヒントン、ウィリアム氏の1986年の論文よりもはるかに早い1957年には多層ニューラルネットワークを発見したが、コルモゴロフ氏は西側諸国から無視されたと述べた。

# 一部のネチズンは、この論文の発表はディープラーニングの終焉を意味するとも言いました。

一部のネチズンは、この研究がトランスフォーマーの論文と同じくらい破壊的なものになるかどうか疑問に思っています。

しかし、一部の著者は、2018年から2019年にかけて改良されたコルモグロフ・ガボール手法に基づいて同じことを行ったと述べています。
次に、この論文の内容を見てみましょう。
論文の概要
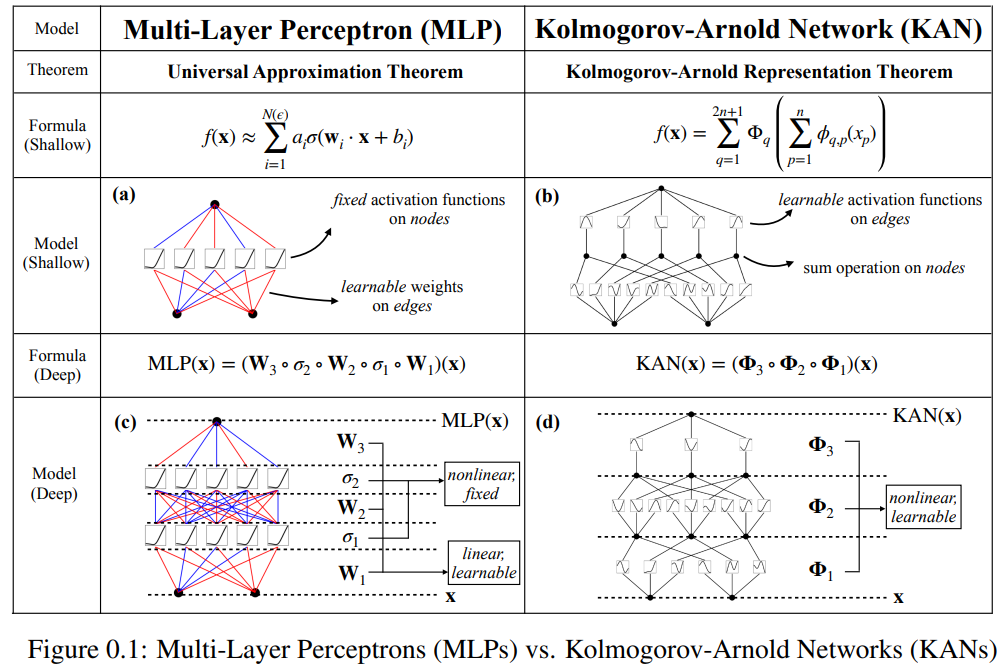
この論文では、コルモゴロフ-アーノルド ネットワーク (KAN) と呼ばれる、多層パーセプトロン (MLP) の有望な代替手段を提案します。 MLP の設計は普遍近似定理からインスピレーションを受けており、KAN の設計はコルモゴロフ-アーノルド表現定理からインスピレーションを得ています。 MLP と同様に、KAN は完全に接続された構造を持っています。図 0.1 に示すように、MLP が固定活性化関数をノード (ニューロン) に配置するのに対し、KAN は学習可能な活性化関数をエッジ (重み) に配置します。したがって、KAN には線形重み行列がまったくありません。各重みパラメータは、スプラインとしてパラメータ化された学習可能な 1 次元関数に置き換えられます。 KAN のノードは、非線形変換を適用せずに、受信信号を単純に合計します。
各 MLP の重みパラメータが KAN のスプライン関数になるため、KAN のコストが高すぎるのではないかと心配する人もいるかもしれません。ただし、KAN では、MLP よりもはるかに小さな計算グラフが可能です。たとえば、研究者らは、PED ソリューションである幅 10 の 2 層の KAN は、幅 100 の 4 層の MLP よりも 100 倍正確であることを示しました (MSE はそれぞれ 10^-7 と 10^-5)。パラメータ効率が 100 倍向上しました (パラメータの数はそれぞれ 10^2 と 10^4)。
コルモゴロフ-アーノルド表現定理を使用してニューラル ネットワークを構築する可能性が研究されています。ただし、ほとんどの作業は元の深さ 2、幅 (2n 1) の表現にこだわっており、ネットワークをトレーニングするためにより現代的な技術 (バックプロパゲーションなど) を活用する機会がありません。この記事の貢献は、元のコルモゴロフ-アーノルド表現を任意の幅と深さに一般化して、今日の深層学習分野で活性化させるとともに、多数の実証実験を使用して「AI 科学」の基本モデルとしての潜在的な役割を強調することです。これは KAN の正確性と解釈可能性によるものです。
KAN は優れた数学的説明機能を備えていますが、実際にはスプラインと MLP を組み合わせたもので、両方の利点を活かし、欠点を回避しています。スプラインは低次元関数での精度が高く、ローカルでの調整が容易で、異なる解像度を切り替えることができます。ただし、スプラインは組み合わせ構造を利用できないため、深刻な COD 問題に悩まされます。一方、MLP は特徴学習機能があるため COD の影響はあまり受けませんが、一変量関数を最適化できないため、低次元空間のスプラインほど正確ではありません。
関数を正確に学習するには、モデルが組み合わせ構造 (外部自由度) を学習するだけでなく、一変量関数 (内部自由度) をよく近似する必要があります。 KAN は、外部的には MLP に似ており、内部的にはスプラインに似ているため、このようなモデルになります。その結果、KAN は (MLP との外部類似性のおかげで) 特徴を学習できるだけでなく、(スプラインとの内部類似性のおかげで) これらの学習された特徴を非常に高い精度で最適化することもできます。
たとえば、高次元関数の場合:
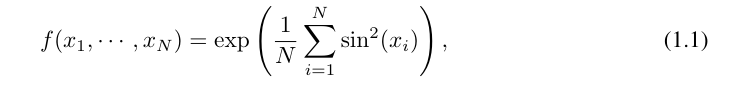
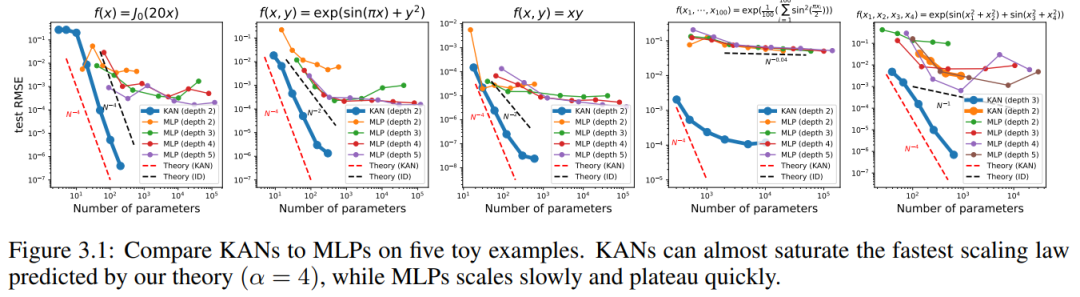
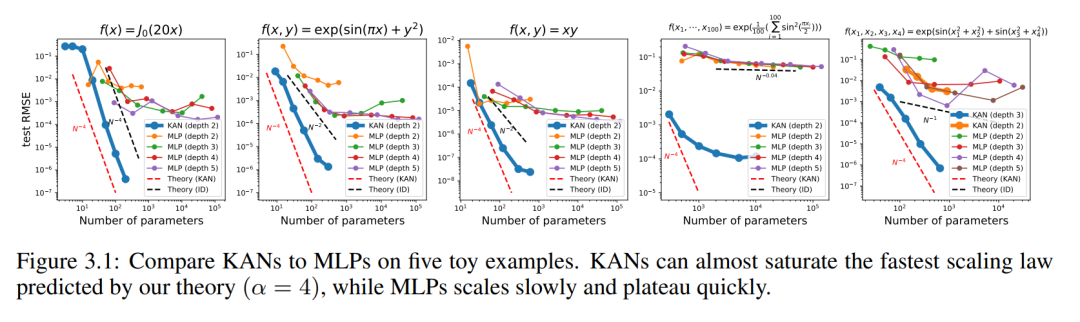
#N が大きい場合、スプラインは COD によって失敗する可能性があります。 MLP は一般化された加法構造を学習しますが、ReLU などの活性化関数を使用して指数関数や正弦関数を近似するのは非常に非効率です。対照的に、KAN は組み合わせ構造と一変量関数を非常によく学習できるため、MLP を大幅に上回ります (図 3.1 を参照)。
この論文では、研究者らは、精度と解釈可能性の点で KAN による MLP の大幅な改善を反映する多数の実験値を示しました。論文の構造を以下の図 2.1 に示します。コードは https://github.com/KindXiaoming/pykan で入手でき、pip install pykan 経由でインストールすることもできます。
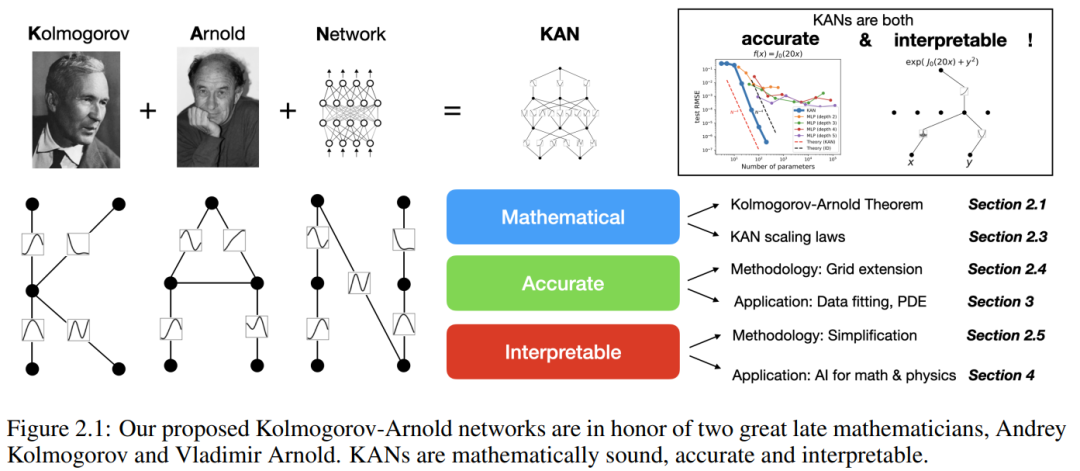
#コルモゴロフ-アーノルド ネットワーク (KAN)
コルモゴロフ-アーノルド表現定理
Vladimir Arnold と Andrey Kolmogorov は、 f が有界領域上の多変数連続関数である場合、 f は単変数連続関数と 2 項加算演算の有限の組み合わせとして記述できることを証明しました。より具体的には、滑らかな関数 f : [0, 1]^n → R の場合、次のように表すことができます。where 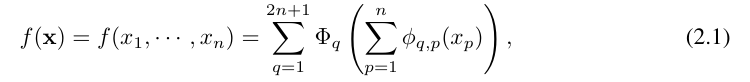 および
および 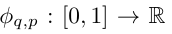
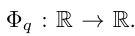
KAN アーキテクチャ
入力と出力のペア {x_i, y_i} で構成される教師あり学習タスクがあるとします。研究者は、すべてのデータ点について y_i ≈ f (x_i) となる関数 f を見つけたいと考えています。式 (2.1) は、適切な単一変数関数 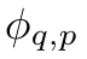 および
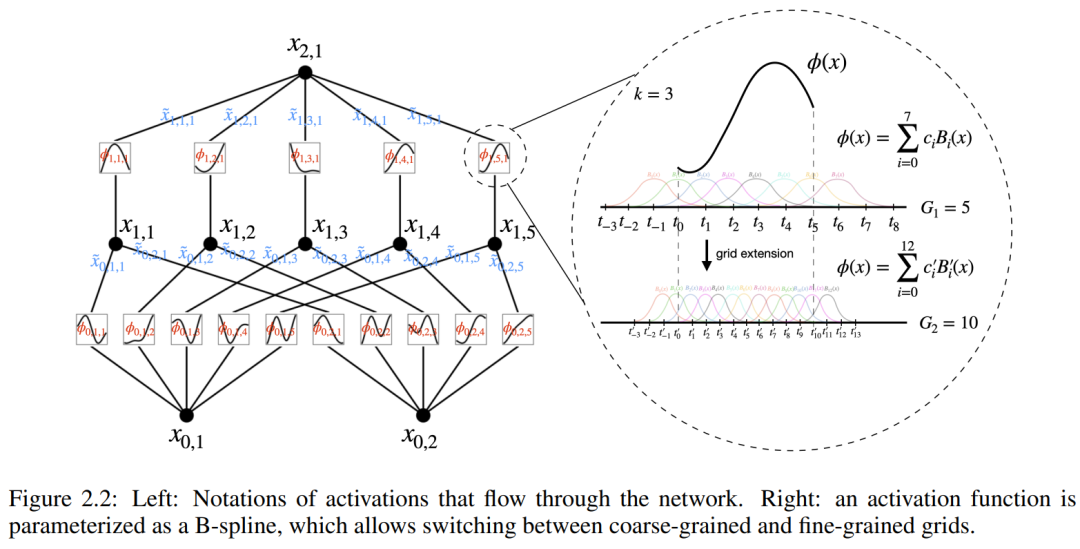
および 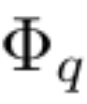 が見つかると、タスクが完了することを意味します。これにより、研究者は式 (2.1) を明示的にパラメータ化するニューラル ネットワークを設計するようになりました。学習する関数はすべて一変量関数であるため、研究者は各一次元関数を、局所的な B スプライン基底関数の学習可能な係数を持つ B スプライン曲線としてパラメーター化します (図 2.2 の右側を参照)。これで、KAN のプロトタイプが完成しました。その計算グラフは式 (2.1) で完全に指定され、図 0.1(b) (入力次元 n = 2) に示されています。これは、活性化関数が配置された 2 層ニューラル ネットワークのように見えます。ノードの代わりにエッジ (ノード上で単純な合計が実行されます)、中間層の幅は 2n 1 です。
が見つかると、タスクが完了することを意味します。これにより、研究者は式 (2.1) を明示的にパラメータ化するニューラル ネットワークを設計するようになりました。学習する関数はすべて一変量関数であるため、研究者は各一次元関数を、局所的な B スプライン基底関数の学習可能な係数を持つ B スプライン曲線としてパラメーター化します (図 2.2 の右側を参照)。これで、KAN のプロトタイプが完成しました。その計算グラフは式 (2.1) で完全に指定され、図 0.1(b) (入力次元 n = 2) に示されています。これは、活性化関数が配置された 2 層ニューラル ネットワークのように見えます。ノードの代わりにエッジ (ノード上で単純な合計が実行されます)、中間層の幅は 2n 1 です。
前述したように、実際には、このようなネットワークは単純すぎるため、任意の精度で任意の関数を平滑化スプラインで近似することはできないと考えられています。したがって、研究者は KAN をより広範囲でより深いネットワークに一般化します。コルモゴロフ-アーノルド表現は 2 層の KAN に対応するため、KAN をより深くする方法は明らかではありません。
画期的な点は、研究者たちが MLP と KAN の類似性に気づいたことです。 MLP では、レイヤー (線形変換と非線形性で構成される) が定義されると、さらに多くのレイヤーを積み重ねてネットワークを深くすることができます。深い KAN を構築するには、まず「KAN 層とは何ですか?」に答える必要があります。研究者らは、n_in 次元の入力と n_out 次元の出力を持つ KAN 層は 1 次元の関数行列として定義できることを発見しました。
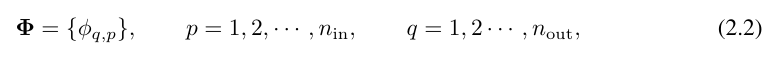
関数  には、以下で説明するトレーニング可能なパラメーターがあります。コルモゴロフ・アーノルドの定理では、内側の関数は n_in = n および n_out = 2n 1 の KAN 層を形成し、外側の関数は n_in = 2n 1 および n_out = 1 の KAN 層を形成します。したがって、式 (2.1) の Kolmogorov-Arnold 表現は、2 つの KAN 層を単純に組み合わせたものになります。さて、コルモゴロフ-アーノルド表現をより深くするということは、単に KAN 層をさらに積み重ねることを意味します。
には、以下で説明するトレーニング可能なパラメーターがあります。コルモゴロフ・アーノルドの定理では、内側の関数は n_in = n および n_out = 2n 1 の KAN 層を形成し、外側の関数は n_in = 2n 1 および n_out = 1 の KAN 層を形成します。したがって、式 (2.1) の Kolmogorov-Arnold 表現は、2 つの KAN 層を単純に組み合わせたものになります。さて、コルモゴロフ-アーノルド表現をより深くするということは、単に KAN 層をさらに積み重ねることを意味します。
さらに理解するには、いくつかの記号の導入が必要です。具体的な例と直感的な理解については、図 2.2 (左) を参照してください。 KAN の形状は整数配列で表されます:

# ここで、n_i は計算グラフの i 番目の層のノードの数です。ここで、(l,i)は第l層のi番目のニューロンを表し、x_l,iは(l,i)のニューロンの活性化値を表す。 l 番目の層と l 番目の層の間には、n_l*n_l 1 個の活性化関数があります。(l, j) と (l 1, i) を結ぶ活性化関数は
 と表されます。
と表されます。
関数 ϕ_l,i,j の起動前の値は単に x_l,i として表され、ϕ_l,i,j の起動後の値は 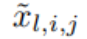 ≡ ϕ_l,i,j (x_l,私)。 (l 1, j) ニューロンの活性化値は、入力されるすべての活性化値の合計です:
≡ ϕ_l,i,j (x_l,私)。 (l 1, j) ニューロンの活性化値は、入力されるすべての活性化値の合計です:
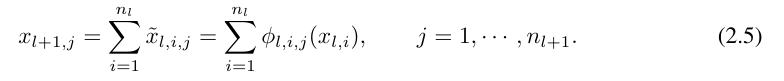
 ##ここで、Φ_l は l 番目の KAN 層に対応する関数行列です。一般的な KAN ネットワークは L 層の組み合わせです。入力ベクトル x_0 ∈ R^n0 が与えられると、KAN の出力は
##ここで、Φ_l は l 番目の KAN 層に対応する関数行列です。一般的な KAN ネットワークは L 層の組み合わせです。入力ベクトル x_0 ∈ R^n0 が与えられると、KAN の出力は
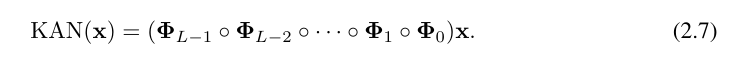 になります。上記の方程式は次のように書くこともできます。方程式 (2.1) の状況を出力次元 n_L = 1 と仮定し、f (x) ≡ KAN (x) を定義します。
になります。上記の方程式は次のように書くこともできます。方程式 (2.1) の状況を出力次元 n_L = 1 と仮定し、f (x) ≡ KAN (x) を定義します。
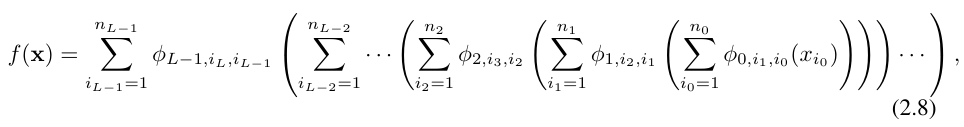
これを書くのは非常に面倒です。対照的に、研究者による KAN 層の抽象化とその視覚化は、より簡潔で直感的です。元の Kolmogorov-Arnold 表現 (2.1) は、形状 [n, 2n 1, 1] の 2 層 KAN に対応します。すべての演算は微分可能であるため、KAN はバックプロパゲーションでトレーニングできることに注意してください。比較のために、MLP はアフィン変換 W と非線形 σ を織り交ぜたものとして書くことができます。
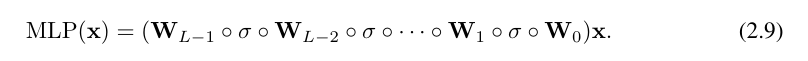
MLP が線形変換と非線形をそれぞれ W と σ として処理することは明らかです。 KAN ではこれらをまとめて Φ として処理します。図 0.1 (c) と (d) では、研究者らは 3 層 MLP と 3 層 KAN を示し、それらの違いを示しています。
KAN の精度
論文の中で、著者らは、さまざまなタスク (回帰および偏微分方程式の解法) において、関数を表現するのに KAN が MLP よりも優れていることも実証しました。より効率的です。また、KAN は壊滅的な忘れを起こすことなく、継続的な学習において自然に機能できることも示しています。
toy Dataset
KAN と MLP のテスト RMSE をパラメータ数の関数として図 3.1 にプロットします。これは、KAN が MLP 曲線よりも適切にスケーリングすることを示しています。特に高次元の例では。比較のために、著者らは、KAN 理論に従って予測された線を赤い破線 (α = k 1 = 4) としてプロットし、Sharma & Kaplan [17] に従って予測された線を黒の破線 (α = k 1 = 4) としてプロットしています。 (k 1)/d = 4/d)。 KAN はより急な赤い線をほぼ埋めることができますが、MLP はより遅い黒い線の速度で収束するのにさえ苦労し、すぐにプラトーに達します。著者らはまた、最後の例では、2 層 KAN のパフォーマンスが 3 層 KAN (形状 [4, 2, 2, 1]) よりもはるかに悪いことに注意しています。これは、深い KAN がより表現力豊かであることを強調しており、同じことが MLP にも当てはまります。つまり、深い MLP は浅い MLP よりも表現力が高いのです。
特別な機能
このパートでは次の 2 つのポイントを示します。
(1) 特別な機能を見つける関数の (ほぼ) コンパクトな KA 表現が可能であり、コルモゴロフ-アーノルド表現の観点から特殊関数の新しい数学的性質を明らかにします。
(2) KAN は、特殊関数を表現する際に MLP よりも効率的かつ正確です。
各データ セットと各モデル ファミリ (KAN または MLP) について、著者らは、図 3.2 に示すように、パラメーターの数と RMSE 平面上にパレート フロンティアをプロットしました。
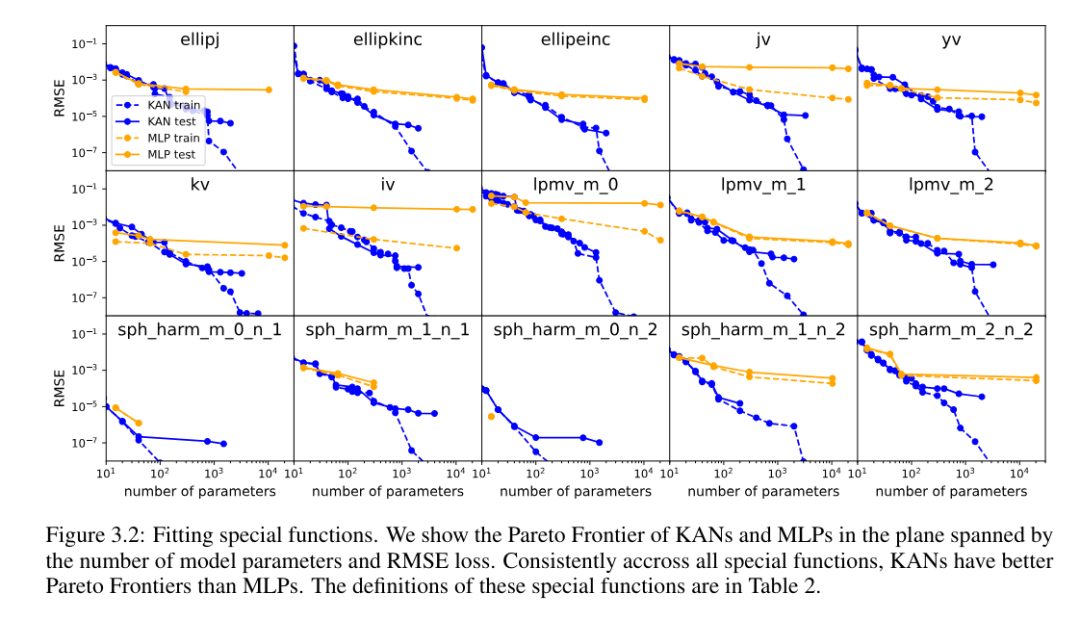
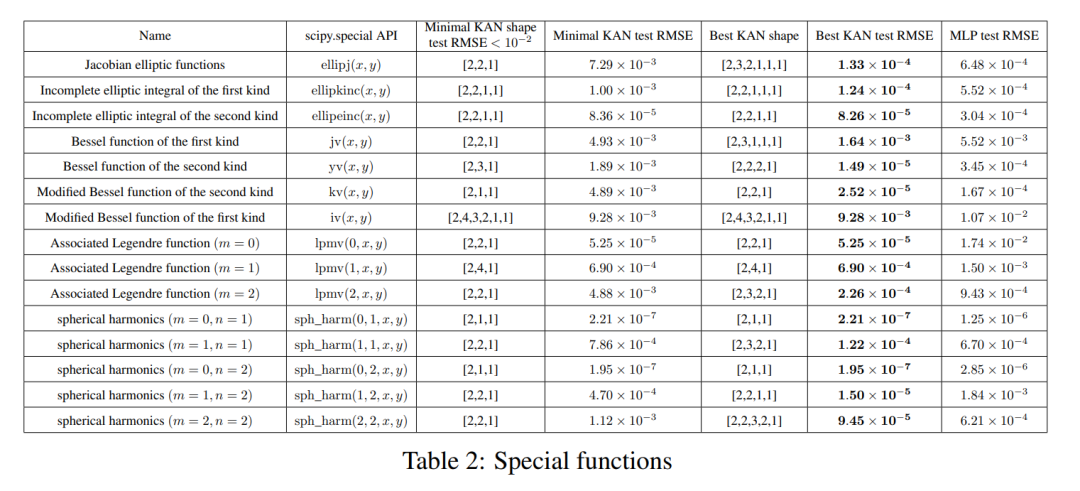
#KAN のパフォーマンスは MLP よりも一貫して優れています。つまり、同じ数のパラメーターを使用すると、KAN は MLP よりも低いトレーニング/テスト損失を達成できます。さらに、著者らは、自動的に発見した特別な機能のための KAN の (驚くほどコンパクトな) 形状を表 2 に報告しています。一方で、これらのコンパクトな表現の意味を数学的に説明するのは興味深いことです。一方、これらのコンパクトな表現は、高次元のルックアップ テーブルをいくつかの 1 次元のルックアップ テーブルに分解できることを意味します。これにより、一部の加算演算を実行する (ほとんど無視できる) オーバーヘッドなしで、大量のメモリを節約できる可能性があります。推論時間。
ファインマン データ セット
前のセクションの設定は、「実際の」KAN 形状が明確にわかっているということです。前のセクションの設定では、「実際の」KAN の形状は明らかにわかりません。このセクションでは中間設定について検討します。データセットの構造を考慮すると、手動で KAN を構築する可能性がありますが、それが最適であるかどうかはわかりません。
各ハイパーパラメータの組み合わせについて、著者は 3 つのランダムなシードを試しました。各データセット (方程式) と各手法について、ランダムなシードと深さでの最良のモデル (最小の KAN 形状または最小のテスト損失) の結果を表 3 に報告しています。
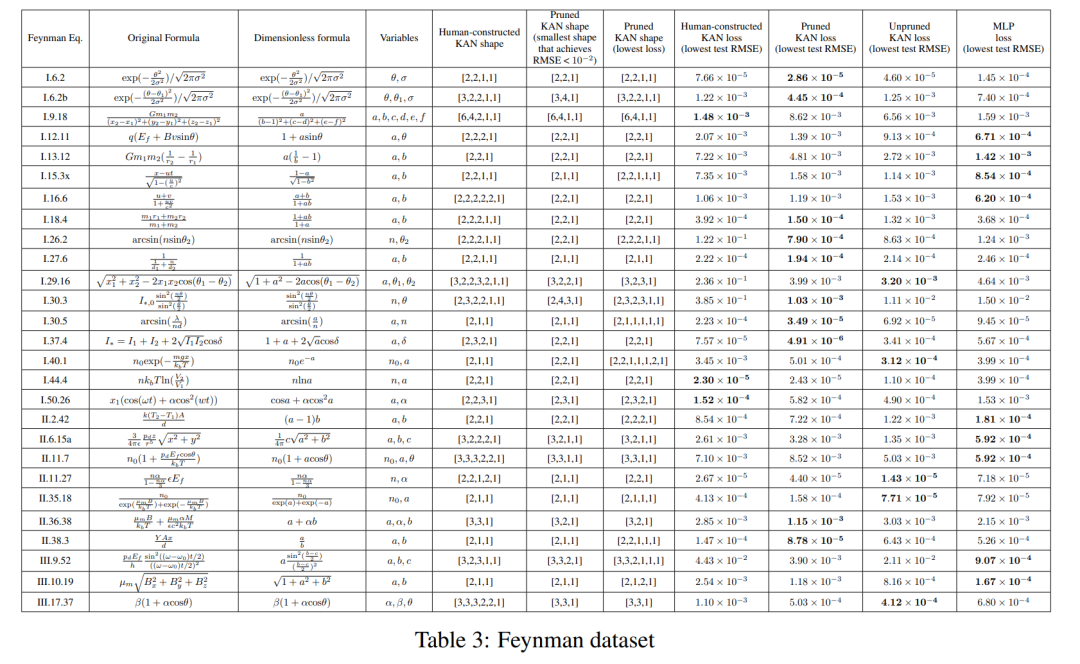
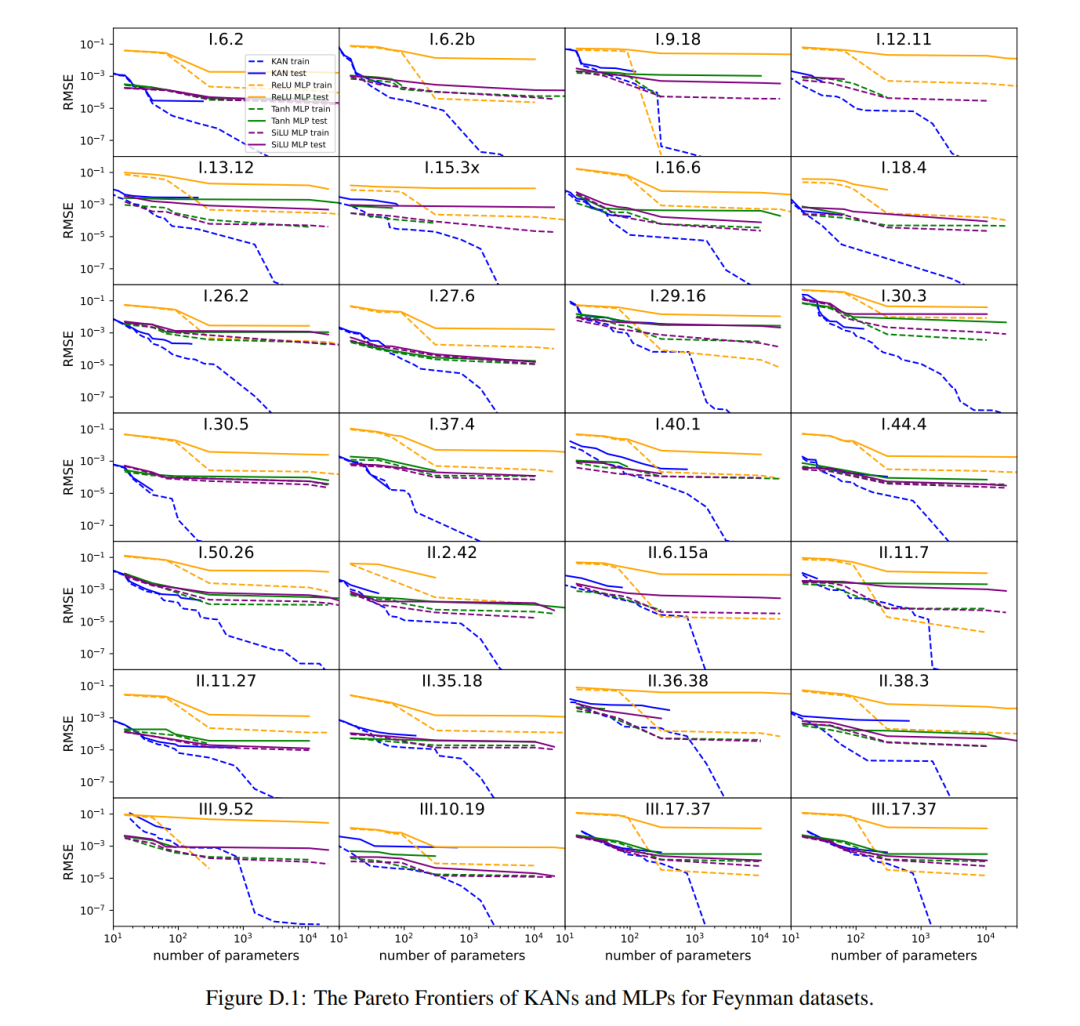
彼らは、MLP と KAN が平均して同等のパフォーマンスを発揮することを発見しました。図 D.1 に示すように、各データセットと各モデル ファミリ (KAN または MLP) について、著者らはパラメーターの数と RMSE 損失によって形成される平面上にパレート フロンティアをプロットしました。彼らは、ファインマンのデータセットが単純すぎて、KAN によるさらなる改善を可能にできないのではないかと推測しています。これは、振動的な動作を示すことが多い特殊関数の複雑さとは対照的に、変数の依存関係が滑らかまたは単調であることが多いためです。
偏微分方程式を解く
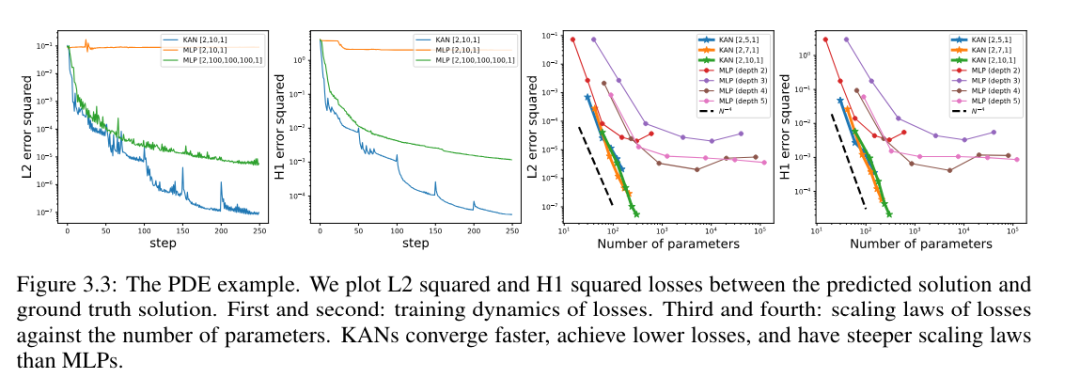
著者らは、同じハイパーパラメータを使用して KAN アーキテクチャと MLP アーキテクチャを比較しました。彼らは、L^2 ノルムとエネルギー (H^1) ノルムの誤差を測定し、より小さなネットワークとより少ないパラメーターを使用しながら、KAN がより優れたスケーリング則とより小さな誤差を達成することを観察しました (図 3.3 を参照)。したがって、彼らは、KAN が偏微分方程式 (PDE) モデル削減のための優れたニューラル ネットワーク表現として機能する可能性があると推測しました。
継続学習
著者らは、KAN には局所的な可塑性があり、スプラインの局所性を利用することで壊滅的な忘却を回避できることを示しています。考え方は簡単です。スプラインの基底がローカルであるため、サンプルは近くのいくつかのスプライン係数にのみ影響し、遠方の係数は変更されません(これが私たちが望むことです。遠方の領域には、保持したい情報がすでに格納されている可能性があるためです)。 。対照的に、MLP は通常、ReLU/Tanh/SiLU などのグローバル アクティベーション関数を使用するため、ローカルな変更が制御不能に遠くの領域に伝播し、そこに保存されている情報が破壊される可能性があります。
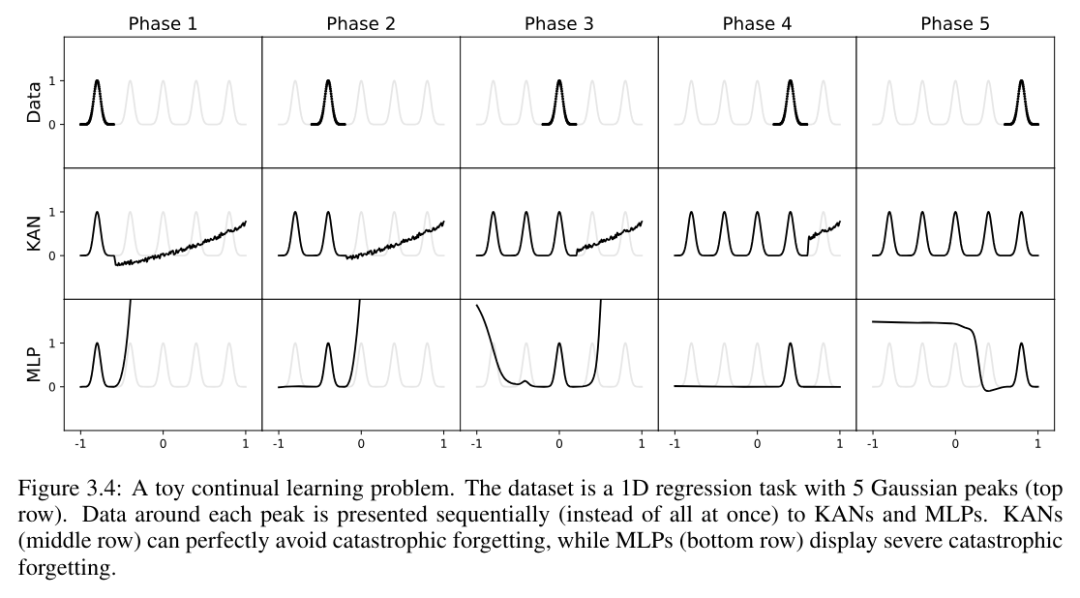
著者は、この直感を検証するために簡単な例を使用しています。 1 次元回帰タスクは 5 つのガウス ピークで構成されます。図 3.4 の上段に示すように、各ピークの周囲のデータは (一度にすべてではなく) 順番に表示され、KAN と MLP に別々に表示されます。各トレーニング段階後の KAN と MLP の予測結果をそれぞれ中段と下段に示します。予想どおり、KAN は現在の段階でデータが存在する領域のみを再構築し、以前の領域は変更されません。対照的に、MLP は新しいデータ サンプルを見た後に領域全体を再構成するため、致命的な忘却につながります。
KAN は解釈可能です
記事の第 4 章で、著者は、解釈可能なテクノロジーにより KAN が解釈可能であることを示しています。そしてインタラクティブ。彼らは、合成タスク (セクション 4.1 および 4.2) だけでなく、実際の科学研究でも KAN の適用をテストしたいと考えていました。彼らは、KAN が接合理論 (セクション 4.3) の複雑な関係と凝縮物性物理学 (セクション 4.4) の相転移境界を (再) 発見できることを示しています。 KAN は、その精度と解釈可能性により、AI サイエンスの基礎モデルとなる可能性があります。
ディスカッション
この論文では、著者は数学的基礎、アルゴリズム、アプリケーションの観点から KAN の限界と将来の開発の方向性について議論しています。
数学的側面: 著者は KAN (定理 2.1) の予備的な数学的分析を実行しましたが、数学的理解はまだ非常に限られています。コルモゴロフ-アーノルドの表現定理は数学的に徹底的に研究されていますが、これは [n, 2n 1, 1] の形状の KAN に対応しており、これは KAN の非常に限定されたサブクラスです。より深い KAN での経験的な成功は、数学的に基礎的な何かを暗示しているのでしょうか?魅力的な一般化されたコルモゴロフ-アーノルド定理は、2 つの層の組み合わせを超えて「より深い」コルモゴロフ-アーノルド表現を定義でき、活性化関数の滑らかさを深さに関連付けることができる可能性があります。元の (深さ 2) コルモゴロフ-アーノルド表現ではスムーズに表現できない関数があるとしますが、深さ 3 以上ではスムーズに表現できるとします。この「コルモゴロフ・アーノルドの深さ」の概念を関数クラスの特徴付けに使用できますか?
アルゴリズムの観点から、彼らは次の点について議論しました:
精度。アーキテクチャの設計とトレーニングには十分に調査されていないオプションが複数あるため、精度をさらに向上させるための代替手段がある可能性があります。たとえば、スプライン活性化関数は、放射基底関数または他のローカル カーネル関数に置き換えられる可能性があります。適応グリッド戦略を使用できます。 ######効率。 KAN が遅い主な理由の 1 つは、異なるアクティベーション関数がバッチ計算 (同じ関数を介して渡される大量のデータ) を利用できないためです。実際、活性化関数をグループ (「複数」) にグループ化し、グループのメンバーが同じ活性化関数を共有することで、MLP (すべての活性化関数が同じ) と KAN (すべての活性化関数が異なる) の間を補間できます。
KAN と MLP のハイブリッド。 MLP と比較すると、KAN には 2 つの主な違いがあります。
- (i) アクティベーション関数はノードではなくエッジにあります。 ii) 活性化関数は固定されるものではなく、学習可能です。
- KAN の利点をよりよく説明する変更はどれですか?著者らは、付録 B で予備的な結果を示しています。そこでは、(ii) を備えたモデル、つまり、活性化関数が学習可能 (KAN のように) であるが、(i) を持たない、つまり、活性化関数がノードに配置されている (MLP のように) モデルを研究しています。 )。さらに、活性化関数が固定されている (MLP など) がエッジに配置されている (KAN など) 別のモデルを構築することもできます。
-
適応性。スプライン基底関数には固有の局所性があるため、KAN の設計とトレーニングに適応性を導入して、精度と効率を向上させることができます。マルチグリッド法やドメイン依存の基底関数などのマルチレベルのトレーニングのアイデアについては、[93、94] を参照してください。 [95] のマルチスケール手法と同様です。
アプリケーション: 著者らは、物理方程式の当てはめや偏微分方程式の解法など、科学関連のタスクでは KAN が MLP よりも効果的であるという予備的な証拠をいくつか提示しました。彼らは、KAN がナビエ・ストークス方程式、密度汎関数理論、または回帰または PDE 解として定式化できるその他のタスクの解決にも有望である可能性があると期待しています。 彼らはまた、機械学習に関連するタスクに KAN を適用することを望んでいます。そのためには、トランスフォーマーなどの現在のアーキテクチャに KAN を統合する必要があります。トランスフォーマー内の MLP を KAN に置き換える「kansformers」を提案できます。
AI サイエンス用の言語モデルとしての KAN: 大規模な言語モデルは、自然言語を使用できるすべての人にとって役立つため、変革をもたらします。科学の言語は関数です。 KAN は解釈可能な関数で構成されているため、人間のユーザーが KAN を見つめていると、関数型言語を使用して KAN と通信しているようなものになります。この段落は、特定のツール KAN ではなく、AI と科学者のコラボレーション パラダイムを強調することを目的としています。人間がコミュニケーションに異なる言語を使用するのと同じように、著者らは、KAN は AI と人間のコミュニケーションを可能にする最初の言語の 1 つになるものの、将来的には KAN が AI 科学の言語の 1 つにすぎなくなると予測しています。 。しかし、KAN の実現のおかげで、AI と科学者のコラボレーション パラダイムはかつてないほど簡単かつ便利になり、AI 科学へのアプローチ方法を再考するようになりました。つまり、AI 科学者が欲しいのか、それとも科学者を支援する AI が欲しいのか、ということです。 (完全に自動化された)AI における科学者にとっての固有の難しさは、人間の好みを数値化して AI の目標に体系化することの難しさです。実際、どの関数が単純であるか、または説明可能であるかについて、異なる分野の科学者は異なる感情を持っている可能性があります。したがって、科学者にとっては、科学の言語 (機能) を話し、特定の科学領域に合わせて個々の科学者の帰納的バイアスと容易に相互作用できる AI を持つことが望ましいです。
重要な質問: KAN または MLP を使用しますか?
現時点での KAN の最大のボトルネックは、トレーニング速度の遅さです。パラメーターの数が同じ場合、KAN のトレーニング時間は通常、MLP の 10 倍になります。著者らは、正直に言うと、KAN の効率を最適化する努力をしていないため、KAN のトレーニング速度の遅さは、根本的な制限というよりも、将来的に改善できるエンジニアリングの問題であると考えていると述べています。モデルをすばやくトレーニングしたい場合は、MLP を使用する必要があります。ただし、他のケースでは、KAN は MLP と同等かそれ以上の性能を発揮するため、試してみる価値があります。図 6.1 のデシジョン ツリーは、KAN をいつ使用するかを決定するのに役立ちます。 つまり、解釈可能性や正確性を重視し、トレーニングの遅さが大きな問題ではない場合、著者は KAN を試してみることを推奨しています。
詳細については、原論文をお読みください。
以上がトランスフォーマーはカンスフォーマーになりたいですか? MLPが挑戦者KANを迎えるまでに数十年かかったの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

