 テクノロジー周辺機器
テクノロジー周辺機器 AI
AI AI4Science の基礎: 幾何学グラフ ニューラル ネットワーク、最も包括的なレビューがここにあります。中国人民大学ヒルハウスはテンセントAIラボ、清華大学、スタンフォード大学などと共同でリリースした。
AI4Science の基礎: 幾何学グラフ ニューラル ネットワーク、最も包括的なレビューがここにあります。中国人民大学ヒルハウスはテンセントAIラボ、清華大学、スタンフォード大学などと共同でリリースした。AI4Science の基礎: 幾何学グラフ ニューラル ネットワーク、最も包括的なレビューがここにあります。中国人民大学ヒルハウスはテンセントAIラボ、清華大学、スタンフォード大学などと共同でリリースした。

編集者 | XS
Nature は、タンパク質合成技術 Chroma と結晶材料設計手法 GNoME という 2 つの重要な研究結果を 2023 年 11 月に発表しました。どちらの研究でも、科学データを処理するツールとしてグラフ ニューラル ネットワークを採用しました。
実際、グラフ ニューラル ネットワーク、特に幾何学的グラフ ニューラル ネットワークは、常に科学知能 (AI for Science) 研究にとって重要なツールです。これは、科学分野における粒子、分子、タンパク質、結晶などの物理システムを特別なデータ構造、つまり幾何学グラフにモデル化できるためです。
一般的なトポロジー図とは異なり、物理システムをより適切に説明するために、幾何学図は不可欠な空間情報を追加し、平行移動、回転、反転の物理的対称性を満たす必要があります。物理システムのモデリングにおける幾何学グラフ ニューラル ネットワークの優位性を考慮して、近年さまざまな手法が登場し、論文数は増え続けています。
最近、中国人民大学とヒルハウスは、テンセント AI ラボ、清華大学、スタンフォード大学、その他の機関と協力して、レビュー論文「幾何学グラフ ニューラル ネットワークの調査: データ構造、モデル」を発表しました。およびアプリケーション"。このレビューでは、群理論や対称性などの理論的知識の簡単な紹介に基づいて、データ構造やモデルから多数の科学的応用に至るまで、関連する幾何学グラフ ニューラル ネットワークの文献を体系的にレビューします。

紙のリンク: https://arxiv.org/abs/2403.00485
GitHub リンク: https:/ /github.com/RUC-GLAD/GGNN4Science
このレビューでは、著者は 300 以上の参考文献を調査し、3 つの異なる幾何学グラフ ニューラル ネットワーク モデルを要約し、粒子指向の関連する合計 23 モデルを紹介しました。分子、タンパク質などのさまざまな科学データに基づいてさまざまなタスクに対応する手法を確立し、50 を超える関連する評価データセットが収集されています。最後に、幾何学グラフの基本モデル、大規模な言語モデルとの組み合わせなど、将来の研究の方向性を展望しています。
以下は各章の簡単な紹介です。
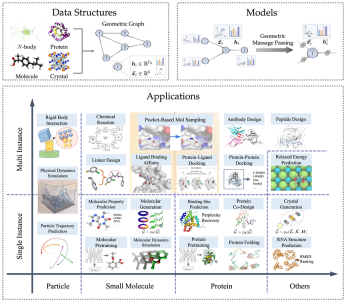
#幾何グラフのデータ構造
幾何グラフは、隣接行列、ノード特性、ノードの幾何情報(座標など)から構成されます。ユークリッド空間では、幾何学的図形は通常、並進、回転、鏡映の物理的対称性を示します。これらの変換を記述するには、通常、ユークリッド群、並進群、直交群、順列群などの群が使用されます。直観的には、移動、平行移動、回転、反転の 4 つの操作を特定の順序で組み合わせたものとして理解できます。 AI for Science の多くの分野にとって、幾何学グラフは、小分子、タンパク質、結晶、物理点群などを含む多くの物理システムを表現するために使用できる強力で汎用性の高い表現方法です。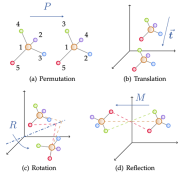
幾何グラフ ニューラル ネットワーク モデル
実際の問題における解決目標の対称性の要件に従って、この記事では幾何学的グラフを使用します。グラフ ニューラル ネットワーク ネットワークは、不変 (不変) モデル、等変 (等変) モデル、Transformer アーキテクチャからインスピレーションを得た Geometric Graph Transformer の 3 つのカテゴリに分類されます。球面調和の高度に制御可能なモデルについて。上記のルールに従って、この記事では、近年よく知られている幾何グラフ ニューラル ネットワーク モデルを収集し、分類します。
高次の制御可能なモデルは、高次の球面調和関数とウィグナー D 行列を使用して、システムの幾何学的情報を表現します。この方法では、量子力学のクレブシュ ゴルダン係数を使用して、既約表現の次数を制御します。幾何学的メッセージパッシングプロセスを実現します。

#幾何グラフ ニューラル ネットワークは、この種の設計によって保証される対称性によって精度が大幅に向上し、生成タスクでも威力を発揮します。
次の図は、QM9、PDBBind の 3 つのデータセットに対する幾何学的グラフ ニューラル ネットワークと従来のモデルを使用した、分子特性予測、タンパク質とリガンドのドッキング、抗体設計 (生成) の 3 つのタスクの結果です。幾何学グラフ ニューラル ネットワークの利点がはっきりとわかります。

科学的応用
科学的応用に関しては、このレビューでは物理学 (粒子)、生化学 (小分子、タンパク質) を取り上げます。結晶などの他のアプリケーション シナリオと同様に、タスク定義と確保するために必要な対称性のタイプから始まり、各タスクで一般的に使用されるデータ セットとこのタイプのタスクでの古典的なモデル設計のアイデアが紹介されます。

上の表は、さまざまな分野における一般的なタスクと古典的なモデルを示しています。その中で、単一のインスタンスと複数のインスタンス (複数の参加が必要な化学反応など) に応じて、分子)、記事は別です。小分子-小分子、小分子-タンパク質、タンパク質-タンパク質の 3 つの領域が区別されます。
現場でのモデル設計と実験開発をより容易にするために、この記事では、単一インスタンスと複数インスタンスに基づいた 2 種類のタスクの共通データ セットとベンチマーク (ベンチマーク) を数え、さまざまなデータのサンプルを記録しています。タスクの量と種類。
次の表は、一般的な単一インスタンス タスクのデータ セットをまとめたものです。


将来の見通し
この記事では、出発点として役立つことを期待して、いくつかの側面について予備的な見通しを示します。 1. 幾何グラフ基本モデルさまざまなタスクや分野で統一された基本モデルを使用する利点は、GPT シリーズ モデルの大幅な進歩に反映されています。このアイデアを幾何学グラフ ニューラル ネットワークの設計に導入するために、タスク空間、データ空間、モデル空間で合理的な設計をどのように実行するかは、依然として興味深い未解決の問題です。
2. モデルのトレーニングと実際の実験検証の効率的なサイクル科学データの取得には費用と時間がかかり、評価は独立したデータセットでのみ行われます。現実世界からのフィードバックを直接反映することはできません。 GNoME (グラフ ネットワークのトレーニング、密度汎関数理論の計算、材料の発見と合成のための自動ラボを含むエンドツーエンドのパイプラインを統合する) と同様の、効率的なモデルと現実の反復実験パラダイムを実現する方法の重要性は、今後ますます高まっていくでしょう。日。
3. 大規模言語モデル (LLM) との統合大規模言語モデル (LLM) には、さまざまな分野をカバーする豊富な知識があることが広く証明されています。分子特性の予測や薬剤設計などの特定のタスクに LLM を利用する研究はいくつかありますが、それらはプリミティブまたは分子グラフ上でのみ機能します。これらを幾何学グラフ ニューラル ネットワークと有機的に組み合わせて、3D 構造情報を処理し、3D 構造の予測や生成を実行できるようにする方法は、依然として非常に困難です。
4. 等分散制約の緩和データ効率とモデルの汎化能力を高めるために等分散が重要であることは間違いありませんが、強すぎることに注意する価値があります。等分散制約はモデルに対して制限が強すぎる場合があり、パフォーマンスに悪影響を与える可能性があります。したがって、設計されたモデルの等分散性と適応性のバランスをどのように取るかは非常に興味深い問題です。この分野の探求は、モデルの動作についての理解を深めるだけでなく、より幅広い適用性を備えた、より堅牢で一般的なソリューションの開発への道を開くことにもなります。
参考文献[1] Schütt K、Kindermans P J、Sauceda Felix H E、他 Schnet: 量子相互作用をモデル化するための連続フィルター畳み込みニューラル ネットワーク[ J ]. 神経情報処理システムの進歩、2017、30.
[2] Satorras V G、Hoogeboom E、Welling M. E (n) 等変グラフ ニューラル ネットワーク[C]//機械学習に関する国際会議。 PMLR、2021: 9323-9332.
[3] Thomas N、Smidt T、Kearnes S、他。テンソル フィールド ネットワーク: 3 次元点群の回転および平行移動等価ニューラル ネットワーク[J]。 arXiv プレプリント arXiv:1802.08219、2018.
[4] Gaseiger J、Groß J、Günnemann S. 分子グラフのための方向性メッセージ パッシング[C]//学習表現に関する国際会議。 2019.
[5] Gaseiger J、Becker F、Günnemann S. Gemnet: 分子のユニバーサル方向グラフ ニューラル ネットワーク[J]。 Advances in Neural Information Processing Systems、2021、34: 6790-6802.
[6] Merchant A、Batzner S、Schoenholz S S、他。材料発見のための深層学習のスケーリング[J]。自然、2023、624(7990): 80-85.
以上がAI4Science の基礎: 幾何学グラフ ニューラル ネットワーク、最も包括的なレビューがここにあります。中国人民大学ヒルハウスはテンセントAIラボ、清華大学、スタンフォード大学などと共同でリリースした。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 踊りましょう:私たちの人間のニューラルネットを微調整するための構造化された動きApr 27, 2025 am 11:09 AM
踊りましょう:私たちの人間のニューラルネットを微調整するための構造化された動きApr 27, 2025 am 11:09 AM科学者は、彼らの機能を理解するために、人間とより単純なニューラルネットワーク(C. elegansのものと同様)を広く研究してきました。 ただし、重要な疑問が生じます。新しいAIと一緒に効果的に作業するために独自のニューラルネットワークをどのように適応させるのか
 新しいGoogleリークは、Gemini AIのサブスクリプションの変更を明らかにしますApr 27, 2025 am 11:08 AM
新しいGoogleリークは、Gemini AIのサブスクリプションの変更を明らかにしますApr 27, 2025 am 11:08 AMGoogleのGemini Advanced:Horizonの新しいサブスクリプションティア 現在、Gemini Advancedにアクセスするには、1か月あたり19.99ドルのGoogle One AIプレミアムプランが必要です。 ただし、Android Authorityのレポートは、今後の変更を示唆しています。 最新のGoogle p
 データ分析の加速がAIの隠されたボトルネックをどのように解決しているかApr 27, 2025 am 11:07 AM
データ分析の加速がAIの隠されたボトルネックをどのように解決しているかApr 27, 2025 am 11:07 AM高度なAI機能を取り巻く誇大宣伝にもかかわらず、エンタープライズAIの展開内に大きな課題が潜んでいます:データ処理ボトルネック。 CEOがAIの進歩を祝う間、エンジニアはクエリの遅い時間、過負荷のパイプライン、
 MarkitDown MCPは、任意のドキュメントをマークダウンに変換できます!Apr 27, 2025 am 09:47 AM
MarkitDown MCPは、任意のドキュメントをマークダウンに変換できます!Apr 27, 2025 am 09:47 AMドキュメントの取り扱いは、AIプロジェクトでファイルを開くだけでなく、カオスを明確に変えることです。 PDF、PowerPoint、Wordなどのドキュメントは、あらゆる形状とサイズでワークフローをフラッシュします。構造化された取得
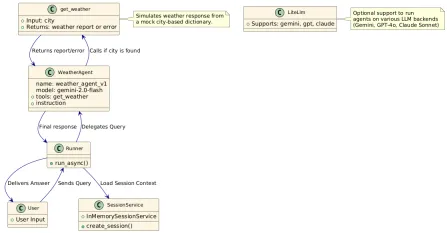 建物のエージェントにGoogle ADKを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:42 AM
建物のエージェントにGoogle ADKを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:42 AMGoogleのエージェント開発キット(ADK)のパワーを活用して、実際の機能を備えたインテリジェントエージェントを作成します。このチュートリアルは、ADKを使用して会話エージェントを構築し、GeminiやGPTなどのさまざまな言語モデルをサポートすることをガイドします。 w
 効果的な問題解決のためにLLMを介したSLMの使用 - 分析VidhyaApr 27, 2025 am 09:27 AM
効果的な問題解決のためにLLMを介したSLMの使用 - 分析VidhyaApr 27, 2025 am 09:27 AMまとめ: Small Language Model(SLM)は、効率のために設計されています。それらは、リソース不足、リアルタイム、プライバシーに敏感な環境の大手言語モデル(LLM)よりも優れています。 特にドメインの特異性、制御可能性、解釈可能性が一般的な知識や創造性よりも重要である場合、フォーカスベースのタスクに最適です。 SLMはLLMSの代替品ではありませんが、精度、速度、費用対効果が重要な場合に理想的です。 テクノロジーは、より少ないリソースでより多くを達成するのに役立ちます。それは常にドライバーではなく、プロモーターでした。蒸気エンジンの時代からインターネットバブル時代まで、テクノロジーの力は、問題の解決に役立つ範囲にあります。人工知能(AI)および最近では生成AIも例外ではありません
 コンピュータービジョンタスクにGoogle Geminiモデルを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:26 AM
コンピュータービジョンタスクにGoogle Geminiモデルを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:26 AMコンピュータービジョンのためのGoogleGeminiの力を活用:包括的なガイド 大手AIチャットボットであるGoogle Geminiは、その機能を会話を超えて拡張して、強力なコンピュータービジョン機能を網羅しています。 このガイドの利用方法については、
 Gemini 2.0 Flash vs O4-Mini:GoogleはOpenaiよりもうまくやることができますか?Apr 27, 2025 am 09:20 AM
Gemini 2.0 Flash vs O4-Mini:GoogleはOpenaiよりもうまくやることができますか?Apr 27, 2025 am 09:20 AM2025年のAIランドスケープは、GoogleのGemini 2.0 FlashとOpenaiのO4-Miniの到着とともに感動的です。 数週間離れたこれらの最先端のモデルは、同等の高度な機能と印象的なベンチマークスコアを誇っています。この詳細な比較


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

Safe Exam Browser
Safe Exam Browser は、オンライン試験を安全に受験するための安全なブラウザ環境です。このソフトウェアは、あらゆるコンピュータを安全なワークステーションに変えます。あらゆるユーティリティへのアクセスを制御し、学生が無許可のリソースを使用するのを防ぎます。

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

mPDF
mPDF は、UTF-8 でエンコードされた HTML から PDF ファイルを生成できる PHP ライブラリです。オリジナルの作者である Ian Back は、Web サイトから「オンザフライ」で PDF ファイルを出力し、さまざまな言語を処理するために mPDF を作成しました。 HTML2FPDF などのオリジナルのスクリプトよりも遅く、Unicode フォントを使用すると生成されるファイルが大きくなりますが、CSS スタイルなどをサポートし、多くの機能強化が施されています。 RTL (アラビア語とヘブライ語) や CJK (中国語、日本語、韓国語) を含むほぼすべての言語をサポートします。ネストされたブロックレベル要素 (P、DIV など) をサポートします。

SublimeText3 中国語版
中国語版、とても使いやすい

AtomエディタMac版ダウンロード
最も人気のあるオープンソースエディター

ホットトピック
 7767
7767 15
15 1644
1644 14
14 1399
1399 52
52 1293
1293 25
25 1234
1234 29
29

