ホームページ >テクノロジー周辺機器 >AI >数行のコードで UNet を安定化! 中山大学などが ScaleLong 普及モデルを提案: Scaling の疑問から Scaling になるまで
数行のコードで UNet を安定化! 中山大学などが ScaleLong 普及モデルを提案: Scaling の疑問から Scaling になるまで
- PHPz転載
- 2024-03-01 10:01:02670ブラウズ
標準的な UNet 構造では、ロング スキップ接続のスケーリング係数 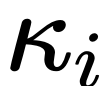 は通常 1 です。
は通常 1 です。
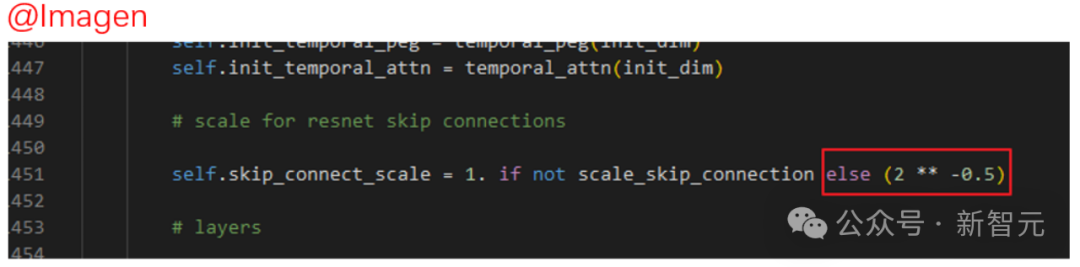
ただし、Imagen、スコアベースの生成モデル、SR3 などの一部のよく知られた拡散モデルの作品では、すべて 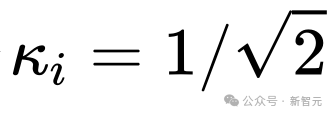 ## が設定されています。 # 、そのような設定により拡散モデルのトレーニングを効果的に加速できることがわかりました。
## が設定されています。 # 、そのような設定により拡散モデルのトレーニングを効果的に加速できることがわかりました。
 質問のスケーリング
質問のスケーリング
まず第一に、この種の経験的な表示では、この設定がどのような役割を果たしているのかがわかりにくくなります。
また、
しか設定できないのか、それとも他の定数を使用できるのかもわかりません。 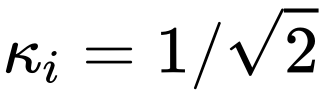
著者はこれについて多くの質問をしています...
写真 理解スケーリング
理解スケーリング
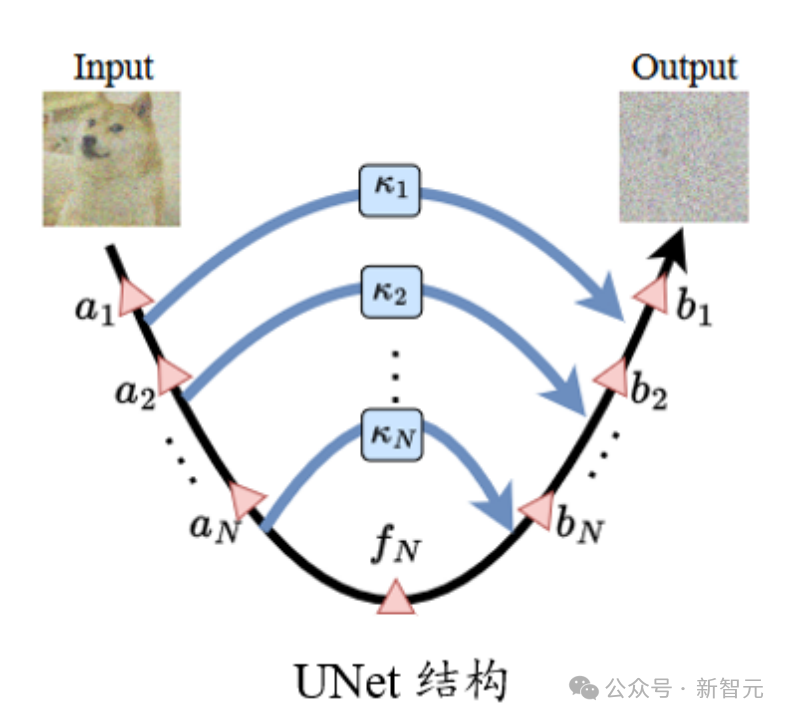
さらに、UNet 構造の特殊性により、浅いフィーチャは長いスキップ接続を通じて深い位置に接続されるため、勾配消失などの問題がさらに回避されます。
では、逆に考えてみると、このような構造に注意しないと、アップデートによる過度の勾配やパラメータ(特徴量)の発振などの問題が発生するのでしょうか?
#写真
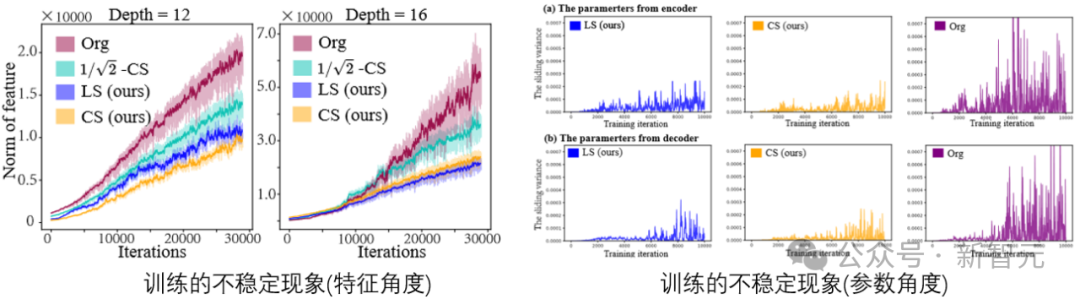 #トレーニング プロセス中に拡散モデル タスクの特性とパラメーターを視覚化すると、次のことがわかります。確かに不安定現象は存在します。
#トレーニング プロセス中に拡散モデル タスクの特性とパラメーターを視覚化すると、次のことがわかります。確かに不安定現象は存在します。
パラメータ (特徴) の不安定性は勾配に影響し、それがパラメータの更新にも影響します。結局のところ、このプロセスには、パフォーマンスに望ましくない干渉が発生するリスクが大きくなります。したがって、この不安定性を制御する方法を見つける必要があります。
さらに、拡散モデルについて。 UNet の入力はノイズを含む画像であり、モデルが追加されたノイズを正確に予測する必要がある場合、追加の外乱に対する入力に対する強力なロバスト性がモデルに必要になります。
論文: https://arxiv.org/abs/2310.13545
定理 3.1 から、中間層の特徴の振動範囲 (上限と下限の幅) は、スケーリング係数の二乗の合計に直接関係します。適切なスケーリング係数は、機能の不安定性を軽減するのに役立ちます。
ただし、スケーリング係数を直接 0 に設定すると、ショックは実際に最適に緩和されることに注意してください。 (手動ドッグヘッド)
しかし、UNet がスキップのない状況に劣化すると、不安定性の問題は解決されますが、表現能力も失われます。これは、モデルの安定性と表現機能の間のトレードオフです。
 写真
写真
同様に、パラメータ勾配の観点から。定理 3.3 は、スケーリング係数が勾配の大きさを制御することも示しています。
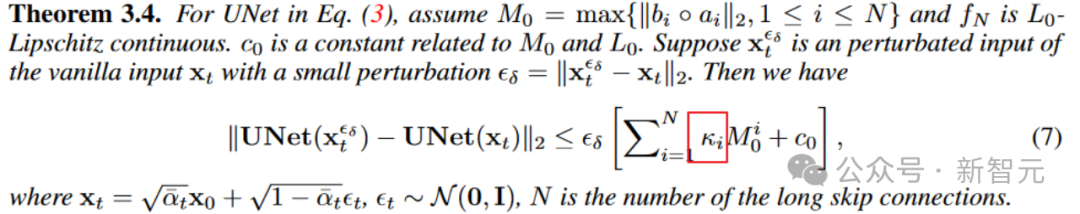 図
図
さらに、定理 3.4 は、ロング スキップ接続のスケーリングが入力外乱に対するモデルのロバスト性に影響を与える可能性があることも示しています。入力外乱に対する拡散モデルの安定性が向上する境界。
スケーリングになる
上記の分析を通じて、安定したモデル トレーニングのためのロング スキップ接続でのスケーリングの重要性を理解しました。 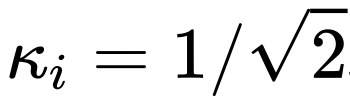 は上記の分析にも当てはまります。
は上記の分析にも当てはまります。
次に、どのような種類のスケーリングがパフォーマンスを向上できるかを分析します。結局のところ、上記の分析は、スケーリングが適切であることを示すだけであり、どのような種類のスケーリングであるかを判断することはできません。最高かそれ以上、良いです。
簡単な方法としては、ロングスキップ接続に学習可能なモジュールを導入し、適応的にスケーリングを調整する方法をLearnable Scaling (LS)法と呼びます。以下に示すように、SENet のような構造を使用します (ここで考慮されている U-ViT 構造は、非常によく組織されています!)
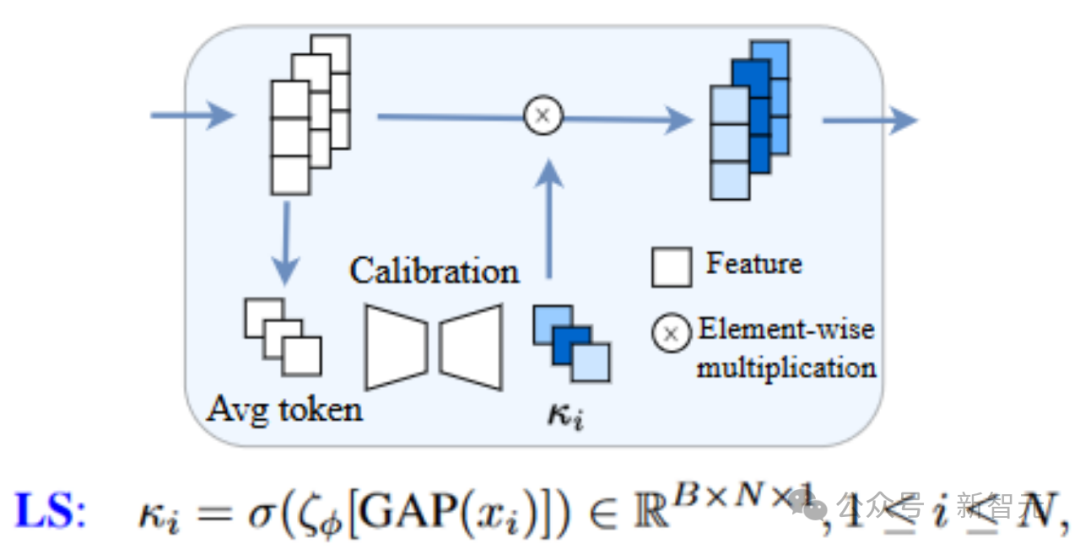 Picture
Picture
この記事の結果から判断すると、LS は確かに拡散モデルのトレーニングを効果的に安定させることができます。さらに、LS で学習した係数の可視化を試みます。
下の図に示すように、これらの係数は指数関数的な下降傾向を示していることがわかります (ここでの最初のロング スキップ接続は、UNet の最初の端と最後の端を接続する接続を指すことに注意してください)。係数がほぼYu 1に近く、この現象もすごいですね!
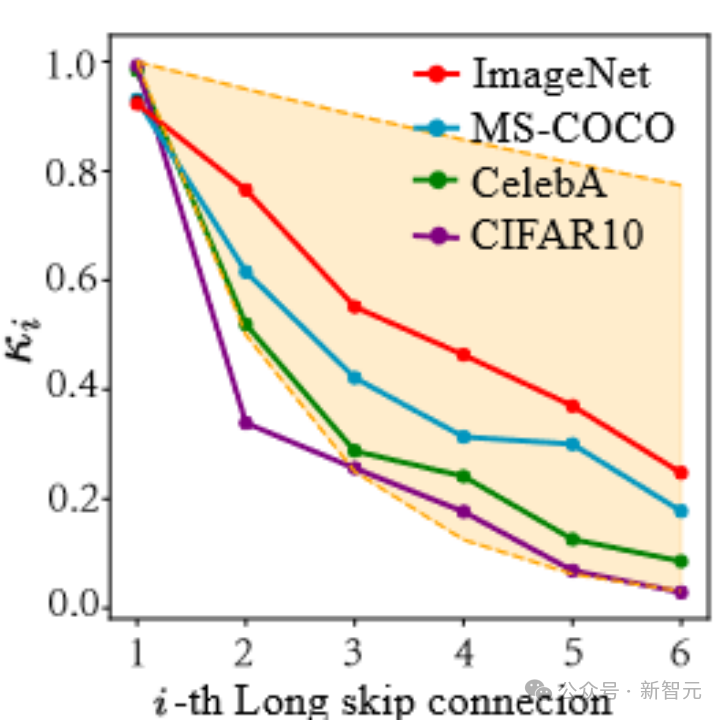 写真
写真
この一連の観察に基づいて (詳細については論文を参照してください)、私たちはさらに Constant Scaling (CS) を提案しました。 ) メソッド、つまり、学習可能なパラメータは必要ありません:
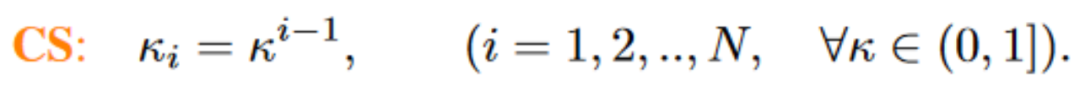
CS 戦略は、次を使用した元のスケーリング操作と同じです。 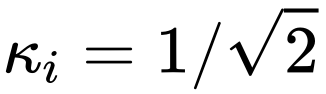 追加のパラメーターを使用しないため、追加の計算コストはほとんどかかりません。
追加のパラメーターを使用しないため、追加の計算コストはほとんどかかりません。
安定したトレーニングでは、ほとんどの場合、CS は LS ほどパフォーマンスが良くありませんが、既存の 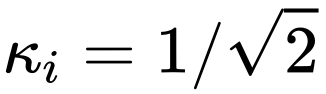 戦略を試してみる価値はあります。
戦略を試してみる価値はあります。
上記の CS と LS の実装は非常に簡単で、必要なコードは数行だけです。各 (hua) 式 (li) および各 (hu) タイプ (shao) の UNet 構造について、フィーチャーの次元を調整する必要がある場合があります。 (手動ドッグヘッド 1)
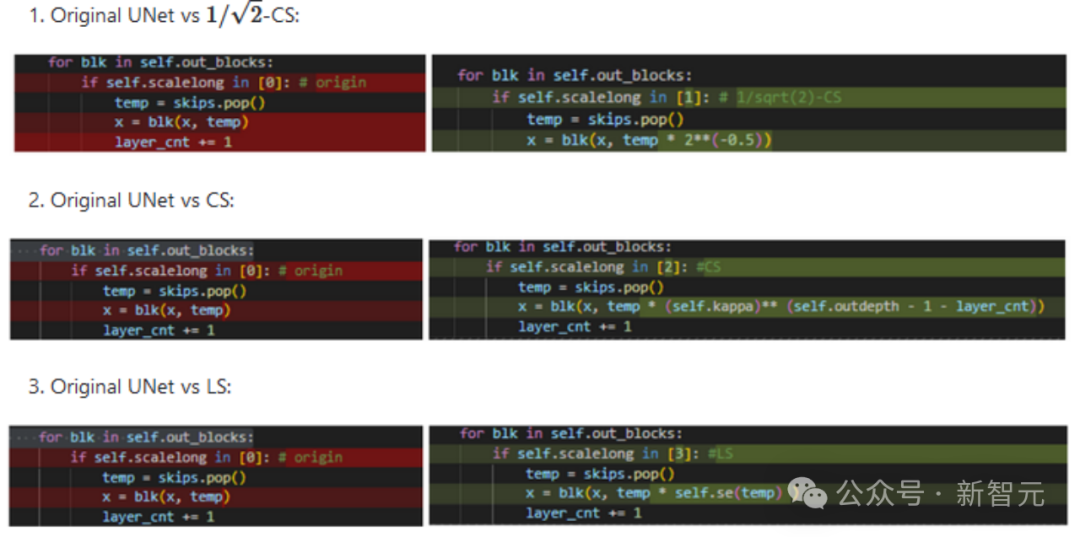
最近、FreeU、SCEdit などのフォローアップ作業でも、スキップ接続でのスケーリングの重要性が明らかになりました。
以上が数行のコードで UNet を安定化! 中山大学などが ScaleLong 普及モデルを提案: Scaling の疑問から Scaling になるまでの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

