
導出連鎖ルールは、機械学習における重要な数学ツールの 1 つです。線形回帰、ロジスティック回帰、ニューラル ネットワークなどのアルゴリズムで広く使用されています。このルールは微積分の連鎖ルールを応用したもので、変数に関する関数の導関数を計算するのに役立ちます。
複合関数 f(x) は複数の単純な関数で構成されており、それぞれの関数には x に関する導関数があります。連鎖則によれば、x に関する f(x) の導関数は、単純な関数の導関数を乗算および加算することによって取得できます。
正式な式は次のとおりです: y=f(u) および u=g(x) の場合、x に関する y の導関数 dy/dx=f'(u) *g'(x)。
この式は、x に関する単純な関数の導関数とそれらの組み合わせを知ることで、x に関する複合関数の導関数を計算できることを示しています。
導出連鎖ルールは、最適化アルゴリズム、特に勾配降下法などの最適化アルゴリズムにおいて重要な役割を果たします。これは、損失関数を最小化するためにモデル パラメーターを更新するために使用されます。連鎖則の中心的な考え方は、関数が複数の単純な関数で構成されている場合、変数に関するこの関数の導関数は、変数に関する各単純な関数の導関数を乗算することによって取得できるということです。機械学習では、このルールはモデル パラメーターに関する損失関数の勾配を計算するために広く使用されています。このアプローチの有効性により、バックプロパゲーション アルゴリズムを介してディープ ニューラル ネットワークを効率的にトレーニングすることができます。
機械学習では、パラメータを最適化する必要があることがよくあります。これには、パラメータに関する損失関数の導関数を解くことが含まれます。損失関数は通常、複数の単純な関数で構成される複合関数であるため、連鎖則を使用してパラメータに関する損失関数の導関数を計算する必要があります。
単純な線形回帰モデルがあるとします。モデルの出力 y は入力 x の線形結合、つまり y=Wx b です。ここで、W と b はモデルのパラメータ。損失関数 L(y,t) (t が真のラベル) がある場合、連鎖ルールを介してモデル パラメーターに関する損失関数の勾配を計算できます。
dL/dW= dL/dy*dy/dW
##dL/db=dL/dy*dy/db ここで dL/ dy は出力の損失関数です。dy/dW および dy/db は、パラメーターに関するモデルの出力の微分です。この式を通じて、モデル パラメーターの損失関数の勾配を計算し、勾配降下法などの最適化アルゴリズムを使用してモデルのパラメーターを更新して損失関数を最小限に抑えることができます。 ニューラル ネットワークなどのより複雑なモデルでは、連鎖規則も広く使用されています。ニューラル ネットワークは通常、複数の非線形層と線形層で構成され、それぞれが独自のパラメーターを持ちます。損失関数を最小化するようにモデルのパラメーターを最適化するには、連鎖則を使用して各パラメーターの損失関数の勾配を計算する必要があります。 つまり、導出連鎖ルールは機械学習における非常に重要な数学的ツールの 1 つであり、特定の変数に関する複合関数の導関数を計算するのに役立ちます。次に、それを使用してモデルのパラメータを最適化し、損失関数を最小限に抑えます。以上が機械学習における連鎖導出ルールの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 個人的なハッキングはかなり激しいクマになりますMay 11, 2025 am 11:09 AM
個人的なハッキングはかなり激しいクマになりますMay 11, 2025 am 11:09 AMサイバー攻撃が進化しています。 一般的なフィッシングメールの時代は終わりました。 サイバー犯罪の将来は超個人化されており、高度にターゲットを絞った攻撃を作成するために、容易に利用可能なオンラインデータとAIを活用しています。 あなたの仕事を知っている詐欺師を想像してください、あなたのf
 教皇レオXIVは、AIが彼の名前の選択にどのように影響したかを明らかにしますMay 11, 2025 am 11:07 AM
教皇レオXIVは、AIが彼の名前の選択にどのように影響したかを明らかにしますMay 11, 2025 am 11:07 AM枢機of大学への彼の就任演説では、シカゴ生まれのロバート・フランシス・プレボスト、新たに選出された教皇レオ14世は、彼の同名の教皇レオXIIIの影響について議論しました。
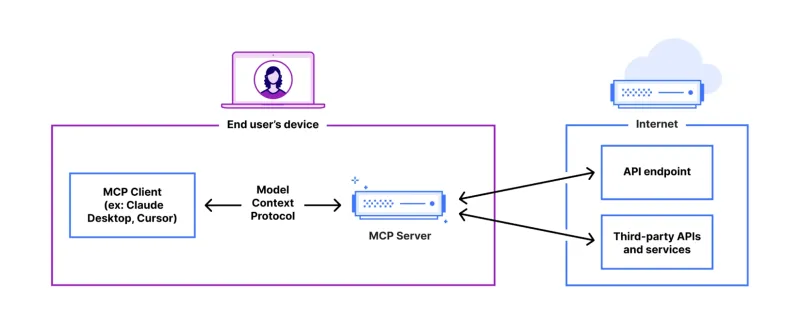 初心者および専門家向けのFastapi -MCPチュートリアル-Analytics VidhyaMay 11, 2025 am 10:56 AM
初心者および専門家向けのFastapi -MCPチュートリアル-Analytics VidhyaMay 11, 2025 am 10:56 AMこのチュートリアルでは、モデルコンテキストプロトコル(MCP)とFastAPIを使用して、大規模な言語モデル(LLM)と外部ツールを統合する方法を示しています。 FastAPIを使用して簡単なWebアプリケーションを構築し、それをMCPサーバーに変換し、Lを有効にします
 DIA-1.6B TTS:最高のテキストからダイアログの生成モデル - 分析VidhyaMay 11, 2025 am 10:27 AM
DIA-1.6B TTS:最高のテキストからダイアログの生成モデル - 分析VidhyaMay 11, 2025 am 10:27 AMDIA-1.6Bを探索:資金がゼロの2人の学部生によって開発された画期的なテキストからスピーチモデル! この16億個のパラメーターモデルは、笑い声やくしゃみなどの非言語的手がかりを含む、非常に現実的なスピーチを生成します。この記事ガイド
 AIがメンターシップをこれまで以上に意味のあるものにする3つの方法May 10, 2025 am 11:17 AM
AIがメンターシップをこれまで以上に意味のあるものにする3つの方法May 10, 2025 am 11:17 AM私は心から同意します。 私の成功は、メンターの指導に密接に関連しています。 特にビジネス管理に関する彼らの洞察は、私の信念と実践の基盤を形成しました。 この経験は、メンターへの私のコミットメントを強調しています
 AIは、鉱業で新しい可能性を発掘しますMay 10, 2025 am 11:16 AM
AIは、鉱業で新しい可能性を発掘しますMay 10, 2025 am 11:16 AMAIはマイニング機器を強化しました 採掘操作環境は厳しく危険です。人工知能システムは、最も危険な環境から人間を排除し、人間の能力を高めることにより、全体的な効率とセキュリティを改善するのに役立ちます。人工知能は、マイニング操作で使用される自動運転トラック、ドリル、ローダーの電源にますます使用されています。 これらのAI搭載車両は、危険な環境で正確に動作し、それにより安全性と生産性が向上します。一部の企業は、大規模な鉱業作業のために自動鉱業車両を開発しています。 挑戦的な環境で動作する機器には、継続的なメンテナンスが必要です。ただし、メンテナンスは重要なデバイスをオフラインに保ち、リソースを消費する可能性があります。より正確なメンテナンスとは、高価で必要な機器の稼働時間が増加し、大幅なコスト削減を意味します。 AI駆動型
 AIエージェントが25年で最大の職場革命を引き起こす理由May 10, 2025 am 11:15 AM
AIエージェントが25年で最大の職場革命を引き起こす理由May 10, 2025 am 11:15 AMSalesforceのCEOであるMarc Benioffは、AIエージェントが推進する記念碑的な職場革命、Salesforceとその顧客ベース内ですでに進行中の変革を予測しています。 彼は、従来の市場から、に焦点を当てた非常に大きな市場への移行を想定しています
 ai hrは、aiの養子縁組が舞い上がるので私たちの世界を揺るがそうとしていますMay 10, 2025 am 11:14 AM
ai hrは、aiの養子縁組が舞い上がるので私たちの世界を揺るがそうとしていますMay 10, 2025 am 11:14 AMHRでのAIの台頭:ロボットの同僚との労働力をナビゲートする AIと人事(HR)への統合は、もはや未来の概念ではありません。急速に新しい現実になりつつあります。 このシフトは、人事の専門家と従業員の両方のDEMに影響を与えます


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

Dreamweaver Mac版
ビジュアル Web 開発ツール

MantisBT
Mantis は、製品の欠陥追跡を支援するために設計された、導入が簡単な Web ベースの欠陥追跡ツールです。 PHP、MySQL、Web サーバーが必要です。デモおよびホスティング サービスをチェックしてください。

SublimeText3 中国語版
中国語版、とても使いやすい

SublimeText3 英語版
推奨: Win バージョン、コードプロンプトをサポート!






