
ニューラルネットワーク遺伝的アルゴリズム関数極値最適化は、遺伝的アルゴリズムとニューラルネットワークを総合的に利用した最適化アルゴリズムです。その中心的なアイデアは、ニューラル ネットワーク モデルを使用して目的関数を近似し、遺伝的アルゴリズムを通じて最適なソリューションを検索することです。他の最適化アルゴリズムと比較して、ニューラル ネットワーク遺伝的アルゴリズムは、強力なグローバル検索機能と堅牢性を備えており、複雑な非線形関数の極値問題を効率的に解決できます。このアルゴリズムの利点は、ニューラル ネットワークの学習能力を通じて複雑な目的関数を近似し、遺伝的アルゴリズムの探索戦略を通じて最適解をグローバルに探索できることです。ニューラル ネットワークと遺伝的アルゴリズムの利点を最大限に活用することにより、ニューラル ネットワークの遺伝的アルゴリズム関数の極値最適化は、実用的な応用において幅広い可能性を秘めています。
未知の非線形関数の場合、関数の入力データと出力データだけから関数の極値を正確に見つけることは困難です。このような問題を解決するには、遺伝的アルゴリズムと組み合わせたニューラルネットワークの手法を使用できます。ニューラル ネットワークには非線形フィッティング機能があり、関数をフィッティングできます。遺伝的アルゴリズムには非線形最適化機能があり、関数の極点を検索できます。これら 2 つの方法を組み合わせることで、関数の極値をより正確に求めることができます。
ニューラル ネットワークの遺伝的アルゴリズム関数の極値の最適化は、主に BP ニューラル ネットワークのトレーニングとフィッティング、および遺伝的アルゴリズムの極値の最適化の 2 つのステップに分かれています。
まず、BP ニューラル ネットワークを使用して入力データをトレーニングおよび適合します。学習プロセスを通じて、ニューラル ネットワークは目的関数を近似し、出力結果を予測できます。このステップの主な目標は、ニューラル ネットワークをトレーニングして、入力データを正確に適合させ、問題を最適な解決策を見つける問題に変換できるようにすることです。
次に、遺伝的アルゴリズムを使用してニューラル ネットワークの重みを調整し、選択、交差、突然変異などの操作を使用して最適なソリューションを見つけます。このステップの主な目的は、遺伝的アルゴリズムのグローバル検索特性と堅牢性を使用して、ニューラル ネットワークの重みの最適な組み合わせを見つけ、ニューラル ネットワークの予測出力が最高のレベルに達するようにすることです。
上記の 2 つのステップを通じて、ニューラル ネットワークの遺伝的アルゴリズム関数の極値最適化は、非線形関数の極値問題を最適解を見つける問題に変換し、ニューラル ネットワークと遺伝的アルゴリズムを使用することができます。このアルゴリズムの利点は、最適な解決策を見つけられることです。
ニューラル ネットワークの遺伝的アルゴリズム関数の極値最適化は、構造、層の数、ノードの数、活性化関数など、特定の問題に合わせてカスタマイズおよび最適化する必要があることに注意してください。ニューラルネットワークのパラメータ選択、遺伝的アルゴリズムのパラメータ設定など同時に、複雑な問題の場合、より良い最適化結果を得るためにアルゴリズムのパラメーターと構造を調整する必要がある場合があります。
ニューラル ネットワークの遺伝的アルゴリズム関数の極値最適化の例
非線形関数 f(x,y)=x^ 2 y があるとします。 ^2、この関数の最小点を見つけたいと考えています。
まず、ニューラル ネットワークを使用してこの関数を当てはめることができます。入力層 (2 ノード、x と y に対応)、隠れ層 (5 ノード)、出力層 (1 ノード、関数の出力値に対応) などの単純なニューラル ネットワーク構造を選択します。 4000 セットのトレーニング データを使用し、BP ニューラル ネットワークを介してトレーニングおよび適合し、ニューラル ネットワークに関数 f(x,y) のルールを学習させます。
次に、遺伝的アルゴリズムを使用して、トレーニングされたニューラル ネットワークを最適化します。ニューラルネットワークの重みを個体とみなして、各個体は適応度を持ち、この適応度がニューラルネットワークが予測する出力値となります。最適な個体、つまりニューラルネットワークの重みの最適な組み合わせが見つかるまで、選択、交叉、突然変異などの操作を通じて個体の最適化を続けます。
ニューラル ネットワークの遺伝的アルゴリズム関数の極値最適化を通じて、関数 f(x,y) の最小値点を見つけることができます。この最小点に対応する入力値が、ニューラルネットワークの重みの最適な組み合わせに対応する入力値である。対応する実装プロセスは次のとおりです:
import numpy as np
from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from scipy.optimize import minimize
# 定义目标函数
def f(x):
return x[0]**2 + x[1]**2
# 生成训练数据和测试数据
X = np.random.rand(4000, 2)
y = f(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 训练神经网络
mlp = MLPRegressor(hidden_layer_sizes=(5,), activation='relu', solver='adam', max_iter=1000)
mlp.fit(X_train, y_train)
# 定义遗传算法优化函数
def nnga_optimize(x0):
# 定义适应度函数
def fitness(x):
return -f(x) # 适应度函数取负值,因为我们要找极小值点
# 定义遗传算法参数
args = (mlp.coefs_, mlp.intercepts_)
options = {'maxiter': 1000}
# 定义约束条件,限制搜索范围在一个小区域内
bounds = [(0, 1), (0, 1)]
# 使用scipy的minimize函数进行优化
res = minimize(fitness, x0, args=args, bounds=bounds, method='SLSQP', options=options)
return res.x
# 进行遗传算法优化,找到最优解
x_opt = nnga_optimize([0.5, 0.5])
print('最优解:', x_opt)以上がニューラルネットワーク遺伝的アルゴリズムを使用して関数の極値問題を解決するの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 解析二元神经网络的功能和原理Jan 22, 2024 pm 03:00 PM
解析二元神经网络的功能和原理Jan 22, 2024 pm 03:00 PM二元神经网络(BinaryNeuralNetworks,BNN)是一种神经网络,其神经元仅具有两个状态,即0或1。相对于传统的浮点数神经网络,BNN具有许多优点。首先,BNN可以利用二进制算术和逻辑运算,加快训练和推理速度。其次,BNN减少了内存和计算资源的需求,因为二进制数相对于浮点数来说需要更少的位数来表示。此外,BNN还具有提高模型的安全性和隐私性的潜力。由于BNN的权重和激活值仅为0或1,其模型参数更难以被攻击者分析和逆向工程。因此,BNN在一些对数据隐私和模型安全性有较高要求的应用中具
 探究RNN、LSTM和GRU的概念、区别和优劣Jan 22, 2024 pm 07:51 PM
探究RNN、LSTM和GRU的概念、区别和优劣Jan 22, 2024 pm 07:51 PM在时间序列数据中,观察之间存在依赖关系,因此它们不是相互独立的。然而,传统的神经网络将每个观察看作是独立的,这限制了模型对时间序列数据的建模能力。为了解决这个问题,循环神经网络(RNN)被引入,它引入了记忆的概念,通过在网络中建立数据点之间的依赖关系来捕捉时间序列数据的动态特性。通过循环连接,RNN可以将之前的信息传递到当前观察中,从而更好地预测未来的值。这使得RNN成为处理时间序列数据任务的强大工具。但是RNN是如何实现这种记忆的呢?RNN通过神经网络中的反馈回路实现记忆,这是RNN与传统神经
 计算神经网络的浮点操作数(FLOPS)Jan 22, 2024 pm 07:21 PM
计算神经网络的浮点操作数(FLOPS)Jan 22, 2024 pm 07:21 PMFLOPS是计算机性能评估的标准之一,用来衡量每秒的浮点运算次数。在神经网络中,FLOPS常用于评估模型的计算复杂度和计算资源的利用率。它是一个重要的指标,用来衡量计算机的计算能力和效率。神经网络是一种复杂的模型,由多层神经元组成,用于进行数据分类、回归和聚类等任务。训练和推断神经网络需要进行大量的矩阵乘法、卷积等计算操作,因此计算复杂度非常高。FLOPS(FloatingPointOperationsperSecond)可以用来衡量神经网络的计算复杂度,从而评估模型的计算资源使用效率。FLOP
 模糊神经网络的定义和结构解析Jan 22, 2024 pm 09:09 PM
模糊神经网络的定义和结构解析Jan 22, 2024 pm 09:09 PM模糊神经网络是一种将模糊逻辑和神经网络结合的混合模型,用于解决传统神经网络难以处理的模糊或不确定性问题。它的设计受到人类认知中模糊性和不确定性的启发,因此被广泛应用于控制系统、模式识别、数据挖掘等领域。模糊神经网络的基本架构由模糊子系统和神经子系统组成。模糊子系统利用模糊逻辑对输入数据进行处理,将其转化为模糊集合,以表达输入数据的模糊性和不确定性。神经子系统则利用神经网络对模糊集合进行处理,用于分类、回归或聚类等任务。模糊子系统和神经子系统之间的相互作用使得模糊神经网络具备更强大的处理能力,能够
 改进的RMSprop算法Jan 22, 2024 pm 05:18 PM
改进的RMSprop算法Jan 22, 2024 pm 05:18 PMRMSprop是一种广泛使用的优化器,用于更新神经网络的权重。它是由GeoffreyHinton等人在2012年提出的,并且是Adam优化器的前身。RMSprop优化器的出现主要是为了解决SGD梯度下降算法中遇到的一些问题,例如梯度消失和梯度爆炸。通过使用RMSprop优化器,可以有效地调整学习速率,并且自适应地更新权重,从而提高深度学习模型的训练效果。RMSprop优化器的核心思想是对梯度进行加权平均,以使不同时间步的梯度对权重的更新产生不同的影响。具体而言,RMSprop会计算每个参数的平方
 浅层特征与深层特征的结合在实际应用中的示例Jan 22, 2024 pm 05:00 PM
浅层特征与深层特征的结合在实际应用中的示例Jan 22, 2024 pm 05:00 PM深度学习在计算机视觉领域取得了巨大成功,其中一项重要进展是使用深度卷积神经网络(CNN)进行图像分类。然而,深度CNN通常需要大量标记数据和计算资源。为了减少计算资源和标记数据的需求,研究人员开始研究如何融合浅层特征和深层特征以提高图像分类性能。这种融合方法可以利用浅层特征的高计算效率和深层特征的强表示能力。通过将两者结合,可以在保持较高分类准确性的同时降低计算成本和数据标记的要求。这种方法对于那些数据量较小或计算资源有限的应用场景尤为重要。通过深入研究浅层特征和深层特征的融合方法,我们可以进一
 蒸馏模型的基本概念Jan 22, 2024 pm 02:51 PM
蒸馏模型的基本概念Jan 22, 2024 pm 02:51 PM模型蒸馏是一种将大型复杂的神经网络模型(教师模型)的知识转移到小型简单的神经网络模型(学生模型)中的方法。通过这种方式,学生模型能够从教师模型中获得知识,并且在表现和泛化性能方面得到提升。通常情况下,大型神经网络模型(教师模型)在训练时需要消耗大量计算资源和时间。相比之下,小型神经网络模型(学生模型)具备更高的运行速度和更低的计算成本。为了提高学生模型的性能,同时保持较小的模型大小和计算成本,可以使用模型蒸馏技术将教师模型的知识转移给学生模型。这种转移过程可以通过将教师模型的输出概率分布作为学生
 SqueezeNet简介及其特点Jan 22, 2024 pm 07:15 PM
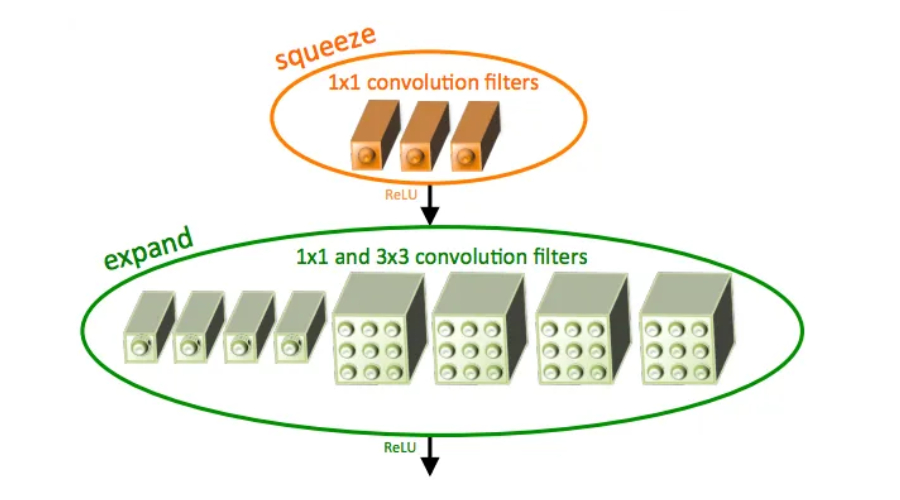
SqueezeNet简介及其特点Jan 22, 2024 pm 07:15 PMSqueezeNet是一种小巧而精确的算法,它在高精度和低复杂度之间达到了很好的平衡,因此非常适合资源有限的移动和嵌入式系统。2016年,DeepScale、加州大学伯克利分校和斯坦福大学的研究人员提出了一种紧凑高效的卷积神经网络(CNN)——SqueezeNet。近年来,研究人员对SqueezeNet进行了多次改进,其中包括SqueezeNetv1.1和SqueezeNetv2.0。这两个版本的改进不仅提高了准确性,还降低了计算成本。SqueezeNetv1.1在ImageNet数据集上的精度


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

DVWA
Damn Vulnerable Web App (DVWA) は、非常に脆弱な PHP/MySQL Web アプリケーションです。その主な目的は、セキュリティ専門家が法的環境でスキルとツールをテストするのに役立ち、Web 開発者が Web アプリケーションを保護するプロセスをより深く理解できるようにし、教師/生徒が教室環境で Web アプリケーションを教え/学習できるようにすることです。安全。 DVWA の目標は、シンプルでわかりやすいインターフェイスを通じて、さまざまな難易度で最も一般的な Web 脆弱性のいくつかを実践することです。このソフトウェアは、

PhpStorm Mac バージョン
最新(2018.2.1)のプロフェッショナル向けPHP統合開発ツール

AtomエディタMac版ダウンロード
最も人気のあるオープンソースエディター

MinGW - Minimalist GNU for Windows
このプロジェクトは osdn.net/projects/mingw に移行中です。引き続きそこでフォローしていただけます。 MinGW: GNU Compiler Collection (GCC) のネイティブ Windows ポートであり、ネイティブ Windows アプリケーションを構築するための自由に配布可能なインポート ライブラリとヘッダー ファイルであり、C99 機能をサポートする MSVC ランタイムの拡張機能が含まれています。すべての MinGW ソフトウェアは 64 ビット Windows プラットフォームで実行できます。

ホットトピック
 7446
7446 15
15 1374
1374 52
52



