matlab を使用して微分方程式の初期値問題を解きます 数値解と解析解の範囲は区間で描画されます
matlab を使用して微分方程式 5261 数値解 4102 初期値問題と解析解を解くと、次のように処理できます。
1. 数値解
微分方程式の初期値問題の数値解は、関数 ode を使用して解くことができます。
まず、微分方程式の関数、つまり
をカスタマイズします。dy = 3/x*y x^3*(exp(x) cos(x))-2*x;
2 番目に、初期条件を決定します。つまり、
y0=[(exp(pi) 2/pi)*pi^3];
3 番目に、ode45 関数を使用して数値解 [x, y]
を取得します。2. 分析ソリューション
微分方程式の初期値問題の解析的解は、関数 dsolve を使用して解くことができます。
最初に、y(x) の変数、つまり
を宣言します。シムズy(x)
2 番目、y(x) の 1 次導関数、つまり
Dy=diff(y,1)
3 番目に、関数 dsolve を使用して、解析解 y(x) の式を求めます。
y=dsolve(Dy==3/x*y x^3*(exp(x) cos(x))-2*x,y(pi)==(exp(pi) 2/pi)*pi ^3)
3. 数値解と解析解曲線を描く
まず、plot関数を使って数値解の曲線を描きます
プロット(x.y)
2 番目に、[π, 2π] 区間の x の一連のいくつかの値と y
に相当する y 値を計算します。第三に、プロット機能を使用して分析解の曲線を描きます
コードを実行すると、次の結果が得られます。
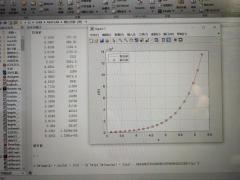
MATLABの質問
%%%%%%%%%%%%%%%%%%%ソースプログラム
i=0;equ=0;sum=0;
data=input('番号を入力してください: ');
while(データ~=0)
sum=合計データ;
key=input('続けてください: ');
データ=キー;
i=i1;
###終わり###equ=sum/i;
等価、合計
%%%%%%%%%%%%%%%%%%%%%%%%%%
結果:
数字を入力してください: 1
続けてください: 2
続けてください: 3
続けてください: 4
続けてください: 5
続けてください:0
equ =
3
合計 =
15
以上がMatlab の実装方法と、区間内の微分方程式の初期値問題に対する数値解および解析解のグラフィック表示の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 ChatGptに最適なVPNはどれですか? - ミニトールApr 29, 2025 am 12:50 AM
ChatGptに最適なVPNはどれですか? - ミニトールApr 29, 2025 am 12:50 AMサポートされていない国、地域、または領土でVPNを介してChatGptを使用したい場合、ChatGPTに最適なVPNをご存知ですか?この投稿では、PHP.CNソフトウェアでいくつかの良い選択肢を紹介します。要件に応じて1つを選択できます
 xboxpcappft.exe悪い画像エラー:修正方法は次のとおりです。Apr 29, 2025 am 12:49 AM
xboxpcappft.exe悪い画像エラー:修正方法は次のとおりです。Apr 29, 2025 am 12:49 AMWindows 11/10で「xboxpcappft.exeバッド画像」の問題を修正する方法は? PHP.CNからのこの投稿では、迷惑な問題を解決するための複数の方法を提示します。読書を続けてください。
 OneDriveファイルを修正する方法Windows10/11 -Minitoolを削除することはできませんApr 29, 2025 am 12:48 AM
OneDriveファイルを修正する方法Windows10/11 -Minitoolを削除することはできませんApr 29, 2025 am 12:48 AMOneDriveでファイルまたはフォルダーを削除する場合はどうすればよいですか?ただし、OneDriveファイルまたはフォルダーを削除できないことがわかりますか?これで、この投稿をPHP.CNから読んで、「OneDriveファイルをWindows1で削除することはできません。
 ディスプレイ接続が制限される場合があります:主要な要因とソリューションApr 29, 2025 am 12:47 AM
ディスプレイ接続が制限される場合があります:主要な要因とソリューションApr 29, 2025 am 12:47 AMエラーメッセージ「表示接続が制限される可能性があります」は、デバイスを起動する際に迷惑な問題です。 PHP.CNからのこの投稿では、この問題の原因とそれを迅速に解決する方法に関する詳細情報を入手できます。
 Windows11 Build 25115は、開発チャネルのインサイダーにリリースされます-MinitoolApr 29, 2025 am 12:46 AM
Windows11 Build 25115は、開発チャネルのインサイダーにリリースされます-MinitoolApr 29, 2025 am 12:46 AMMicrosoftは、開発チャンネルのインサイダーに新しいビルドをリリースし、Windows 11 Build 25115です。これは、ベータチャネルにリリースされたビルドと比較してより高いビルドです。このPHP.CN投稿に従って、関連情報に関するいくつかの情報を学習できます。
 データを失うことなくWindows11/10でCドライブを掃除する方法-MINITOOLApr 29, 2025 am 12:45 AM
データを失うことなくWindows11/10でCドライブを掃除する方法-MINITOOLApr 29, 2025 am 12:45 AMCドライブのスペースを解放するにはどうすればよいですか、またはCドライブで廃棄物をクリアするにはどうすればよいですか?これは、PHP.CNがここで焦点を当てているトピックです。 Cドライブが古いアプリと不必要なプログラムがいっぱいになっている場合は、クリーンアップを選択できます。始めましょう。
 chatgpt 4 vs. chatgpt 3:それらの違い-minitoolApr 29, 2025 am 12:44 AM
chatgpt 4 vs. chatgpt 3:それらの違い-minitoolApr 29, 2025 am 12:44 AMChatGPTはGPT-4で更新されました。この更新をよりよく理解するために、ChatGPT 4とChatGPT 3の違いを紹介します。さらに、Windowsで削除されたファイルを回復する場合は、PHP.CN Power Data Recoveryを試すことができます。
 メディア機能パックWindows11ダウンロード&インストール:パワー戦術Apr 29, 2025 am 12:43 AM
メディア機能パックWindows11ダウンロード&インストール:パワー戦術Apr 29, 2025 am 12:43 AMWindows 11 nまたはknエディションを使用している場合、どのようにしてメディア機能パックをダウンロードしてインストールできますか? この投稿では、PHP.CNは、Windows 11 Media Feature Packの取得に関する段階的なガイドを提供しています。いくつかの詳細を見てみましょう。


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

EditPlus 中国語クラック版
サイズが小さく、構文の強調表示、コード プロンプト機能はサポートされていません

VSCode Windows 64 ビットのダウンロード
Microsoft によって発売された無料で強力な IDE エディター

SecLists
SecLists は、セキュリティ テスターの究極の相棒です。これは、セキュリティ評価中に頻繁に使用されるさまざまな種類のリストを 1 か所にまとめたものです。 SecLists は、セキュリティ テスターが必要とする可能性のあるすべてのリストを便利に提供することで、セキュリティ テストをより効率的かつ生産的にするのに役立ちます。リストの種類には、ユーザー名、パスワード、URL、ファジング ペイロード、機密データ パターン、Web シェルなどが含まれます。テスターはこのリポジトリを新しいテスト マシンにプルするだけで、必要なあらゆる種類のリストにアクセスできるようになります。

ZendStudio 13.5.1 Mac
強力な PHP 統合開発環境

ホットトピック
 7814
7814 15
15 1646
1646 14
14 1402
1402 52
52 1300
1300 25
25 1237
1237 29
29


