
モンテカルロ シミュレーション手法は、複雑なシステムやプロセスをシミュレートし、その確率分布や特性を取得するために使用される、ランダム サンプリングに基づくシミュレーション手法です。機械学習の分野では、モンテカルロ シミュレーション手法は、コンピューター ビジョン、自然言語処理、強化学習などの問題で広く使用されています。この記事では、いくつかの一般的なモンテカルロ シミュレーション手法のモデルとアルゴリズムを紹介します。
マルコフ連鎖モンテカルロ (MCMC)
マルコフ連鎖モンテカルロは、複素確率を計算するためのマルコフ連鎖 Lowe シミュレーション手法に基づくモンテカルロです。配布物。 MCMC アルゴリズムでは、状態遷移がマルコフ連鎖の特性を満たすことを保証するために、状態遷移確率行列を定義する必要があります。次に、この状態遷移確率行列を使用してサンプルを生成し、これらのサンプルを使用して確率分布を推定できます。
MCMC アルゴリズムの中で、最も一般的に使用されるのは Metropolis-Hastings アルゴリズムです。このアルゴリズムは、提案分布を定義することによって新しいサンプルを生成し、受け入れ確率を使用して新しいサンプルを受け入れるかどうかを決定します。具体的には、合格確率は、新しいサンプルの確率分布の値を古いサンプルの確率分布の値で割った値に、提案された分布の値を乗算した値に等しくなります。受け入れ確率が 1 以上の場合は、新しいサンプルを受け入れます。それ以外の場合は、確率として受け入れ確率を使用して新しいサンプルを受け入れます。このように、新しいサンプルを継続的に生成して受け入れることにより、MCMC アルゴリズムはターゲット分布に収束し、複雑な確率分布のシミュレーションと推定に使用できます。
重要度サンプリング
重要度サンプリングは、サンプリング ベースのモンテカルロ シミュレーション手法であり、複素積分や期待値の計算によく使用されます。重要度サンプリング アルゴリズムでは、サンプルに重みを付ける重要度関数を定義する必要があります。この重要度関数を使用すると、サンプルを生成し、これらのサンプルを使用して期待値または積分を推定できます。重要度サンプリング モデルとアルゴリズムは、サンプリング ベースの重要度サンプリング方法と重要度関数ベースの重要度サンプリング方法の 2 つのタイプに分類できます。サンプリングベースの重要度サンプリングでは、重要度関数からサンプルを抽出し、これらのサンプルを使用して期待値または積分を計算します。重要度関数に基づく重要度サンプリングでは、重要度関数の形式を直接使用して期待値または積分を計算します。どちらの方法にもそれぞれ長所と短所があり、問題の特性に応じて適切な方法を選択することで、計算効率と精度を向上させることができます。
サンプリング ベースの重要度サンプリング アルゴリズムでは、単純な分布からサンプルを抽出し、重要度関数を使用してこれらのサンプルに重み付けを行います。具体的には、ターゲット分布と単純分布を定義し、単純分布からサンプルを抽出し、ターゲット分布上の各サンプルの重みを計算します。最後に、これらのサンプルの重みを使用して期待値または積分を推定します。
重要度関数に基づく重要度サンプリング アルゴリズムでは、サンプルに重み付けする重要度関数を定義します。具体的には、ターゲット分布と重要度関数を定義し、ターゲット分布からサンプルを抽出し、重要度関数を使用してこれらのサンプルに重み付けを行います。最後に、これらの加重サンプルを使用して期待値または積分を推定します。
モンテカルロ木探索 (MCTS)
モンテカルロ木探索は、モンテカルロ シミュレーションに基づく強化学習アルゴリズムであり、問題を解決するためによく使用されます。複雑な意思決定の問題。 MCTS アルゴリズムでは、モンテカルロ シミュレーションを使用して各決定の値を推定し、これらの値を使用して検索ツリーを更新します。具体的には、現在の状態から開始し、モンテカルロ シミュレーションを使用していくつかのサンプルを生成し、これらのサンプルを使用して各決定の値を推定します。次に、これらの値を使用して検索ツリーを更新し、最適な決定を選択します。
確率的勾配ハミルトニアン モンテカルロ法 (SGHMC)
確率的勾配ハミルトニアン モンテカルロ法は、トレーニングの大規模データ セットでよく使用されます。ベイジアン ニューラル ネットワーク。 SGHMC アルゴリズムでは、ハミルトニアン ダイナミクスを使用してシステムの動作をシミュレートし、確率的勾配降下法を使用してパラメーターを更新します。具体的には、システムのエネルギーを記述するハミルトニアン関数を定義し、ハミルトニアン ダイナミクスを使用してシステムの動作をシミュレートします。同時に、確率的勾配降下法を使用してパラメーターを更新し、確率的勾配を使用して各サンプルの勾配を推定します。最後に、これらのサンプルを使用してモデルのパラメーター分布を推定します。
つまり、モンテカルロ シミュレーション手法は機械学習で広く使用されており、多くの複雑な問題の解決に役立ちます。これらの方法にはさまざまなモデルとアルゴリズムがありますが、その中心的なアイデアは、確率分布、期待値、または積分を推定するためのランダムサンプリングに基づいています。機械学習テクノロジーが発展し続けるにつれて、モンテカルロ シミュレーション手法は、より複雑な問題の解決に役立つ重要な役割を果たし続けるでしょう。
以上がモンテカルロ シミュレーションの一般的なモデルとアルゴリズムの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 迅速なエンジニアリングにおける思考のグラフは何ですかApr 13, 2025 am 11:53 AM
迅速なエンジニアリングにおける思考のグラフは何ですかApr 13, 2025 am 11:53 AM導入 迅速なエンジニアリングでは、「思考のグラフ」とは、グラフ理論を使用してAIの推論プロセスを構造化および導く新しいアプローチを指します。しばしば線形sを含む従来の方法とは異なります
 Genaiエージェントとの電子メールマーケティングを組織に最適化しますApr 13, 2025 am 11:44 AM
Genaiエージェントとの電子メールマーケティングを組織に最適化しますApr 13, 2025 am 11:44 AM導入 おめでとう!あなたは成功したビジネスを運営しています。ウェブページ、ソーシャルメディアキャンペーン、ウェビナー、会議、無料リソース、その他のソースを通じて、毎日5000の電子メールIDを収集します。次の明白なステップはです
 Apache Pinotによるリアルタイムアプリのパフォーマンス監視Apr 13, 2025 am 11:40 AM
Apache Pinotによるリアルタイムアプリのパフォーマンス監視Apr 13, 2025 am 11:40 AM導入 今日のペースの速いソフトウェア開発環境では、最適なアプリケーションパフォーマンスが重要です。応答時間、エラーレート、リソース利用などのリアルタイムメトリックを監視することで、メインに役立ちます
 ChatGptは10億人のユーザーにヒットしますか? 「わずか数週間で2倍になりました」とOpenai CEOは言いますApr 13, 2025 am 11:23 AM
ChatGptは10億人のユーザーにヒットしますか? 「わずか数週間で2倍になりました」とOpenai CEOは言いますApr 13, 2025 am 11:23 AM「ユーザーは何人いますか?」彼は突き出した。 「私たちが最後に言ったのは毎週5億人のアクティブであり、非常に急速に成長していると思います」とアルトマンは答えました。 「わずか数週間で2倍になったと言った」とアンダーソンは続けた。 「私はそのprivと言いました
 PIXTRAL -12B:Mistral AI'の最初のマルチモーダルモデル-Analytics VidhyaApr 13, 2025 am 11:20 AM
PIXTRAL -12B:Mistral AI'の最初のマルチモーダルモデル-Analytics VidhyaApr 13, 2025 am 11:20 AM導入 Mistralは、最初のマルチモーダルモデル、つまりPixtral-12B-2409をリリースしました。このモデルは、Mistralの120億個のパラメーターであるNemo 12bに基づいて構築されています。このモデルを際立たせるものは何ですか?これで、画像とTexの両方を採用できます
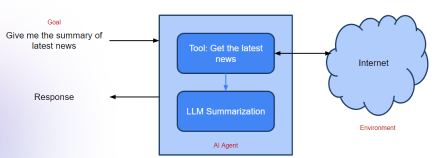 生成AIアプリケーションのエージェントフレームワーク - 分析VidhyaApr 13, 2025 am 11:13 AM
生成AIアプリケーションのエージェントフレームワーク - 分析VidhyaApr 13, 2025 am 11:13 AMクエリに応答するだけでなく、情報を自律的に収集し、タスクを実行し、テキスト、画像、コードなどの複数のタイプのデータを処理するAIを搭載したアシスタントがいることを想像してください。未来的に聞こえますか?これでa
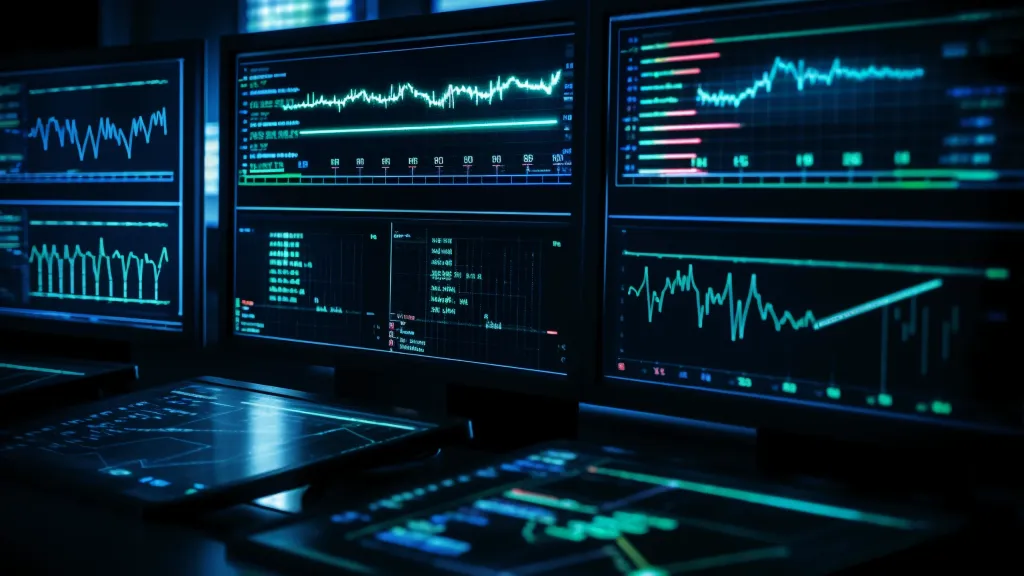 金融セクターにおける生成AIの応用Apr 13, 2025 am 11:12 AM
金融セクターにおける生成AIの応用Apr 13, 2025 am 11:12 AM導入 金融業界は、効率的な取引と信用の可用性を促進することにより経済成長を促進するため、あらゆる国の発展の基礎となっています。取引の容易さとクレジット
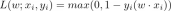 オンライン学習とパッシブアグレッシブアルゴリズムのガイドApr 13, 2025 am 11:09 AM
オンライン学習とパッシブアグレッシブアルゴリズムのガイドApr 13, 2025 am 11:09 AM導入 データは、ソーシャルメディア、金融取引、eコマースプラットフォームなどのソースから前例のないレートで生成されています。この連続的な情報ストリームを処理することは課題ですが、


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

SAP NetWeaver Server Adapter for Eclipse
Eclipse を SAP NetWeaver アプリケーション サーバーと統合します。

AtomエディタMac版ダウンロード
最も人気のあるオープンソースエディター

ZendStudio 13.5.1 Mac
強力な PHP 統合開発環境

VSCode Windows 64 ビットのダウンロード
Microsoft によって発売された無料で強力な IDE エディター

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境







