
ベイジアン最適化は、目的関数を最適化するために使用されるブラック ボックス アルゴリズムです。多くの実際的な問題における非凸の高ノイズ問題に適しています。このアルゴリズムは、サロゲート モデル (ガウス プロセスやランダム フォレストなど) を構築することで目的関数を近似し、ベイジアン推論を使用して次のサンプリング ポイントを選択して、サロゲート モデルの不確実性と目的関数の期待値を低減します。ベイジアン最適化では、通常、全体的な最適点を見つけるために必要なサンプリング ポイントが少なくなり、サンプリング ポイントの位置と数を適応的に調整できます。
ベイズ最適化の基本的な考え方は、目的関数の事後分布を計算することで、既存のサンプルに基づいて次のサンプリング ポイントを選択することです。この戦略は、探索と活用のバランスをとります。つまり、未知の領域を探索し、既知の情報を使用して最適化します。
ベイズ最適化は、ハイパーパラメータ調整、モデル選択、特徴選択などの分野、特に深層学習において実際に広く使用されています。ベイジアン最適化を使用すると、モデルのパフォーマンスと速度を効果的に向上させることができ、さまざまな目的関数と制約に柔軟に適応できます。ベイジアン最適化アルゴリズムの独自性は、既存のサンプル データに基づいてモデルを更新し、この情報を使用して次の操作を選択できることにより、最適解をより効率的に探索できることです。したがって、ベイジアン最適化は、多くの最適化問題において推奨される方法となっています。
ベイズ最適化の原則
ベイズ最適化の原則は 4 つのステップに分けることができます。
サロゲート モデルの構築: サンプリングされた値に基づいて目的関数のサロゲート モデルを構築します。サンプル、ガウス プロセスやランダム フォレストなどのモデル。
2. サンプリング ポイントの選択: エージェント モデルの不確実性と目的関数の期待に基づいて、次のサンプリング ポイントを選択するためにいくつかの戦略が使用されます。一般的な戦略には、信頼区間の最小化と期待される改善が含まれます。これらの戦略は特定の状況に適応でき、より正確で効率的なサンプリング プロセスを実現する必要があります。
3. 目的関数のサンプリング: サンプリング ポイントを選択した後、目的関数をサンプリングし、エージェント モデルを更新します。
特定のサンプル数に達するか、特定の停止基準に達するまで、ステップ 2 と 3 を繰り返します。
ベイズ最適化の中核には、サロゲート モデルの構築とサンプリング ポイントの選択が含まれます。サロゲート モデルは、目的関数の構造と特性を理解するのに役立ち、次のサンプリング ポイントの選択をガイドします。サンプリング ポイントの選択は、事後分布を計算することによって最も可能性の高いサンプリング ポイントを選択するベイズ推論に基づいています。この方法では、既存の情報を最大限に活用し、不要なサンプリング ポイントを回避します。
一般に、ベイジアン最適化は、さまざまな実際の問題における非凸問題や高ノイズ問題に適用できる、効率的で柔軟なブラックボックス最適化アルゴリズムです。
以上がベイズ最適化の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 迅速なエンジニアリングにおける思考のグラフは何ですかApr 13, 2025 am 11:53 AM
迅速なエンジニアリングにおける思考のグラフは何ですかApr 13, 2025 am 11:53 AM導入 迅速なエンジニアリングでは、「思考のグラフ」とは、グラフ理論を使用してAIの推論プロセスを構造化および導く新しいアプローチを指します。しばしば線形sを含む従来の方法とは異なります
 Genaiエージェントとの電子メールマーケティングを組織に最適化しますApr 13, 2025 am 11:44 AM
Genaiエージェントとの電子メールマーケティングを組織に最適化しますApr 13, 2025 am 11:44 AM導入 おめでとう!あなたは成功したビジネスを運営しています。ウェブページ、ソーシャルメディアキャンペーン、ウェビナー、会議、無料リソース、その他のソースを通じて、毎日5000の電子メールIDを収集します。次の明白なステップはです
 Apache Pinotによるリアルタイムアプリのパフォーマンス監視Apr 13, 2025 am 11:40 AM
Apache Pinotによるリアルタイムアプリのパフォーマンス監視Apr 13, 2025 am 11:40 AM導入 今日のペースの速いソフトウェア開発環境では、最適なアプリケーションパフォーマンスが重要です。応答時間、エラーレート、リソース利用などのリアルタイムメトリックを監視することで、メインに役立ちます
 ChatGptは10億人のユーザーにヒットしますか? 「わずか数週間で2倍になりました」とOpenai CEOは言いますApr 13, 2025 am 11:23 AM
ChatGptは10億人のユーザーにヒットしますか? 「わずか数週間で2倍になりました」とOpenai CEOは言いますApr 13, 2025 am 11:23 AM「ユーザーは何人いますか?」彼は突き出した。 「私たちが最後に言ったのは毎週5億人のアクティブであり、非常に急速に成長していると思います」とアルトマンは答えました。 「わずか数週間で2倍になったと言った」とアンダーソンは続けた。 「私はそのprivと言いました
 PIXTRAL -12B:Mistral AI'の最初のマルチモーダルモデル-Analytics VidhyaApr 13, 2025 am 11:20 AM
PIXTRAL -12B:Mistral AI'の最初のマルチモーダルモデル-Analytics VidhyaApr 13, 2025 am 11:20 AM導入 Mistralは、最初のマルチモーダルモデル、つまりPixtral-12B-2409をリリースしました。このモデルは、Mistralの120億個のパラメーターであるNemo 12bに基づいて構築されています。このモデルを際立たせるものは何ですか?これで、画像とTexの両方を採用できます
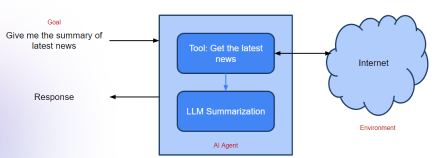 生成AIアプリケーションのエージェントフレームワーク - 分析VidhyaApr 13, 2025 am 11:13 AM
生成AIアプリケーションのエージェントフレームワーク - 分析VidhyaApr 13, 2025 am 11:13 AMクエリに応答するだけでなく、情報を自律的に収集し、タスクを実行し、テキスト、画像、コードなどの複数のタイプのデータを処理するAIを搭載したアシスタントがいることを想像してください。未来的に聞こえますか?これでa
 金融セクターにおける生成AIの応用Apr 13, 2025 am 11:12 AM
金融セクターにおける生成AIの応用Apr 13, 2025 am 11:12 AM導入 金融業界は、効率的な取引と信用の可用性を促進することにより経済成長を促進するため、あらゆる国の発展の基礎となっています。取引の容易さとクレジット
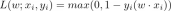 オンライン学習とパッシブアグレッシブアルゴリズムのガイドApr 13, 2025 am 11:09 AM
オンライン学習とパッシブアグレッシブアルゴリズムのガイドApr 13, 2025 am 11:09 AM導入 データは、ソーシャルメディア、金融取引、eコマースプラットフォームなどのソースから前例のないレートで生成されています。この連続的な情報ストリームを処理することは課題ですが、


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

SAP NetWeaver Server Adapter for Eclipse
Eclipse を SAP NetWeaver アプリケーション サーバーと統合します。

DVWA
Damn Vulnerable Web App (DVWA) は、非常に脆弱な PHP/MySQL Web アプリケーションです。その主な目的は、セキュリティ専門家が法的環境でスキルとツールをテストするのに役立ち、Web 開発者が Web アプリケーションを保護するプロセスをより深く理解できるようにし、教師/生徒が教室環境で Web アプリケーションを教え/学習できるようにすることです。安全。 DVWA の目標は、シンプルでわかりやすいインターフェイスを通じて、さまざまな難易度で最も一般的な Web 脆弱性のいくつかを実践することです。このソフトウェアは、

SublimeText3 英語版
推奨: Win バージョン、コードプロンプトをサポート!

メモ帳++7.3.1
使いやすく無料のコードエディター

AtomエディタMac版ダウンロード
最も人気のあるオープンソースエディター







