ホームページ >バックエンド開発 >Python チュートリアル >Python を使用してミニバッチ勾配降下法アルゴリズムを実装するためのコード ロジック
Python を使用してミニバッチ勾配降下法アルゴリズムを実装するためのコード ロジック
- PHPz転載
- 2024-01-22 12:33:191646ブラウズ
theta = モデル パラメーター、max_iters = エポック数とします。 itr=1,2,3,...,max_iters の場合: mini_batch(X_mini,y_mini) の場合:
バッチ X_mini のフォワード パス:
1. 小さなバッチを予測します
2. パラメーターの現在の値を使用して予測誤差 (J(θ)) を計算します。
送信後: 勾配 (θ)=J(θ) を計算します。θ の偏導関数を計算します
パラメータの更新: theta=theta–learning_rate*gradient(theta)
Python で勾配降下法アルゴリズムを実装するためのコード プロセス
ステップ 1: 依存関係をインポートし、線形回帰用のデータを生成、生成されたデータを視覚化します。 8000 個のデータ例を考えます。各例には 2 つの属性特徴があります。これらのデータ サンプルはさらに、トレーニング セット (X_train、y_train) とテスト セット (X_test、y_test) に分割され、それぞれ 7200 サンプルと 800 サンプルになります。
import numpy as np import matplotlib.pyplot as plt mean=np.array([5.0,6.0]) cov=np.array([[1.0,0.95],[0.95,1.2]]) data=np.random.multivariate_normal(mean,cov,8000) plt.scatter(data[:500,0],data[:500,1],marker='.') plt.show() data=np.hstack((np.ones((data.shape[0],1)),data)) split_factor=0.90 split=int(split_factor*data.shape[0]) X_train=data[:split,:-1] y_train=data[:split,-1].reshape((-1,1)) X_test=data[split:,:-1] y_test=data[split:,-1].reshape((-1,1)) print(& quot Number of examples in training set= % d & quot % (X_train.shape[0])) print(& quot Number of examples in testing set= % d & quot % (X_test.shape[0]))
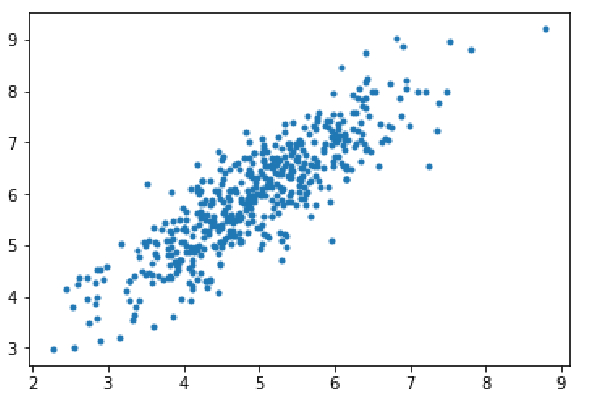
トレーニング セット内のサンプルの数 = 7200 テスト セット内のサンプルの数 = 800
ステップ 2:
mini を使用して線形回帰を実装するコード-バッチ勾配降下法。 gradientDescent() は主な駆動関数であり、他の関数は補助関数です。
Prediction-仮説()
Calculate gradient-gradient()
Calculate error- -cost ()
ミニバッチの作成 —create_mini_batches()
ドライバー関数はパラメーターを初期化し、モデルに最適なパラメーター セットを計算し、パラメーター更新エラー履歴を含むリストとともにこれらのパラメーターを返します。
def hypothesis(X,theta):
return np.dot(X,theta)
def gradient(X,y,theta):
h=hypothesis(X,theta)
grad=np.dot(X.transpose(),(h-y))
return grad
def cost(X,y,theta):
h=hypothesis(X,theta)
J=np.dot((h-y).transpose(),(h-y))
J/=2
return J[0]
def create_mini_batches(X,y,batch_size):
mini_batches=[]
data=np.hstack((X,y))
np.random.shuffle(data)
n_minibatches=data.shape[0]//batch_size
i=0
for i in range(n_minibatches+1):
mini_batch=data[i*batch_size:(i+1)*batch_size,:]
X_mini=mini_batch[:,:-1]
Y_mini=mini_batch[:,-1].reshape((-1,1))
mini_batches.append((X_mini,Y_mini))
if data.shape[0]%batch_size!=0:
mini_batch=data[i*batch_size:data.shape[0]]
X_mini=mini_batch[:,:-1]
Y_mini=mini_batch[:,-1].reshape((-1,1))
mini_batches.append((X_mini,Y_mini))
return mini_batches
def gradientDescent(X,y,learning_rate=0.001,batch_size=32):
theta=np.zeros((X.shape[1],1))
error_list=[]
max_iters=3
for itr in range(max_iters):
mini_batches=create_mini_batches(X,y,batch_size)
for mini_batch in mini_batches:
X_mini,y_mini=mini_batch
theta=theta-learning_rate*gradient(X_mini,y_mini,theta)
error_list.append(cost(X_mini,y_mini,theta))
return theta,error_listgradientDescent() 関数を呼び出してモデル パラメーター (シータ) を計算し、誤差関数の変化を視覚化します。
theta,error_list=gradientDescent(X_train,y_train)
print("Bias=",theta[0])
print("Coefficients=",theta[1:])
plt.plot(error_list)
plt.xlabel("Number of iterations")
plt.ylabel("Cost")
plt.show()Deviation=[0.81830471]Coefficient=[[1.04586595]]
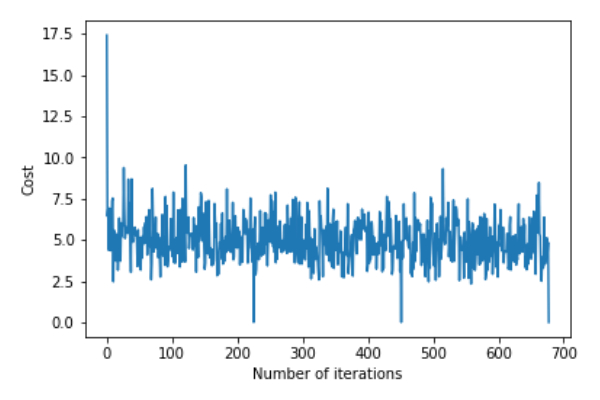
ステップ 3: テスト セットを予測し、予測における平均絶対誤差を計算します。
y_pred=hypothesis(X_test,theta) plt.scatter(X_test[:,1],y_test[:,],marker='.') plt.plot(X_test[:,1],y_pred,color='orange') plt.show() error=np.sum(np.abs(y_test-y_pred)/y_test.shape[0]) print(& quot Mean absolute error=",error)
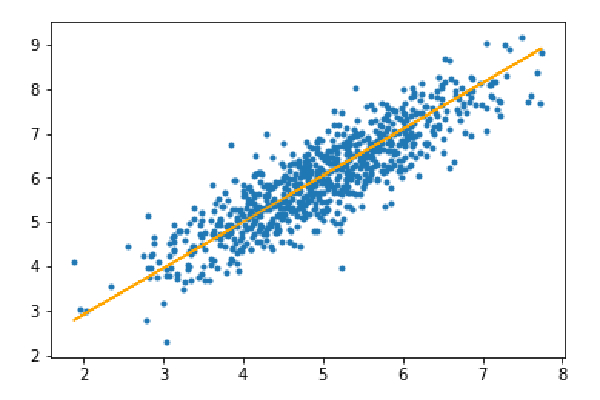
平均絶対誤差=0.4366644295854125
オレンジ色の線は、最終的な仮説関数を表します: theta[0] theta[1]*X_test[:,1] theta[2]* X_test[:,2]=0
以上がPython を使用してミニバッチ勾配降下法アルゴリズムを実装するためのコード ロジックの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

