 テクノロジー周辺機器
テクノロジー周辺機器 AI
AI Google Mathematical AI が Nature に記事を掲載: ウー・ウェンジュンの 1978 年の法則定理を超え、世界クラスの幾何学的レベルを実証
Google Mathematical AI が Nature に記事を掲載: ウー・ウェンジュンの 1978 年の法則定理を超え、世界クラスの幾何学的レベルを実証Google Mathematical AI が Nature に記事を掲載: ウー・ウェンジュンの 1978 年の法則定理を超え、世界クラスの幾何学的レベルを実証
Google DeepMind は Nature を再びリリースし、AI の Alpha シリーズが復活し、数学のレベルは飛躍的に向上しました。
AlphaGeometry、IMO 金メダル選手の幾何学的レベルに達するために人間によるデモンストレーションは必要ありません。


陈伊婷 (Evan Chen) は、AI によって生成された回答を評価する責任を負い、次のようにコメントしました。
##AlphaGeometry の出力は、信頼性が高く、クリーンであり、印象的です。これまでの AI ソリューションは当たり外れが多く、結果として手動でのレビューが必要になる場合もありました。AlphaGeometry のソリューションは、マシンによって検証でき、人間によって理解できる検証可能な構造を備えています。学生と同じように、角度や類似の三角形などの古典的な幾何学ルールを使用します。
優れた結果に加えて、この研究には業界の注目を集めている 3 つの重要なポイントがあります。
- 必要ありません。人間によるデモンストレーション、つまり、AlphaZero の自己学習 Go メソッドを継続して、AI 合成データ トレーニングのみが使用されます。
- 他の AI 手法と組み合わせた大規模モデル、AlphaGo や OpenAI Q* の噂に似ています。 これまでの多くの方法とは異なり、AlphaGeometry は人間が読める証明を生成でき、モデルとコードは両方ともオープンソースです。
 #チームは、AlphaGeometry が高度な推論能力を実現し、新しい知識を発見するための潜在的なフレームワークを提供すると信じています。
#チームは、AlphaGeometry が高度な推論能力を実現し、新しい知識を発見するための潜在的なフレームワークを提供すると信じています。
 さらに、著者のチームとのコミュニケーションプロセス中に、Qubits は、AlphaGo チャレンジと同様に、AlphaGeometry が本当に IMO 競技会に参加することを許可されるかどうかを尋ねました。人間の囲碁チャンピオンのように。
さらに、著者のチームとのコミュニケーションプロセス中に、Qubits は、AlphaGo チャレンジと同様に、AlphaGeometry が本当に IMO 競技会に参加することを許可されるかどうかを尋ねました。人間の囲碁チャンピオンのように。
彼らは、システムの機能を向上させるために熱心に取り組んでおり、AI が幾何学を超えた幅広い数学的問題を解決できるようにする必要があると述べました。
AI は幾何学も補助線を引くことを証明しました
以前、AI システムは幾何学的な問題をうまく解決できず、高品質のトレーニング データが不足していたため行き詰まっていました。
幾何学を学習している人間は、紙とペンを使って画像に関する既存の知識を利用して、新しくより複雑な幾何学的特性と関係を発見できます。
Google チームは、この目的のために 10 億のランダムな幾何学的オブジェクト グラフと、それらの点と線の間のすべての関係を生成し、最終的に 1 億の固有の定理とさまざまな困難の証明を選別しました。これらのデータを最初からトレーニングします。
 システムは、複雑な幾何学的証明を見つけるために相互に連携する 2 つのモジュールで構成されています。
システムは、複雑な幾何学的証明を見つけるために相互に連携する 2 つのモジュールで構成されています。
- 言語モデル、問題を解決するために使用できる幾何学的構造 を予測します (つまり、補助線を追加します) 。
- 記号推論エンジン、論理ルールを使用して結論を導き出します。
 筆頭著者 Trieu Trinh は、AlphaGeometry の演算プロセスは人間の脳が速いタイプと遅いタイプに分けられるのと似ていると紹介しました。
筆頭著者 Trieu Trinh は、AlphaGeometry の演算プロセスは人間の脳が速いタイプと遅いタイプに分けられるのと似ていると紹介しました。
これは、ノーベル賞受賞者ダニエル・カーネマンのベストセラー本「Thinking Fast and Slow」で広められた「システム 1、システム 2」の概念です。
システム 1 は迅速で直感的なアイデアを提供し、システム 2 はより思慮深く合理的な決定を提供します。
一方で、言語モデルはデータ内のパターンと関係を識別するのが得意で、潜在的に有用な補助構造を迅速に予測できますが、多くの場合、その決定を厳密に推論したり説明したりする能力が欠けています。
一方、記号推論エンジンは形式論理に基づいており、明示的なルールを使用して結論を導き出します。これらは合理的で説明可能ですが、特に大規模で複雑な問題を単独で処理する場合、時間がかかり、柔軟性に欠けます。
たとえば、IMO 2015 のコンテストの問題を解く場合、青い部分は AlphaGeometry の言語モデルによって追加された補助構造、緑色の部分は最終証明の簡易バージョンで、合計 109 のステップがあります。

この問題を解決する過程で、AlphaGeometry は 2004 年の IMO コンテストの問題で未使用の前提条件も発見し、定理のより広範なバージョンを発見しました。
O が BC の中点であるという条件なしで、P、B、および C が同一線上にあることを証明できます。

さらに、この研究では、人間のスコアが最も低い 3 つの問題についても、AlphaGeometry では非常に長い証明プロセスと多くの追加が必要であることも判明しました。解決する補助構造の。
しかし、比較的簡単な問題では、人間の平均スコアと AI によって生成された証明の長さとの間に有意な相関はありませんでした (p = −0.06)。

もう 1 つ
AlphaGeometry と AlphaGo の関係と違いについて、チームとのコミュニケーションの過程で、Google の科学者が Quoc Le はじめに:
これらはすべて非常に複雑な意思決定空間で検索しますが、AlphaGo の方法はより伝統的です(注: ニューラル ネットワークはパターン認識を担当します), AlphaGeometry のニューラル ネットワークは、次にとるべきアクションを提案し、決定空間内で正しい方向に進むように検索アルゴリズムを誘導する責任があります。
この結果は Alpha シリーズにちなんで名付けられており、最初のユニットも Google DeepMind ですが、著者は実際には元 Google Brain メンバーです。
Quoc Le マスターについては説明の必要はありません。筆頭著者の Trieu Trinh 氏と責任著者の Thang Luong 氏は、どちらも Google で 6 ~ 7 年間働いています。Thang Luong 氏自身も高校時代は IMO プレーヤーでした。
二人の中国人作家のうち、何何さんはニューヨーク大学の助教授です。 Wu Yuhuai 氏は以前、Google の大規模数学モデル Minerva の研究に参加していましたが、現在は Google を辞めてマスク氏のチームに加わり、xAI の共同創設者の 1 人になっています。
論文アドレス: https://www.nature.com/articles/s41586-023-06747-5。
参考リンク:
[1]https://www.nature.com/articles/d4186-024-00141 -5.
[2]https://deepmind.google/discover/blog/alphageometry-an-olympiad-level-ai-system-for-geometry。
以上がGoogle Mathematical AI が Nature に記事を掲載: ウー・ウェンジュンの 1978 年の法則定理を超え、世界クラスの幾何学的レベルを実証の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 踊りましょう:私たちの人間のニューラルネットを微調整するための構造化された動きApr 27, 2025 am 11:09 AM
踊りましょう:私たちの人間のニューラルネットを微調整するための構造化された動きApr 27, 2025 am 11:09 AM科学者は、彼らの機能を理解するために、人間とより単純なニューラルネットワーク(C. elegansのものと同様)を広く研究してきました。 ただし、重要な疑問が生じます。新しいAIと一緒に効果的に作業するために独自のニューラルネットワークをどのように適応させるのか
 新しいGoogleリークは、Gemini AIのサブスクリプションの変更を明らかにしますApr 27, 2025 am 11:08 AM
新しいGoogleリークは、Gemini AIのサブスクリプションの変更を明らかにしますApr 27, 2025 am 11:08 AMGoogleのGemini Advanced:Horizonの新しいサブスクリプションティア 現在、Gemini Advancedにアクセスするには、1か月あたり19.99ドルのGoogle One AIプレミアムプランが必要です。 ただし、Android Authorityのレポートは、今後の変更を示唆しています。 最新のGoogle p
 データ分析の加速がAIの隠されたボトルネックをどのように解決しているかApr 27, 2025 am 11:07 AM
データ分析の加速がAIの隠されたボトルネックをどのように解決しているかApr 27, 2025 am 11:07 AM高度なAI機能を取り巻く誇大宣伝にもかかわらず、エンタープライズAIの展開内に大きな課題が潜んでいます:データ処理ボトルネック。 CEOがAIの進歩を祝う間、エンジニアはクエリの遅い時間、過負荷のパイプライン、
 MarkitDown MCPは、任意のドキュメントをマークダウンに変換できます!Apr 27, 2025 am 09:47 AM
MarkitDown MCPは、任意のドキュメントをマークダウンに変換できます!Apr 27, 2025 am 09:47 AMドキュメントの取り扱いは、AIプロジェクトでファイルを開くだけでなく、カオスを明確に変えることです。 PDF、PowerPoint、Wordなどのドキュメントは、あらゆる形状とサイズでワークフローをフラッシュします。構造化された取得
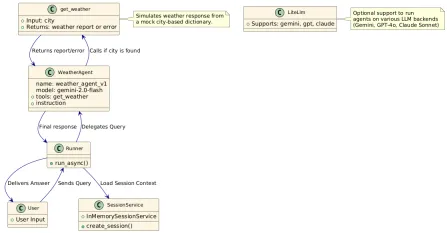 建物のエージェントにGoogle ADKを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:42 AM
建物のエージェントにGoogle ADKを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:42 AMGoogleのエージェント開発キット(ADK)のパワーを活用して、実際の機能を備えたインテリジェントエージェントを作成します。このチュートリアルは、ADKを使用して会話エージェントを構築し、GeminiやGPTなどのさまざまな言語モデルをサポートすることをガイドします。 w
 効果的な問題解決のためにLLMを介したSLMの使用 - 分析VidhyaApr 27, 2025 am 09:27 AM
効果的な問題解決のためにLLMを介したSLMの使用 - 分析VidhyaApr 27, 2025 am 09:27 AMまとめ: Small Language Model(SLM)は、効率のために設計されています。それらは、リソース不足、リアルタイム、プライバシーに敏感な環境の大手言語モデル(LLM)よりも優れています。 特にドメインの特異性、制御可能性、解釈可能性が一般的な知識や創造性よりも重要である場合、フォーカスベースのタスクに最適です。 SLMはLLMSの代替品ではありませんが、精度、速度、費用対効果が重要な場合に理想的です。 テクノロジーは、より少ないリソースでより多くを達成するのに役立ちます。それは常にドライバーではなく、プロモーターでした。蒸気エンジンの時代からインターネットバブル時代まで、テクノロジーの力は、問題の解決に役立つ範囲にあります。人工知能(AI)および最近では生成AIも例外ではありません
 コンピュータービジョンタスクにGoogle Geminiモデルを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:26 AM
コンピュータービジョンタスクにGoogle Geminiモデルを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:26 AMコンピュータービジョンのためのGoogleGeminiの力を活用:包括的なガイド 大手AIチャットボットであるGoogle Geminiは、その機能を会話を超えて拡張して、強力なコンピュータービジョン機能を網羅しています。 このガイドの利用方法については、
 Gemini 2.0 Flash vs O4-Mini:GoogleはOpenaiよりもうまくやることができますか?Apr 27, 2025 am 09:20 AM
Gemini 2.0 Flash vs O4-Mini:GoogleはOpenaiよりもうまくやることができますか?Apr 27, 2025 am 09:20 AM2025年のAIランドスケープは、GoogleのGemini 2.0 FlashとOpenaiのO4-Miniの到着とともに感動的です。 数週間離れたこれらの最先端のモデルは、同等の高度な機能と印象的なベンチマークスコアを誇っています。この詳細な比較


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

PhpStorm Mac バージョン
最新(2018.2.1)のプロフェッショナル向けPHP統合開発ツール

ZendStudio 13.5.1 Mac
強力な PHP 統合開発環境

DVWA
Damn Vulnerable Web App (DVWA) は、非常に脆弱な PHP/MySQL Web アプリケーションです。その主な目的は、セキュリティ専門家が法的環境でスキルとツールをテストするのに役立ち、Web 開発者が Web アプリケーションを保護するプロセスをより深く理解できるようにし、教師/生徒が教室環境で Web アプリケーションを教え/学習できるようにすることです。安全。 DVWA の目標は、シンプルでわかりやすいインターフェイスを通じて、さまざまな難易度で最も一般的な Web 脆弱性のいくつかを実践することです。このソフトウェアは、

AtomエディタMac版ダウンロード
最も人気のあるオープンソースエディター

メモ帳++7.3.1
使いやすく無料のコードエディター

ホットトピック
 7770
7770 15
15 1644
1644 14
14 1399
1399 52
52 1296
1296 25
25 1234
1234 29
29


