ホームページ >テクノロジー周辺機器 >AI >PyTorchを使用したノイズ除去拡散モデルの実装
PyTorchを使用したノイズ除去拡散モデルの実装
- 王林転載
- 2024-01-14 22:33:431058ブラウズ
ノイズ除去拡散確率モデル (DDPM) の動作原理を詳しく理解する前に、まず、DDPM の基礎研究の 1 つである生成人工知能の開発の一部を理解しましょう。

VAE
VAE は、エンコーダー、確率的潜在空間、およびデコーダーを使用します。トレーニング中に、エンコーダーは各画像の平均と分散を予測し、ガウス分布からこれらの値をサンプリングします。サンプリングの結果はデコーダに渡され、入力画像が出力画像と同様の形式に変換されます。 KL ダイバージェンスは損失の計算に使用されます。 VAE の大きな利点は、多様な画像を生成できることです。サンプリング段階では、ガウス分布から直接サンプリングし、デコーダを通じて新しい画像を生成できます。
GAN
変分オートエンコーダ (VAE) からわずか 1 年で、画期的な生成モデル ファミリが登場しました。 — 敵対的生成ネットワーク (GAN) ) これは、敵対的なトレーニング プロセスを伴う、ジェネレーターとディスクリミネーターという 2 つのニューラル ネットワークの連携を特徴とする、新しいクラスの生成モデルの始まりを示しています。ジェネレーターの目的は、ランダム ノイズから画像などの実際のデータを生成することですが、ディスクリミネーターは、生成されたデータから実際のデータを区別することに努めます。トレーニング段階を通じて、ジェネレーターとディスクリミネーターは、競争的な学習プロセスを通じて能力を継続的に向上させます。ジェネレーターはますます説得力のあるデータを生成するため、ディスクリミネーターよりも賢くなり、実際のサンプルと生成されたサンプルを区別する能力が向上します。この敵対的な相互作用により、ジェネレーターは高品質で現実的なデータを生成します。 GAN トレーニング後のサンプリング段階では、ジェネレーターがランダム ノイズを入力して新しいサンプルを生成します。このノイズを、一般に実際の例を反映するデータに変換します。
別のモデル アーキテクチャが必要な理由
GAN と VAE には画像生成においてそれぞれ利点がありますが、両方ともいくつかの問題があります。 GAN はトレーニング セット内の画像によく似たリアルな画像を生成できますが、生成された結果には多様性がありません。 VAE はさまざまな画像を作成できますが、ぼやけた画像が生成される傾向があります。 しかし、これら 2 つの機能を組み合わせて、非常に現実的で多様な画像を作成することには成功していません。この課題は研究者にとって重大な障害となっており、対処する必要があります。したがって、将来の研究の方向性の 1 つは、GAN と VAE の利点を組み合わせて、非常に現実的で多様な画像生成を実現する方法を探ることです。これは画像生成の分野に大きな進歩をもたらし、さまざまな分野で広く使用されることになります。
GAN 論文の発表から 6 年後、VAE 論文の発表から 7 年後、ノイズ除去拡散確率モデル (DDPM) という画期的なモデルが登場しました。 DDPM は両方の分野の利点を組み合わせて、多様でリアルな画像を作成します。
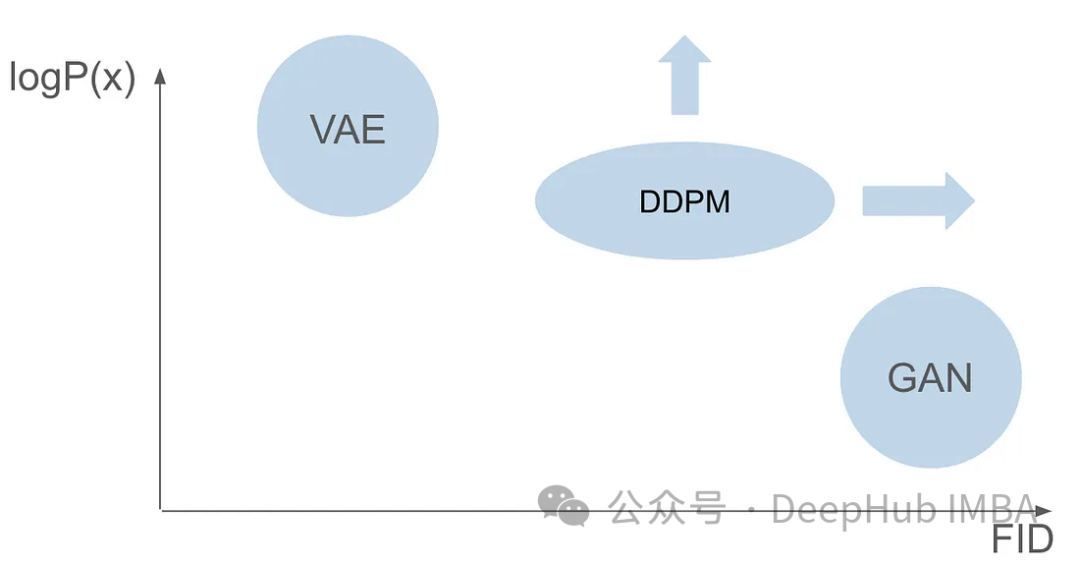
#この記事では、トレーニング プロセス、フォワード プロセスとリバース プロセス、サンプリング方法など、DDPM の複雑さについて詳しく説明します。 PyTorch を使用して DDPM を最初から構築してトレーニングし、プロセス全体を読者にガイドします。
読者はディープ ラーニングの基本知識をすでに理解しており、ディープ コンピューター ビジョンのしっかりした基礎を持っていることを前提としています。これらの基本概念については詳しく説明しませんが、その代わりに、信頼できる画像を生成することを目指します。
DDPM
ノイズ除去拡散確率モデル (DDPM) は、生成モデルの分野における最先端の手法です。明示的な尤度関数に依存する従来のモデルと比較して、DDPM は反復的なノイズ除去拡散プロセスを通じて動作します。このプロセスでは、画像にノイズを徐々に追加し、そのノイズを除去しようとします。基本理論は、一連の拡散ステップを通じて、単純な分布 (ガウス分布など) を複雑で表現力豊かな画像データ分布に変換するという考えに基づいています。言い換えれば、サンプルを元の画像分布からガウス分布に移すことによって、このプロセスを逆にするモデルを構築できます。これにより、完全なガウス分布から開始して画像分布特性を備えた新しい画像を生成できるため、効率的な画像生成が実現します。
DDPM のトレーニングは 2 つの基本的なステップで構成されます。1 つは固定され学習できないノイズの多い画像を生成する順方向プロセス、もう 1 つはその後の逆方向プロセスです。逆プロセスの主な目的は、特殊な機械学習モデルを使用して画像のノイズを除去することです。
前方拡散プロセス
前方プロセスは固定された学習不可能なステップですが、いくつかの事前定義された設定が必要です。設定に入る前に、まずそれがどのように機能するかを理解しましょう。
このプロセスの核となるコンセプトは、明確なイメージから始めることです。 「T」で示される特定のステップ サイズでは、ガウス分布に従って少量のノイズが徐々に導入されます。

画像からわかるように、ステップごとにノイズが増加しています。このノイズの数学的表現を詳しく見てみましょう。
ノイズはガウス分布からサンプリングされます。各ステップで少量のノイズを導入するために、マルコフ連鎖を使用します。現在のタイムスタンプのイメージを生成するには、最後のタイムスタンプのイメージのみが必要です。マルコフ連鎖の概念がここで重要であり、その後の数学的詳細にとって非常に重要になります。
マルコフ連鎖は確率過程であり、特定の状態への遷移確率は、前の一連のイベントには依存せず、現在の状態と経過時間のみに依存します。この機能により、ノイズ追加プロセスのモデリングが簡素化され、数学的な分析が容易になります。
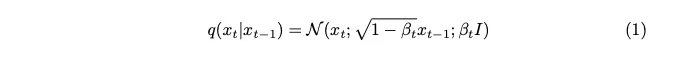
ベータとして表される分散パラメーターは、各ステップ ノイズで最小限の量のみを導入するために、意図的に非常に小さな値に設定されています。
ステップ パラメーター「T」は、完全にノイズのある画像を生成するために必要なステップ サイズを決定します。この記事では、このパラメータは 1000 に設定されていますが、これは大きく見えるかもしれません。データセット内の元の画像ごとに 1000 個のノイズの多い画像を作成する必要があるのでしょうか? マルコフ連鎖の側面がこの問題の解決に役立つことが証明されています。次のステップを予測するには前のステップの画像のみが必要であり、各ステップで追加されるノイズは同じままであるため、特定のタイムスタンプでノイズのある画像を生成することで計算を簡素化できます。ペアの再パラメータ化手法を採用すると、方程式をさらに簡素化できます。
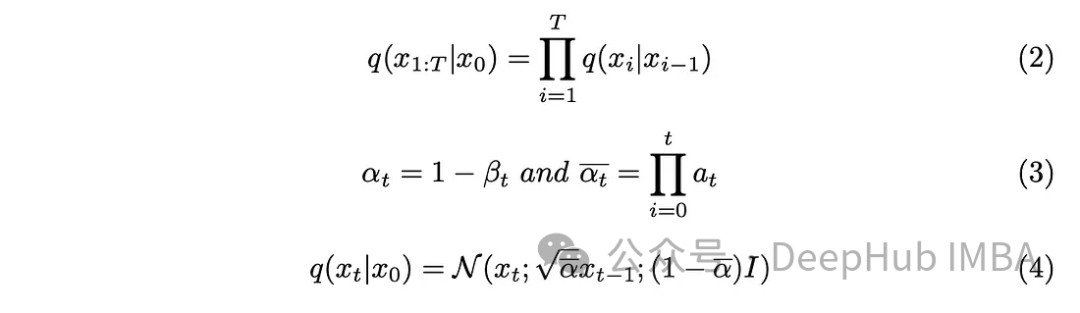
式 (3) で導入された新しいパラメーターを式 (2) に組み込み、式 (2) を展開し、結果を取得します。
逆拡散プロセス
画像にノイズを導入しました。次のステップは、逆演算を実行することです。初期条件、つまり t = 0 でのノイズ除去されていない画像が分からない限り、逆のプロセスを数学的に実装して画像のノイズを除去することは不可能です。私たちの目標は、ノイズから直接サンプリングして新しい画像を作成することですが、ここでは結果に関する情報が不足しています。したがって、結果を知ることなく画像から段階的にノイズを除去する方法を考案する必要があります。そこで、この複雑な数学関数を近似するために深層学習モデルを使用するという解決策が生まれました。
少し数学的な背景を踏まえると、モデルは式 (5) を近似します。注目に値する詳細の 1 つは、モデルに分散を学習させることも可能ですが、元の DDPM 論文にこだわり、分散を固定することです。
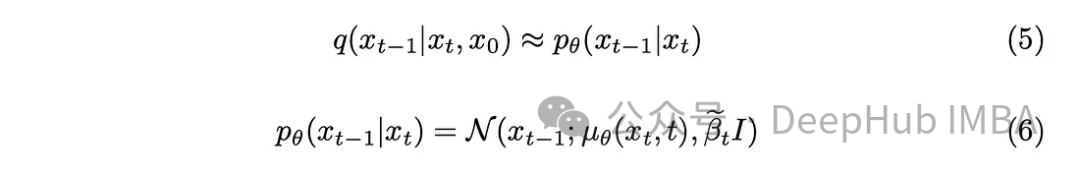
モデルは、現在のタイムスタンプと前のタイムスタンプの間に追加されたノイズの平均を予測する役割を果たします。これにより、ノイズを効果的に除去し、望ましい効果を得ることができます。しかし、私たちの目標が、「元の画像」から最後のタイムスタンプに追加されるノイズをモデルに予測させることである場合はどうなるでしょうか?
ノイズのない最初の画像が分からない限り、それは数学的に不可能です。逆のプロセスは難しいので、事後分散を定義することから始めましょう。

#モデルのタスクは、タイムスタンプ t で画像に追加されるノイズを最初の画像から予測することです。順方向プロセスを使用すると、鮮明な画像から開始して、タイムスタンプ t でノイズの多い画像に進むこの操作を実行できます。
トレーニング アルゴリズム
予測を行うために使用されるモデル アーキテクチャは U-Net であると仮定します。トレーニング フェーズの目標は、データセット内の各画像に対して、範囲 [0, T] のタイムスタンプをランダムに選択し、前方拡散プロセスを計算することです。これにより、使用される実際のノイズと同様に、クリアで多少ノイズの多い画像が生成されます。次に、このモデルを使用して、逆プロセスの理解を使用して画像に追加されるノイズを予測します。実際のノイズと予測されたノイズにより、教師あり機械学習の問題に入ったようです。
最も重要な問題は、モデルをトレーニングするためにどの損失関数を使用すべきかということです? 確率的潜在空間を扱っているため、カルバック-ライブラー (KL) 発散が適切です。選択。
KL 発散は、2 つの確率分布 (この場合、モデルによって予測された分布と予想される分布) 間の差を測定します。 KL 発散を損失関数に組み込むと、モデルが正確な予測を生成するようになるだけでなく、潜在空間表現が目的の確率構造に確実に適合するようになります。
KL 発散は L2 損失関数として近似できるため、次の損失関数を取得できます。
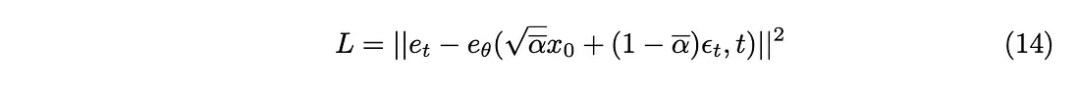
## 最後に、論文で提案されているトレーニング アルゴリズムを入手しました。

サンプリング
逆のプロセスについては説明しました。ここではその使用方法を説明します。時間 T の完全にランダムな画像から開始し、逆のプロセスを T 回使用して、最終的に時間 0 に到達します。これは、この記事で概説する 2 番目のアルゴリズムを形成します。

パラメータ
さまざまなパラメータのベータ版が用意されています。 beta_tildes、alpha、alpha_hat など。これらのパラメータを選択する方法がまだわかりません。ただし、この時点でわかっているパラメータは T だけであり、1000 に設定されています。
リストされているすべてのパラメータについて、その選択はベータ版によって異なります。ある意味、ベータは各ステップで追加するノイズの量を決定します。したがって、アルゴリズムを確実に成功させるには、慎重なベータ選択が重要です。他にもパラメータが多すぎるので論文を参照してください。
元の論文の実験段階では、さまざまなサンプリング方法が検討されました。元の線形サンプリング方式の画像は、ノイズが不十分か、ノイズが多すぎるかのいずれかでした。この問題を解決するために、コサイン サンプリングという別のより一般的な方法が採用されています。コサイン サンプリングにより、よりスムーズで一貫したノイズの追加が可能になります。
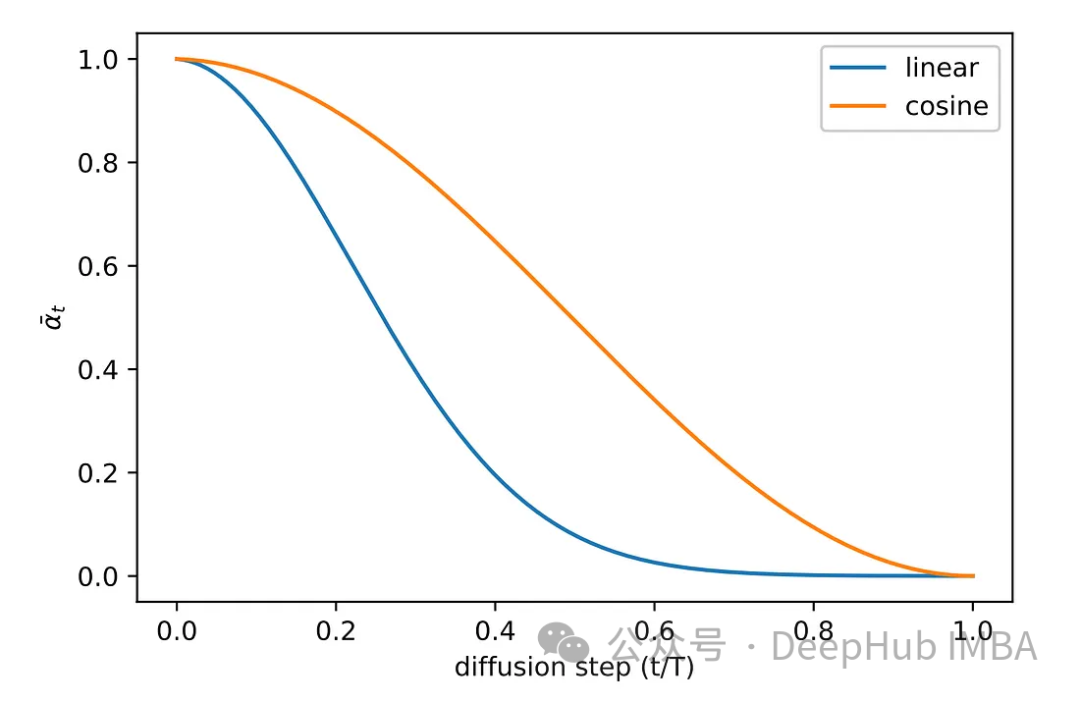
Pytorch 実装のモデル
ノイズ予測に U-Net アーキテクチャを使用します。その理由は次のとおりです。 U-Net は、空間マップと特徴マップをキャプチャし、入力と同じ出力サイズを提供する画像処理に理想的なアーキテクチャであるため、U-Net を選択するのに最適です。
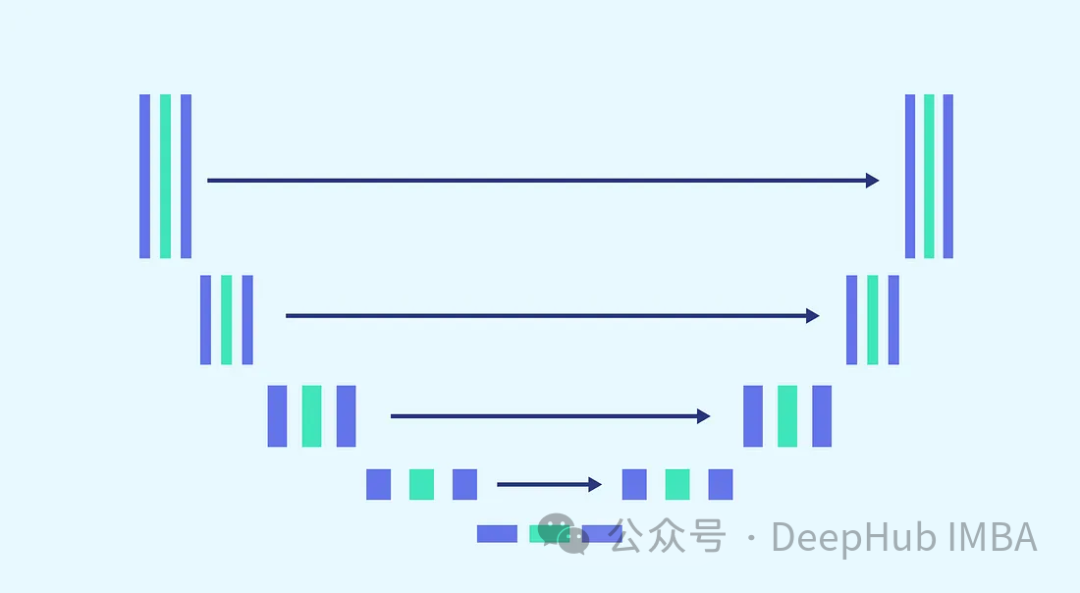
タスクの複雑さと、各ステップで同じモデルを使用するという要件 (モデルがノイズを除去できる必要がある場合) を考慮します。完全にノイズのある画像とわずかにノイズのある画像と同じ重みを持つ)、モデルの調整が不可欠です。これには、より複雑なブロックのマージや、正弦波埋め込みステップを介して使用されるタイムスタンプの認識の導入が含まれます。これらの機能強化の目的は、モデルをノイズ除去タスクのエキスパートにすることです。完全なモデルの構築に進む前に、各ブロックを紹介します。
ConvNext ブロック
モデルの複雑性を高めるニーズを満たすために、畳み込みブロックは重要な役割を果たします。ここでは、u-net ペーパーの基本ブロックにのみ依存することはできません。これを ConvNext と組み合わせます。
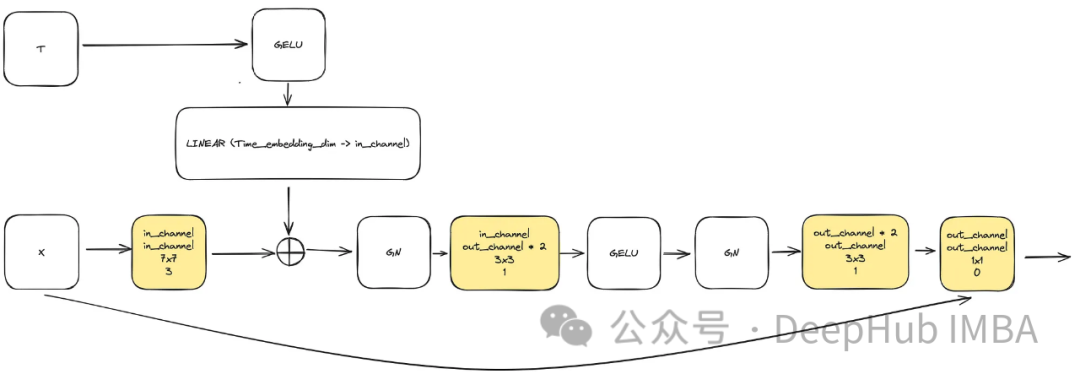
入力は、画像を表す「x」と、サイズ「time_embedding_dim」の埋め込みタイムスタンプ視覚化「t」で構成されます。プロセス全体を通じて、ブロックはその複雑さと入力層と最終層への残りの接続により、空間マップと特徴マップの学習において重要な役割を果たします。
class ConvNextBlock(nn.Module):def __init__(self,in_channels,out_channels,mult=2,time_embedding_dim=None,norm=True,group=8,):super().__init__()self.mlp = (nn.Sequential(nn.GELU(), nn.Linear(time_embedding_dim, in_channels))if time_embedding_dimelse None) self.in_conv = nn.Conv2d(in_channels, in_channels, 7, padding=3, groups=in_channels) self.block = nn.Sequential(nn.GroupNorm(1, in_channels) if norm else nn.Identity(),nn.Conv2d(in_channels, out_channels * mult, 3, padding=1),nn.GELU(),nn.GroupNorm(1, out_channels * mult),nn.Conv2d(out_channels * mult, out_channels, 3, padding=1),) self.residual_conv = (nn.Conv2d(in_channels, out_channels, 1)if in_channels != out_channelselse nn.Identity()) def forward(self, x, time_embedding=None):h = self.in_conv(x)if self.mlp is not None and time_embedding is not None:assert self.mlp is not None, "MLP is None"h = h + rearrange(self.mlp(time_embedding), "b c -> b c 1 1")h = self.block(h)return h + self.residual_conv(x)
正弦波タイムスタンプの埋め込み
モデル内の重要なブロックの 1 つは、正弦波タイムスタンプの埋め込みブロックです。これにより、エンコードが可能になります。モデルはすべての異なるタイムスタンプに使用されるため、モデルのデコードに必要な現在時間に関する情報を保持します。
これは非常に古典的な実装であり、さまざまな場所で使用されています。コードを直接貼り付けます
class SinusoidalPosEmb(nn.Module):def __init__(self, dim, theta=10000):super().__init__()self.dim = dimself.theta = theta def forward(self, x):device = x.devicehalf_dim = self.dim // 2emb = math.log(self.theta) / (half_dim - 1)emb = torch.exp(torch.arange(half_dim, device=device) * -emb)emb = x[:, None] * emb[None, :]emb = torch.cat((emb.sin(), emb.cos()), dim=-1)return emb
DownSample & UpSample
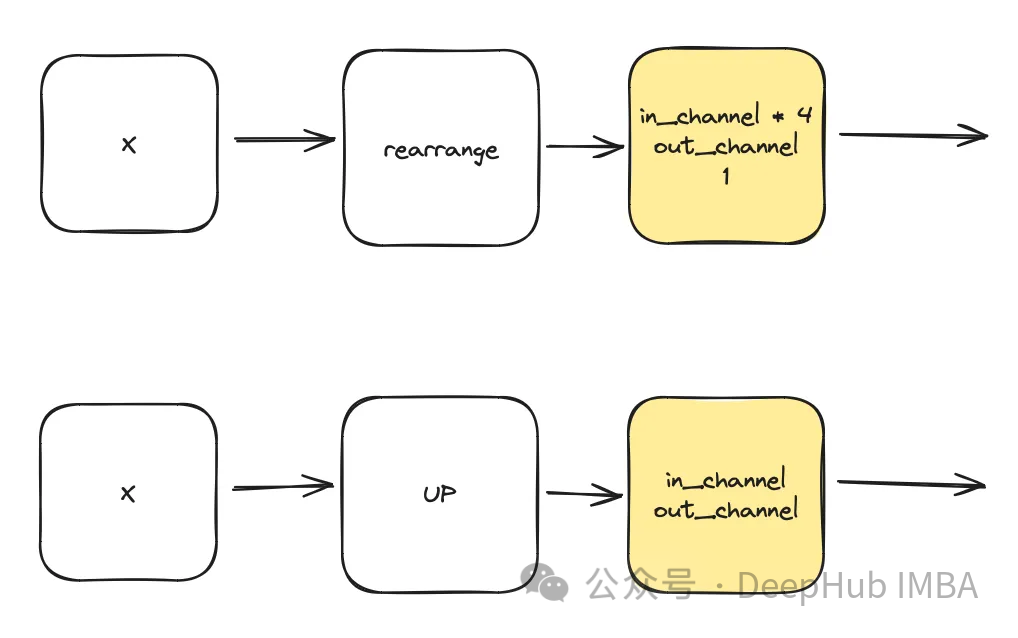
class DownSample(nn.Module):def __init__(self, dim, dim_out=None):super().__init__()self.net = nn.Sequential(Rearrange("b c (h p1) (w p2) -> b (c p1 p2) h w", p1=2, p2=2),nn.Conv2d(dim * 4, default(dim_out, dim), 1),) def forward(self, x):return self.net(x) class Upsample(nn.Module):def __init__(self, dim, dim_out=None):super().__init__()self.net = nn.Sequential(nn.Upsample(scale_factor=2, mode="nearest"),nn.Conv2d(dim, dim_out or dim, kernel_size=3, padding=1),) def forward(self, x):return self.net(x)
時間多層パーセプトロン
このモジュールは、それを利用して、指定されたタイムスタンプ t に基づいて時間を計算します。作成時の表現。この多層パーセプトロン (MLP) の出力は、変更されたすべての ConvNext ブロックへの入力 "t" としても機能します。

ここで、「dim」はモデルのハイパーパラメータで、最初のブロックに必要なチャネル数を示します。これは、後続のブロックのチャネル数の基本計算として機能します。
sinu_pos_emb = SinusoidalPosEmb(dim, theta=10000) time_dim = dim * 4 time_mlp = nn.Sequential(sinu_pos_emb,nn.Linear(dim, time_dim),nn.GELU(),nn.Linear(time_dim, time_dim),)
注意
これは、unet で使用されるオプションのコンポーネントです。注意力は、学習における残りのつながりの役割を強化するのに役立ちます。それは、残差接続によって計算された注意メカニズムと中および低潜在空間によって計算された特徴マップを通じて、Unet の左側から得られた重要な空間情報にさらに注意を払います。これは ACC-UNet 論文からのものです。
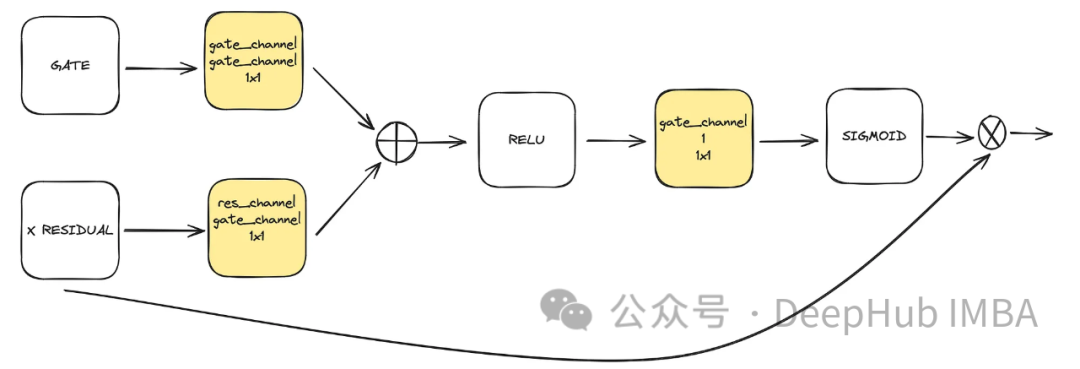
#gate は下位ブロックのアップサンプリングされた出力を表し、x-residual はアテンションが適用されるレベルでの残差接続を表します。
class BlockAttention(nn.Module):def __init__(self, gate_in_channel, residual_in_channel, scale_factor):super().__init__()self.gate_conv = nn.Conv2d(gate_in_channel, gate_in_channel, kernel_size=1, stride=1)self.residual_conv = nn.Conv2d(residual_in_channel, gate_in_channel, kernel_size=1, stride=1)self.in_conv = nn.Conv2d(gate_in_channel, 1, kernel_size=1, stride=1)self.relu = nn.ReLU()self.sigmoid = nn.Sigmoid() def forward(self, x: torch.Tensor, g: torch.Tensor) -> torch.Tensor:in_attention = self.relu(self.gate_conv(g) + self.residual_conv(x))in_attention = self.in_conv(in_attention)in_attention = self.sigmoid(in_attention)return in_attention * x
最后整合
将前面讨论的所有块(不包括注意力块)整合到一个Unet中。每个块都包含两个残差连接,而不是一个。这个修改是为了解决潜在的过度拟合问题。
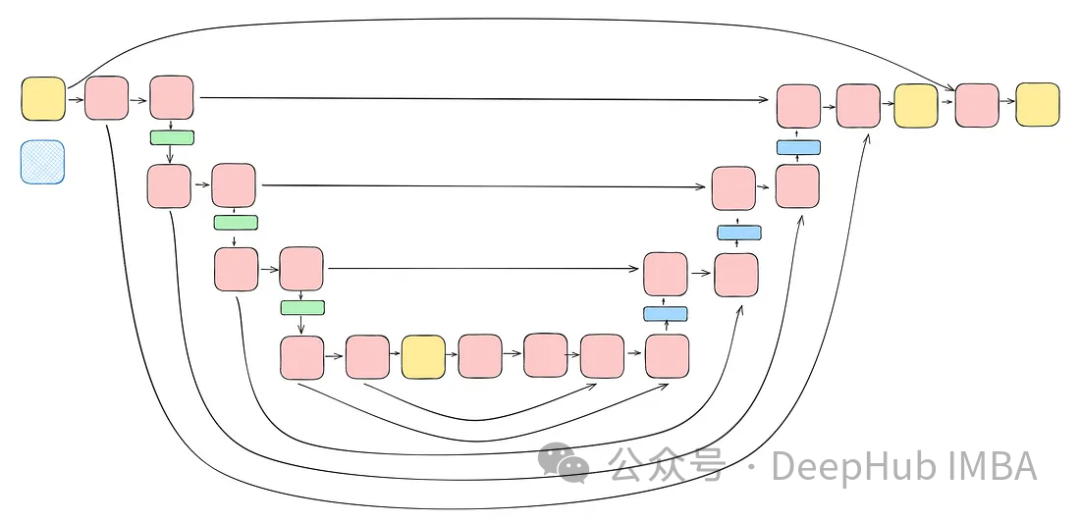
class TwoResUNet(nn.Module):def __init__(self,dim,init_dim=None,out_dim=None,dim_mults=(1, 2, 4, 8),channels=3,sinusoidal_pos_emb_theta=10000,convnext_block_groups=8,):super().__init__()self.channels = channelsinput_channels = channelsself.init_dim = default(init_dim, dim)self.init_conv = nn.Conv2d(input_channels, self.init_dim, 7, padding=3) dims = [self.init_dim, *map(lambda m: dim * m, dim_mults)]in_out = list(zip(dims[:-1], dims[1:])) sinu_pos_emb = SinusoidalPosEmb(dim, theta=sinusoidal_pos_emb_theta) time_dim = dim * 4 self.time_mlp = nn.Sequential(sinu_pos_emb,nn.Linear(dim, time_dim),nn.GELU(),nn.Linear(time_dim, time_dim),) self.downs = nn.ModuleList([])self.ups = nn.ModuleList([])num_resolutions = len(in_out) for ind, (dim_in, dim_out) in enumerate(in_out):is_last = ind >= (num_resolutions - 1) self.downs.append(nn.ModuleList([ConvNextBlock(in_channels=dim_in,out_channels=dim_in,time_embedding_dim=time_dim,group=convnext_block_groups,),ConvNextBlock(in_channels=dim_in,out_channels=dim_in,time_embedding_dim=time_dim,group=convnext_block_groups,),DownSample(dim_in, dim_out)if not is_lastelse nn.Conv2d(dim_in, dim_out, 3, padding=1),])) mid_dim = dims[-1]self.mid_block1 = ConvNextBlock(mid_dim, mid_dim, time_embedding_dim=time_dim)self.mid_block2 = ConvNextBlock(mid_dim, mid_dim, time_embedding_dim=time_dim) for ind, (dim_in, dim_out) in enumerate(reversed(in_out)):is_last = ind == (len(in_out) - 1)is_first = ind == 0 self.ups.append(nn.ModuleList([ConvNextBlock(in_channels=dim_out + dim_in,out_channels=dim_out,time_embedding_dim=time_dim,group=convnext_block_groups,),ConvNextBlock(in_channels=dim_out + dim_in,out_channels=dim_out,time_embedding_dim=time_dim,group=convnext_block_groups,),Upsample(dim_out, dim_in)if not is_lastelse nn.Conv2d(dim_out, dim_in, 3, padding=1)])) default_out_dim = channelsself.out_dim = default(out_dim, default_out_dim) self.final_res_block = ConvNextBlock(dim * 2, dim, time_embedding_dim=time_dim)self.final_conv = nn.Conv2d(dim, self.out_dim, 1) def forward(self, x, time):b, _, h, w = x.shapex = self.init_conv(x)r = x.clone() t = self.time_mlp(time) unet_stack = []for down1, down2, downsample in self.downs:x = down1(x, t)unet_stack.append(x)x = down2(x, t)unet_stack.append(x)x = downsample(x) x = self.mid_block1(x, t)x = self.mid_block2(x, t) for up1, up2, upsample in self.ups:x = torch.cat((x, unet_stack.pop()), dim=1)x = up1(x, t)x = torch.cat((x, unet_stack.pop()), dim=1)x = up2(x, t)x = upsample(x) x = torch.cat((x, r), dim=1)x = self.final_res_block(x, t) return self.final_conv(x)
扩散的代码实现
最后我们介绍一下扩散是如何实现的。由于我们已经介绍了用于正向、逆向和采样过程的所有数学理论,所里这里将重点介绍代码。
class DiffusionModel(nn.Module):SCHEDULER_MAPPING = {"linear": linear_beta_schedule,"cosine": cosine_beta_schedule,"sigmoid": sigmoid_beta_schedule,} def __init__(self,model: nn.Module,image_size: int,*,beta_scheduler: str = "linear",timesteps: int = 1000,schedule_fn_kwargs: dict | None = None,auto_normalize: bool = True,) -> None:super().__init__()self.model = model self.channels = self.model.channelsself.image_size = image_size self.beta_scheduler_fn = self.SCHEDULER_MAPPING.get(beta_scheduler)if self.beta_scheduler_fn is None:raise ValueError(f"unknown beta schedule {beta_scheduler}") if schedule_fn_kwargs is None:schedule_fn_kwargs = {} betas = self.beta_scheduler_fn(timesteps, **schedule_fn_kwargs)alphas = 1.0 - betasalphas_cumprod = torch.cumprod(alphas, dim=0)alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)posterior_variance = (betas * (1.0 - alphas_cumprod_prev) / (1.0 - alphas_cumprod)) register_buffer = lambda name, val: self.register_buffer(name, val.to(torch.float32)) register_buffer("betas", betas)register_buffer("alphas_cumprod", alphas_cumprod)register_buffer("alphas_cumprod_prev", alphas_cumprod_prev)register_buffer("sqrt_recip_alphas", torch.sqrt(1.0 / alphas))register_buffer("sqrt_alphas_cumprod", torch.sqrt(alphas_cumprod))register_buffer("sqrt_one_minus_alphas_cumprod", torch.sqrt(1.0 - alphas_cumprod))register_buffer("posterior_variance", posterior_variance) timesteps, *_ = betas.shapeself.num_timesteps = int(timesteps) self.sampling_timesteps = timesteps self.normalize = normalize_to_neg_one_to_one if auto_normalize else identityself.unnormalize = unnormalize_to_zero_to_one if auto_normalize else identity @torch.inference_mode()def p_sample(self, x: torch.Tensor, timestamp: int) -> torch.Tensor:b, *_, device = *x.shape, x.devicebatched_timestamps = torch.full((b,), timestamp, device=device, dtype=torch.long) preds = self.model(x, batched_timestamps) betas_t = extract(self.betas, batched_timestamps, x.shape)sqrt_recip_alphas_t = extract(self.sqrt_recip_alphas, batched_timestamps, x.shape)sqrt_one_minus_alphas_cumprod_t = extract(self.sqrt_one_minus_alphas_cumprod, batched_timestamps, x.shape) predicted_mean = sqrt_recip_alphas_t * (x - betas_t * preds / sqrt_one_minus_alphas_cumprod_t) if timestamp == 0:return predicted_meanelse:posterior_variance = extract(self.posterior_variance, batched_timestamps, x.shape)noise = torch.randn_like(x)return predicted_mean + torch.sqrt(posterior_variance) * noise @torch.inference_mode()def p_sample_loop(self, shape: tuple, return_all_timesteps: bool = False) -> torch.Tensor:batch, device = shape[0], "mps" img = torch.randn(shape, device=device)# This cause me a RunTimeError on MPS device due to MPS back out of memory# No ideas how to resolve it at this point # imgs = [img] for t in tqdm(reversed(range(0, self.num_timesteps)), total=self.num_timesteps):img = self.p_sample(img, t)# imgs.append(img) ret = img # if not return_all_timesteps else torch.stack(imgs, dim=1) ret = self.unnormalize(ret)return ret def sample(self, batch_size: int = 16, return_all_timesteps: bool = False) -> torch.Tensor:shape = (batch_size, self.channels, self.image_size, self.image_size)return self.p_sample_loop(shape, return_all_timesteps=return_all_timesteps) def q_sample(self, x_start: torch.Tensor, t: int, noise: torch.Tensor = None) -> torch.Tensor:if noise is None:noise = torch.randn_like(x_start) sqrt_alphas_cumprod_t = extract(self.sqrt_alphas_cumprod, t, x_start.shape)sqrt_one_minus_alphas_cumprod_t = extract(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape) return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise def p_loss(self,x_start: torch.Tensor,t: int,noise: torch.Tensor = None,loss_type: str = "l2",) -> torch.Tensor:if noise is None:noise = torch.randn_like(x_start)x_noised = self.q_sample(x_start, t, noise=noise)predicted_noise = self.model(x_noised, t) if loss_type == "l2":loss = F.mse_loss(noise, predicted_noise)elif loss_type == "l1":loss = F.l1_loss(noise, predicted_noise)else:raise ValueError(f"unknown loss type {loss_type}")return loss def forward(self, x: torch.Tensor) -> torch.Tensor:b, c, h, w, device, img_size = *x.shape, x.device, self.image_sizeassert h == w == img_size, f"image size must be {img_size}" timestamp = torch.randint(0, self.num_timesteps, (1,)).long().to(device)x = self.normalize(x)return self.p_loss(x, timestamp)
扩散过程是训练部分的模型。它打开了一个采样接口,允许我们使用已经训练好的模型生成样本。
训练的要点总结
对于训练部分,我们设置了37,000步的训练,每步16个批次。由于GPU内存分配限制,图像大小被限制为128x128。使用指数移动平均(EMA)模型权重每1000步生成样本以平滑采样,并保存模型版本。
在最初的1000步训练中,模型开始捕捉一些特征,但仍然错过了某些区域。在10000步左右,这个模型开始产生有希望的结果,进步变得更加明显。在3万步的最后,结果的质量显著提高,但仍然存在黑色图像。这只是因为模型没有足够的样本种类,真实图像的数据分布并没有完全映射到高斯分布。

有了最终的模型权重,我们可以生成一些图片。尽管由于128x128的尺寸限制,图像质量受到限制,但该模型的表现还是不错的。

注:本文使用的数据集是森林地形的卫星图片,具体获取方式请参考源代码中的ETL部分。
总结
我们已经完整的介绍了有关扩散模型的必要知识,并且使用Pytorch进行了完整的实现,本文的代码:
https://github.com/Camaltra/this-is-not-real-aerial-imagery/
以上がPyTorchを使用したノイズ除去拡散モデルの実装の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

