前回の記事では、特徴正規化とテンソルについて紹介しましたが、次回は、主に PyTorch の簡単な実践方法を紹介する、PyTorch に関する 2 つの簡潔なチュートリアルを書きます。
1. 四則演算
import torcha = torch.tensor([2, 3, 4])b = torch.tensor([3, 4, 5])print("a + b: ", (a + b).numpy())print("a - b: ", (a - b).numpy())print("a * b: ", (a * b).numpy())print("a / b: ", (a / b).numpy())
加算、減算、乗算、除算については説明する必要はありません。出力は次のとおりです:
a + b:[5 7 9]a - b:[-1 -1 -1]a * b:[ 6 12 20]a / b:[0.6666667 0.750.8]
2. 線形回帰
線形回帰が見つかりました。図に示すように、直線は既知の点にできるだけ近いです。
 図 1
図 1
import torchfrom torch import optimdef build_model1():return torch.nn.Sequential(torch.nn.Linear(1, 1, bias=False))def build_model2():model = torch.nn.Sequential()model.add_module("linear", torch.nn.Linear(1, 1, bias=False))return modeldef train(model, loss, optimizer, x, y):model.train()optimizer.zero_grad()fx = model.forward(x.view(len(x), 1)).squeeze()output = loss.forward(fx, y)output.backward()optimizer.step()return output.item()def main():torch.manual_seed(42)X = torch.linspace(-1, 1, 101, requires_grad=False)Y = 2 * X + torch.randn(X.size()) * 0.33print("X: ", X.numpy(), ", Y: ", Y.numpy())model = build_model1()loss = torch.nn.MSELoss(reductinotallow='mean')optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)batch_size = 10for i in range(100):cost = 0.num_batches = len(X) // batch_sizefor k in range(num_batches):start, end = k * batch_size, (k + 1) * batch_sizecost += train(model, loss, optimizer, X[start:end], Y[start:end])print("Epoch = %d, cost = %s" % (i + 1, cost / num_batches))w = next(model.parameters()).dataprint("w = %.2f" % w.numpy())if __name__ == "__main__":main()
(1) メイン関数から始めて、torch.manual_seed(42) を使用して乱数生成器のシードを設定し、生成される乱数シーケンスが実行されるたびに同じになるようにします。この関数は整数パラメータを受け入れます。シードであり、結果の再現性を確保するためのニューラル ネットワークのトレーニングなど、乱数を必要とするシナリオで使用できます。
(2) torch.linspace(-1, 1, 101, require_grad=False) は、次の目的で使用されます。指定された間隔内で等間隔の値のセットを生成します。この関数は 3 つのパラメータを受け入れます: 開始値、終了値、要素数、指定された数の等間隔の値を含むテンソルを返します;
(3 ) build_model1 の内部実装:
- torch.nn.Sequential(torch.nn.Linear(1, 1,bias=False)) nn.Sequential クラスのコンストラクターを使用し、線形層を渡しますこれをパラメータとして追加し、ニューラル ネットワーク モデルを返します。
- build_model2 には build_model1 と同じ機能があり、add_module() メソッドを使用して、linear という名前のサブモジュールを追加します。
(4) torch.nn.MSELoss (reductinotallow='mean') は損失関数を定義します;
optim.SGD(model.parameters(), lr=0.01, moment=0.9) を使用して、確率的勾配降下法 (SGD) 最適化アルゴリズム
トレーニング セットをバッチ サイズで分割し、100 回ループします
(7) 次は、ニューラル ネットワーク モデルをトレーニングするために使用されるトレーニング関数 train です。具体的には、この関数は次のパラメータを受け入れます:
- model: ニューラル ネットワーク モデル、通常は nn.Module から継承されたクラスのインスタンス;
- loss: 損失関数、使用されるモデルの予測値と真の値を計算する 値の差分;
- optimizer: モデルのパラメーターを更新するために使用されるオプティマイザー;
- x: テンソルである入力データtorch.Tensor タイプのテンソル;
- y: ターゲット データは torch.Tensor タイプのテンソルです;
(8) train は、PyTorch トレーニング プロセスで一般的に使用されるメソッドです。
- モデルをトレーニング モードに設定します。つまり、ドロップアウトやバッチ正規化などのトレーニング中に使用される特別な操作を有効にします。
- 新しいラウンドの勾配計算のオプティマイザー;
- 入力データをモデルに渡し、モデルの予測値を計算し、予測値とターゲット データを損失関数に渡して損失値を計算します。 ## 損失値を逆伝播し、モデル パラメーターの勾配を計算します。;
- オプティマイザを使用してモデル パラメーターを更新し、損失値を最小限に抑えます。;
- 損失値;
...Epoch = 95, cost = 0.10514946877956391Epoch = 96, cost = 0.10514946877956391Epoch = 97, cost = 0.10514946877956391Epoch = 98, cost = 0.10514946877956391Epoch = 99, cost = 0.10514946877956391Epoch = 100, cost = 0.10514946877956391w = 1.983. ロジスティック回帰ロジスティック回帰では、曲線を使用して、一連のトレーニングの軌跡を近似的に表現します。図に示すように:
 図 2
図 2
import numpy as npimport torchfrom torch import optimfrom data_util import load_mnistdef build_model(input_dim, output_dim):return torch.nn.Sequential(torch.nn.Linear(input_dim, output_dim, bias=False))def train(model, loss, optimizer, x_val, y_val):model.train()optimizer.zero_grad()fx = model.forward(x_val)output = loss.forward(fx, y_val)output.backward()optimizer.step()return output.item()def predict(model, x_val):model.eval()output = model.forward(x_val)return output.data.numpy().argmax(axis=1)def main():torch.manual_seed(42)trX, teX, trY, teY = load_mnist(notallow=False)trX = torch.from_numpy(trX).float()teX = torch.from_numpy(teX).float()trY = torch.tensor(trY)n_examples, n_features = trX.size()n_classes = 10model = build_model(n_features, n_classes)loss = torch.nn.CrossEntropyLoss(reductinotallow='mean')optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)batch_size = 100for i in range(100):cost = 0.num_batches = n_examples // batch_sizefor k in range(num_batches):start, end = k * batch_size, (k + 1) * batch_sizecost += train(model, loss, optimizer,trX[start:end], trY[start:end])predY = predict(model, teX)print("Epoch %d, cost = %f, acc = %.2f%%"% (i + 1, cost / num_batches, 100. * np.mean(predY == teY)))if __name__ == "__main__":main() (1) 上で紹介した main 関数から始めます torch.manual_seed( 42)、ここでは省略します ; (2)load_mnist は、mnist データセットをダウンロードする独自の実装であり、trX と teX を入力データとして、trY と teY をラベル データとして返します; ( 3) build_model の内部実装: torch.nn .Sequential(torch.nn.Linear(input_dim, Output_dim,bias=False)) は、線形層を含むニューラル ネットワーク モデルを構築するために使用されます。モデルの入力特徴の数は次のとおりです。 input_dim、出力特徴の数はoutput_dim、線形層にはバイアス項がありません。ここで、n_classes=10は10個のカテゴリを出力することを意味します。
書き換え後:
(3) build_model の内部実装: torch.nn.Sequential(torch.nn.Linear(input_dim, Output_dim,bias=False)) を使用して、線形層を含むニューラル ネットワーク モデルを構築します。モデルの入力特徴の数はinput_dim.出力特徴の数はoutput_dimであり、線形層にはバイアス項がありません。このうち、n_classes=10 は 10 個のカテゴリを出力することを意味します; (4) 他の手順は、損失関数、勾配降下オプティマイザを定義し、batch_size でトレーニング セットを分割し、train に対して 100 回ループすることです。 #optim.SGD(model.parameters(), lr=0.01, moment=0.9) を使用して確率的勾配降下法 (SGD) 最適化アルゴリズムを実装します
(6) 各ラウンドの終了時にトレーニング 最後に、予測を行うには、predict 関数を実行する必要があります。この関数は、model (トレーニング済みモデル) と teX (予測する必要があるデータ) の 2 つのパラメーターを受け入れます。具体的な手順は次のとおりです。
- model.eval()模型设置为评估模式,这意味着模型将不会进行训练,而是仅用于推理;
- 将output转换为NumPy数组,并使用argmax()方法获取每个样本的预测类别;
(7)print("Epoch %d, cost = %f, acc = %.2f%%" % (i + 1, cost / num_batches, 100. * np.mean(predY == teY)))最后打印当前训练的轮次,损失值和acc,上述的代码输出如下(执行很快,但是准确率偏低):
...Epoch 91, cost = 0.252863, acc = 92.52%Epoch 92, cost = 0.252717, acc = 92.51%Epoch 93, cost = 0.252573, acc = 92.50%Epoch 94, cost = 0.252431, acc = 92.50%Epoch 95, cost = 0.252291, acc = 92.52%Epoch 96, cost = 0.252153, acc = 92.52%Epoch 97, cost = 0.252016, acc = 92.51%Epoch 98, cost = 0.251882, acc = 92.51%Epoch 99, cost = 0.251749, acc = 92.51%Epoch 100, cost = 0.251617, acc = 92.51%
4、神经网络
一个经典的LeNet网络,用于对字符进行分类,如图:
 图3
图3
- 定义一个多层的神经网络
- 对数据集的预处理并准备作为网络的输入
- 将数据输入到网络
- 计算网络的损失
- 反向传播,计算梯度
import numpy as npimport torchfrom torch import optimfrom data_util import load_mnistdef build_model(input_dim, output_dim):return torch.nn.Sequential(torch.nn.Linear(input_dim, 512, bias=False),torch.nn.Sigmoid(),torch.nn.Linear(512, output_dim, bias=False))def train(model, loss, optimizer, x_val, y_val):model.train()optimizer.zero_grad()fx = model.forward(x_val)output = loss.forward(fx, y_val)output.backward()optimizer.step()return output.item()def predict(model, x_val):model.eval()output = model.forward(x_val)return output.data.numpy().argmax(axis=1)def main():torch.manual_seed(42)trX, teX, trY, teY = load_mnist(notallow=False)trX = torch.from_numpy(trX).float()teX = torch.from_numpy(teX).float()trY = torch.tensor(trY)n_examples, n_features = trX.size()n_classes = 10model = build_model(n_features, n_classes)loss = torch.nn.CrossEntropyLoss(reductinotallow='mean')optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)batch_size = 100for i in range(100):cost = 0.num_batches = n_examples // batch_sizefor k in range(num_batches):start, end = k * batch_size, (k + 1) * batch_sizecost += train(model, loss, optimizer,trX[start:end], trY[start:end])predY = predict(model, teX)print("Epoch %d, cost = %f, acc = %.2f%%"% (i + 1, cost / num_batches, 100. * np.mean(predY == teY)))if __name__ == "__main__":main()
(1)以上这段神经网络的代码与逻辑回归没有太多的差异,区别的地方是build_model,这里是构建一个包含两个线性层和一个Sigmoid激活函数的神经网络模型,该模型包含一个输入特征数量为input_dim,输出特征数量为output_dim的线性层,一个Sigmoid激活函数,以及一个输入特征数量为512,输出特征数量为output_dim的线性层;
(2)print("Epoch %d, cost = %f, acc = %.2f%%" % (i + 1, cost / num_batches, 100. * np.mean(predY == teY)))最后打印当前训练的轮次,损失值和acc,上述的代码输入如下(执行时间比逻辑回归要长,但是准确率要高很多):
第91个时期,费用= 0.054484,准确率= 97.58%第92个时期,费用= 0.053753,准确率= 97.56%第93个时期,费用= 0.053036,准确率= 97.60%第94个时期,费用= 0.052332,准确率= 97.61%第95个时期,费用= 0.051641,准确率= 97.63%第96个时期,费用= 0.050964,准确率= 97.66%第97个时期,费用= 0.050298,准确率= 97.66%第98个时期,费用= 0.049645,准确率= 97.67%第99个时期,费用= 0.049003,准确率= 97.67%第100个时期,费用= 0.048373,准确率= 97.68%
以上が機械学習 | PyTorch の簡潔なチュートリアル パート 1の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
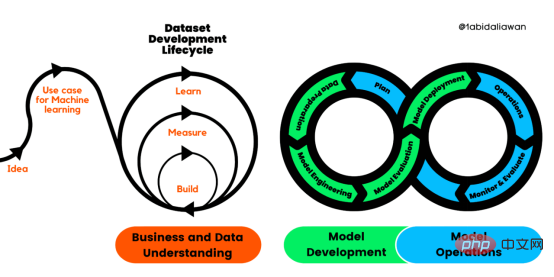 解读CRISP-ML(Q):机器学习生命周期流程Apr 08, 2023 pm 01:21 PM
解读CRISP-ML(Q):机器学习生命周期流程Apr 08, 2023 pm 01:21 PM译者 | 布加迪审校 | 孙淑娟目前,没有用于构建和管理机器学习(ML)应用程序的标准实践。机器学习项目组织得不好,缺乏可重复性,而且从长远来看容易彻底失败。因此,我们需要一套流程来帮助自己在整个机器学习生命周期中保持质量、可持续性、稳健性和成本管理。图1. 机器学习开发生命周期流程使用质量保证方法开发机器学习应用程序的跨行业标准流程(CRISP-ML(Q))是CRISP-DM的升级版,以确保机器学习产品的质量。CRISP-ML(Q)有六个单独的阶段:1. 业务和数据理解2. 数据准备3. 模型
 2023年机器学习的十大概念和技术Apr 04, 2023 pm 12:30 PM
2023年机器学习的十大概念和技术Apr 04, 2023 pm 12:30 PM机器学习是一个不断发展的学科,一直在创造新的想法和技术。本文罗列了2023年机器学习的十大概念和技术。 本文罗列了2023年机器学习的十大概念和技术。2023年机器学习的十大概念和技术是一个教计算机从数据中学习的过程,无需明确的编程。机器学习是一个不断发展的学科,一直在创造新的想法和技术。为了保持领先,数据科学家应该关注其中一些网站,以跟上最新的发展。这将有助于了解机器学习中的技术如何在实践中使用,并为自己的业务或工作领域中的可能应用提供想法。2023年机器学习的十大概念和技术:1. 深度神经网
 基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM
基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM译者 | 朱先忠审校 | 孙淑娟在我之前的博客中,我们已经了解了如何使用因果树来评估政策的异质处理效应。如果你还没有阅读过,我建议你在阅读本文前先读一遍,因为我们在本文中认为你已经了解了此文中的部分与本文相关的内容。为什么是异质处理效应(HTE:heterogenous treatment effects)呢?首先,对异质处理效应的估计允许我们根据它们的预期结果(疾病、公司收入、客户满意度等)选择提供处理(药物、广告、产品等)的用户(患者、用户、客户等)。换句话说,估计HTE有助于我
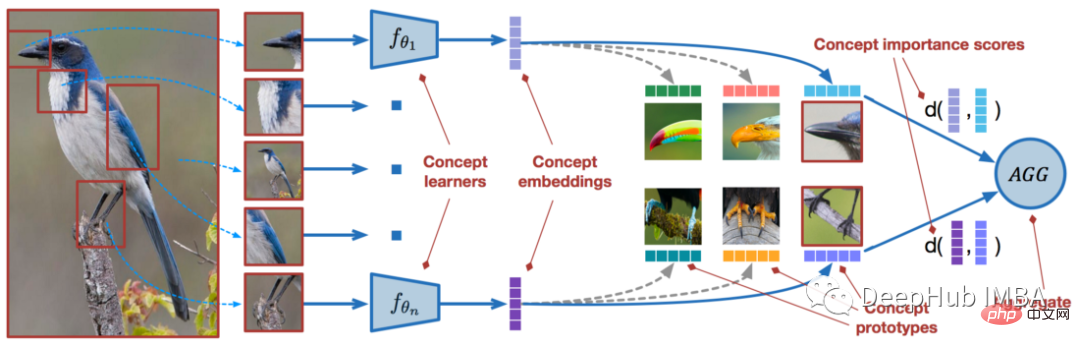 使用PyTorch进行小样本学习的图像分类Apr 09, 2023 am 10:51 AM
使用PyTorch进行小样本学习的图像分类Apr 09, 2023 am 10:51 AM近年来,基于深度学习的模型在目标检测和图像识别等任务中表现出色。像ImageNet这样具有挑战性的图像分类数据集,包含1000种不同的对象分类,现在一些模型已经超过了人类水平上。但是这些模型依赖于监督训练流程,标记训练数据的可用性对它们有重大影响,并且模型能够检测到的类别也仅限于它们接受训练的类。由于在训练过程中没有足够的标记图像用于所有类,这些模型在现实环境中可能不太有用。并且我们希望的模型能够识别它在训练期间没有见到过的类,因为几乎不可能在所有潜在对象的图像上进行训练。我们将从几个样本中学习
 LazyPredict:为你选择最佳ML模型!Apr 06, 2023 pm 08:45 PM
LazyPredict:为你选择最佳ML模型!Apr 06, 2023 pm 08:45 PM本文讨论使用LazyPredict来创建简单的ML模型。LazyPredict创建机器学习模型的特点是不需要大量的代码,同时在不修改参数的情况下进行多模型拟合,从而在众多模型中选出性能最佳的一个。 摘要本文讨论使用LazyPredict来创建简单的ML模型。LazyPredict创建机器学习模型的特点是不需要大量的代码,同时在不修改参数的情况下进行多模型拟合,从而在众多模型中选出性能最佳的一个。本文包括的内容如下:简介LazyPredict模块的安装在分类模型中实施LazyPredict
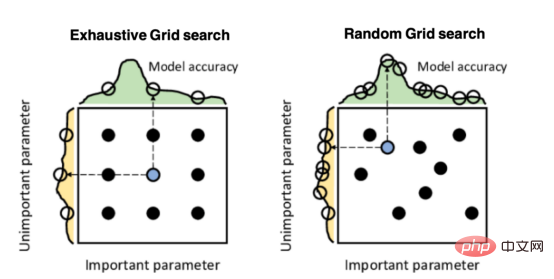 Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM
Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM译者 | 朱先忠审校 | 孙淑娟引言模型超参数(或模型设置)的优化可能是训练机器学习算法中最重要的一步,因为它可以找到最小化模型损失函数的最佳参数。这一步对于构建不易过拟合的泛化模型也是必不可少的。优化模型超参数的最著名技术是穷举网格搜索和随机网格搜索。在第一种方法中,搜索空间被定义为跨越每个模型超参数的域的网格。通过在网格的每个点上训练模型来获得最优超参数。尽管网格搜索非常容易实现,但它在计算上变得昂贵,尤其是当要优化的变量数量很大时。另一方面,随机网格搜索是一种更快的优化方法,可以提供更好的
 人工智能自动获取知识和技能,实现自我完善的过程是什么Aug 24, 2022 am 11:57 AM
人工智能自动获取知识和技能,实现自我完善的过程是什么Aug 24, 2022 am 11:57 AM实现自我完善的过程是“机器学习”。机器学习是人工智能核心,是使计算机具有智能的根本途径;它使计算机能模拟人的学习行为,自动地通过学习来获取知识和技能,不断改善性能,实现自我完善。机器学习主要研究三方面问题:1、学习机理,人类获取知识、技能和抽象概念的天赋能力;2、学习方法,对生物学习机理进行简化的基础上,用计算的方法进行再现;3、学习系统,能够在一定程度上实现机器学习的系统。
 超参数优化比较之网格搜索、随机搜索和贝叶斯优化Apr 04, 2023 pm 12:05 PM
超参数优化比较之网格搜索、随机搜索和贝叶斯优化Apr 04, 2023 pm 12:05 PM本文将详细介绍用来提高机器学习效果的最常见的超参数优化方法。 译者 | 朱先忠审校 | 孙淑娟简介通常,在尝试改进机器学习模型时,人们首先想到的解决方案是添加更多的训练数据。额外的数据通常是有帮助(在某些情况下除外)的,但生成高质量的数据可能非常昂贵。通过使用现有数据获得最佳模型性能,超参数优化可以节省我们的时间和资源。顾名思义,超参数优化是为机器学习模型确定最佳超参数组合以满足优化函数(即,给定研究中的数据集,最大化模型的性能)的过程。换句话说,每个模型都会提供多个有关选项的调整“按钮


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

MinGW - Minimalist GNU for Windows
このプロジェクトは osdn.net/projects/mingw に移行中です。引き続きそこでフォローしていただけます。 MinGW: GNU Compiler Collection (GCC) のネイティブ Windows ポートであり、ネイティブ Windows アプリケーションを構築するための自由に配布可能なインポート ライブラリとヘッダー ファイルであり、C99 機能をサポートする MSVC ランタイムの拡張機能が含まれています。すべての MinGW ソフトウェアは 64 ビット Windows プラットフォームで実行できます。

AtomエディタMac版ダウンロード
最も人気のあるオープンソースエディター

ドリームウィーバー CS6
ビジュアル Web 開発ツール

VSCode Windows 64 ビットのダウンロード
Microsoft によって発売された無料で強力な IDE エディター

ホットトピック
 7433
7433 15
15 1359
1359 52
52



