Tao Zhexuan 氏が Copilot を使い始める: 信じられないほど、定理の名前から私が望む方向を推測できます。

GPT-4 を試した後、Tao Zhexuan は再び Github Copilot を使用しました。

今回の彼の試験シナリオは、リーン言語を学習し、それを使用して数学の定理を形式化することでした。

# 大規模なモデルの場合、形式的な定理の証明も課題です。正式な証明は本質的にはコンピュータ プログラムですが、C や Python による従来のプログラムとは異なり、証明の正しさはリーン言語などの証明アシスタントを使用して検証できます。定理証明はコード生成の特殊な形式であり、評価が非常に厳密であり、モデルに幻想が入る余地がありません。

テレンス タオが言及した定理は、10 月 9 日の論文から来ています:

論文の証明は 1 ページ未満ですが、テレンス タオの公式証明には 200 行の無駄のない言語が使用されます。

たとえば、論文の中で、Tao Zhexuan は、a>0 について、 は実数では凸であると主張しています (これは通常の微積分の演習であるため)。その後、ジェンセンの不等式を呼び出しますが、それには時間がかかりました。すべての詳細を記述するには約 50 行のコードが必要です。

Tao Zhexuan 氏は、さまざまな日常的な検証のために複数行のコードを正確に予測し、定理の名前などの手がかりから目的の方向を推測する Github 副操縦士の能力は「信じられないほど」であると述べました。

Lean の「書き換え」戦略は不可欠であり、式を完全に入力しなくても、式を操作する対象を絞った置換によって、長い仮定や目標を変更できます。

「LaTeX で証明を書くとき、扱いたい長い式を 1 行から次の行に切り取って貼り付け、それに応じて編集するという方法でこの方法を大まかにシミュレートしますが、これによりタイプミスが発生することがあります。文書内の複数の行にまたがっているため、自動的かつ検証可能な方法で書き直せるのは良いことです。」

論文では、不等式、つまり、任意の k、l、n が満たされることについても言及しています。 、次に

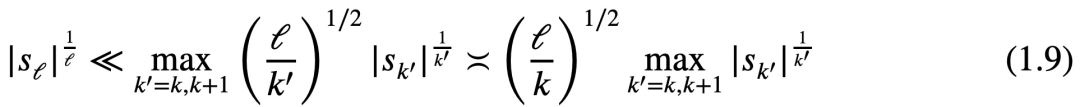Tao Zhexuan は、次の目標はこの不等式の単純なバージョン、つまり不等式 (1.8) を論文で確立することであると述べました。

#このパートの証明では主に微積分の知識が使用されますが、難点の 1 つは漸近記号を使用する必要があることです。陶哲軒氏は、その後のデモンストレーションには時間がかかるものの、特に難しいことではないと述べた。

しかし、現在のツールにはまだいくつかの制限があります。たとえば、バインドされた変数 (シーケンス内の合計変数など) を含む式を書き直すのは必ずしも簡単ではありません。完了。彼は、自然言語 LLM にそのような変換を実行するよう簡単に要求できる日を楽しみにしています...

参考リンク: https:// mathstodon.xyz/@tao/111271244206606941

以上がTao Zhexuan 氏が Copilot を使い始める: 信じられないほど、定理の名前から私が望む方向を推測できます。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。