メビウスの輪を作るのに必要な紙テープの最小の長さはどれくらいですか? 50年来の謎が解けた

メビウスの輪を自分で作ったことがありますか?

メビウスの輪は、独特の数学的構造です。このような美しい片面を構築するのは実は非常に簡単で、子供でも簡単に完成させることができます。紙テープを 1 回ねじって、両端をテープで留めるだけです。しかし、このような簡単に作成できるメビウスの輪には、長い間数学者の興味を惹きつけてきた複雑な特性があります。

最近、研究者たちは、メビウスの輪を作るのに必要な紙テープの最小の長さはどれくらいかという、一見単純な疑問に悩まされています。ブラウン大学のリチャード・エヴァン・シュワルツ氏は、メビウスの輪は「埋め込まれている」のではなく「埋め込まれている」、つまり互いに貫通したり交差したりしていないため、この問題は解決されないと述べた。メビウスの輪は実際にはホログラムであり、3 次元空間に投影された図形です。「埋め込まれた」メビウスの輪の場合、壁を通過する幽霊のように、複数の層のストリップが互いに重なり合うことができます。「埋め込まれた」メビウスの場合ストリップ では、そのような重複はありません。

1977 年、数学者のチャールズ シドニー ウィーバーとベンジャミン リグラー ハルパーンは、最小寸法に関するこの問題を尋ね、メビウスの帯が自己交差することが許可されている場合、これは問題は簡単です。残りの問題は、自己交差を避けるためにどのくらいのスペースが必要かを判断することです。ハルパーンとウィーバーは最小サイズを提案しましたが、その考えを証明できなかったため、これはハルパーン・ウィーバー予想として知られるようになりました。

シュワルツ氏は 4 年前に初めてこの問題について知り、その魅力に魅了されました。今、彼の興味は新たな実へと変わった。

論文アドレス: https://arxiv.org/pdf/2308.12641.pdf

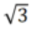彼は参加します2023 ハルパーン・ウィーバー予想は、8 月 24 日に arXiv.org に投稿されたプレプリント論文で証明されました。彼は、紙で作られた「埋め込まれた」メビウスの輪は、アスペクト比が より大きい場合にのみ構築できることを実証しました。たとえば、ストラップの長さが 1 cm の場合、その幅は cm より大きくなければなりません。

このパズルを解くには、数学的な創造性が必要です。この種の問題を解決するための標準的なアプローチを取る場合、自己交差面と非自己交差面を数式で区別することは困難です。この困難を克服するにはシュワルツの幾何学的なビジョンが必要ですが、これはまれです。

シュワルツの証明では、問題を扱いやすい部分に分割することに成功しました。各部分を解くのに基本的に必要なのは、幾何学の基本的な知識のみです。

実際、シュワルツ氏は効果的な戦略を見つけるまで、数年間他の戦略を何度も試しました。彼は最近、2021 年の論文で使用した手法が有効であるはずだと常に感じていたため、この問題を再検討することにしました。

彼の直感は明らかに正しかったです。彼がこの問題を再検討したとき、前の論文の T チャートに関連する補題の誤りに気づきました。この誤りを修正することにより、シュワルツはハルパーン・ウィーバー予想を迅速かつ簡単に証明しました。シュワルツ自身は、あの間違いがなければ3年前に問題を解決していただろうと述べている。

#が重要です。この補題は、メビウスの帯上のいくつかの直線は線織面と呼ばれるという基本的な考え方に基づいています。シュワルツは、空間上の紙片は、たとえそれが複雑な位置にあったとしても、各点で紙片を通る直線を持っていると指摘し、これらの直線をメビウスの帯を横切り、両端が接触するように描くことを想像することができます。国境。

前回の研究で、シュワルツは、同じ平面内にある互いに平行な 2 つの直線が各 T パターンでメビウスの帯を形成していることを確認しました。彼は、これらのものが存在することは明らかではなく、証明する必要があること、これが補題を証明する最初の部分であると指摘しています。

次のステップは、最適化問題を設定して解くことです。これには、メビウスの帯を、ストリップの幅を延長する線分に沿って斜めに切断し、次の結果を得る必要があります。最終的な形。シュワルツ氏は2021年の論文で、その形状は平行四辺形であると誤って結論付けた。

この夏、シュワルツは別のやり方を試してみることにしました。彼はメビウスの輪を平らにしようと試み始めました。それらを平面に押し込むことができることが示されれば、この複雑な問題は、より扱いやすい平面の問題に帰着するでしょう。シュワルツは実験でメビウスの輪を切り開いたところ、それが平行四辺形ではなく台形であることに気づきました。

ついに、50年来の疑問が解決されました。長年の問題を解決しようとするのは勇気が必要ですが、これがシュワルツの数学における強みです。彼は比較的簡単そうに見えて実際は難しい問題に取り組むのが好きです。彼は、これまでの研究者が気づかなかった問題に気づくでしょう。

^{参考リンク: https://www.scientificamerican.com/article/mathematicians-solve-50-year-旧メビウスの帯パズル1/}

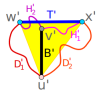
以上がメビウスの輪を作るのに必要な紙テープの最小の長さはどれくらいですか? 50年来の謎が解けたの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。