
書き直された内容は次のとおりです: Ziluo
複雑な電子相互作用の大規模シミュレーションは、依然として原子モデリングにおける最大の課題の 1 つです。古典的な力場は電子状態とイオンの再配列の間の結合を説明できないことがよくありますが、より正確な非経験的分子動力学は計算の複雑さに悩まされ、研究手法に関連する長時間かつ大規模なシミュレーションを妨げます。この現象は非常に重要です
##最近、カリフォルニア大学バークレー校とローレンス バークレー国立研究所の研究者は、グラフ ニューラル ネットワークに基づく機械学習原子間ポテンシャル (MLIP) モデルを提案しました。結晶ハミルトニアン グラフ ニューラル ネットワーク (Crystal Hamiltonian Graph Neural Network、CHGNet) は、モデル化できます。普遍的な位置エネルギー面。 この研究は、適切な化学反応を捕捉するための電荷情報の重要性を強調し、以前の MLIP では観察できなかった追加の電子的自由度を備えたイオンシステムに関する洞察を提供します。 この研究は「電荷情報に基づいた原子論的モデリングのための事前学習済みユニバーサル ニューラル ネットワークの可能性としての CHGNet」というタイトルで、2023 年 9 月 14 日に「Nature Machine Intelligence」に掲載されました。
CHGNet は、材料プロジェクト軌跡データセット (MPtrj) からのエネルギー、力、応力、磁気モーメントに関して事前トレーニングされています。このデータセットには、150 万個の無機構造に関する 10 年以上の密度汎関数理論の計算が含まれています。磁気モーメントを明示的に含めることにより、CHGNet は電子の軌道占有を学習して正確に表現できるため、原子および電子の自由度を記述する能力が強化されます。
MPtrj 元素の分布データ セット内の要素を以下に示します。 表示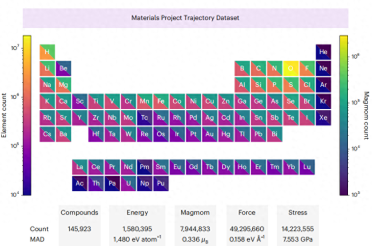
 #書き換えられた内容は次のとおりです。 図: CHGNet モデル アーキテクチャ。 (出典: 論文)
#書き換えられた内容は次のとおりです。 図: CHGNet モデル アーキテクチャ。 (出典: 論文)
CHGNet では、元の単位の各原子 vi の  内に隣接する原子 vj を検索することにより、周期的な結晶構造が原子グラフ
内に隣接する原子 vj を検索することにより、周期的な結晶構造が原子グラフ  に変換されます。
に変換されます。
の後に更新されたアトミック特徴がエネルギーの予測に直接使用される他の GNN とは異なり、CHGNet は t−1 畳み込み層のノード特徴を正規化します
は、局所的なイオン環境と電荷分布に関する豊富な情報を保持します。したがって、エネルギー、力、応力を予測するために使用される原子の特徴は、その電荷状態に関する情報によって制約された電荷です。したがって、CHGNet は核の位置と原子のアイデンティティのみを入力として使用して荷電状態情報を提供し、原子モデリングにおける電荷分布の研究を可能にします。 
 固体材料における CHGNet の応用
固体材料における CHGNet の応用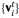
図は、Na2V2(PO4)3 の磁気モーメントと隠れ空間の正規化を示しています。 (論文より引用) 

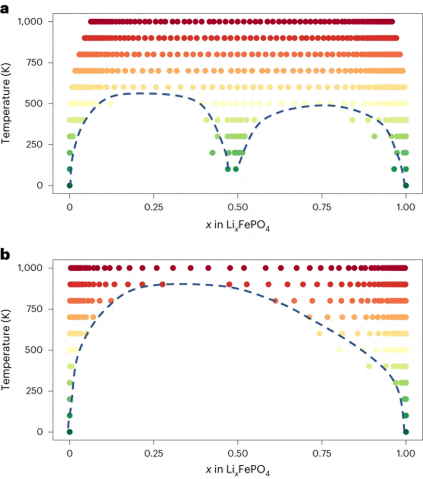 LiMnO2 の研究では、CHGNet が長期の電荷情報 MD を通じて、異価遷移金属酸化物系における電荷の不均化と相転移の間の関係についての洞察を提供できることが実証されました。
LiMnO2 の研究では、CHGNet が長期の電荷情報 MD を通じて、異価遷移金属酸化物系における電荷の不均化と相転移の間の関係についての洞察を提供できることが実証されました。
#リライト内容: 図: Li0.5MnO2 の相転移と電荷微分。 (引用:論文)
次に、一般的な分子動力学シミュレーションにおけるCHGNetの精度を検討しました。私たちはガーネット導体におけるリチウムの拡散を研究対象としています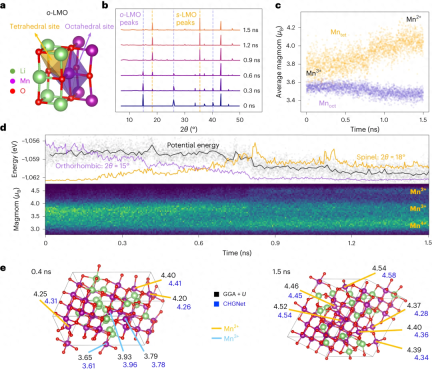
#図: ガーネット Li3La3Te2O12 におけるリチウムの拡散率。 (出典: 論文)
結果は、CHGNet が活性化拡散ネットワーク効果を正確に捕捉できるだけでなく、その活性化エネルギーが DFT 結果と非常に一致していることを示しています。これは、CHGNet が局所環境におけるリチウムイオンの強い相互作用を正確に捕捉でき、高度に非線形な拡散挙動をシミュレートする機能を備えていることを証明しています。さらに、CHGNet はシミュレーションされた拡散速度の誤差を大幅に減らすことができ、ナノ秒シミュレーションに拡張することで、拡散速度の悪いシステムを研究することができます。
第二に、magmom はイオン系のスピン偏極から計算される原子電荷の優れたヒューリスティックですが、非磁性イオンの原子電荷推論があいまいな場合があることが認識されているため、追加の領域知識が必要です。したがって、マグモムのないイオンの場合、原子中心のマグモムは原子の電荷を正確に反映できません。CHGNet は、他の MLIP 関数と同様に、環境から電荷を推測します。
は、他の電荷表現方法を組み合わせることでさらに改善できます。電子位置決め機能、電気分極、原子軌道ベースの分割などの強化されたモデル。これらの手法は、潜在空間における原子特徴量エンジニアリングに使用できます。
CHGNet は、電荷ベースの原子シミュレーションを実装でき、異価系を研究するための大規模な計算シミュレーションに適しているため、計算化学、物理学、材料科学における電荷移動結合現象に関する生物学および研究の機会
論文を表示するには、次のリンクをクリックしてください: https://www.nature.com/articles/s42256-023-00716-3
以上が事前トレーニング済みの汎用ニューラル ネットワーク CHGNet を使用した電荷ベースの原子シミュレーションの実装の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 補強能力のガイド - 分析VidhyaApr 28, 2025 am 09:30 AM
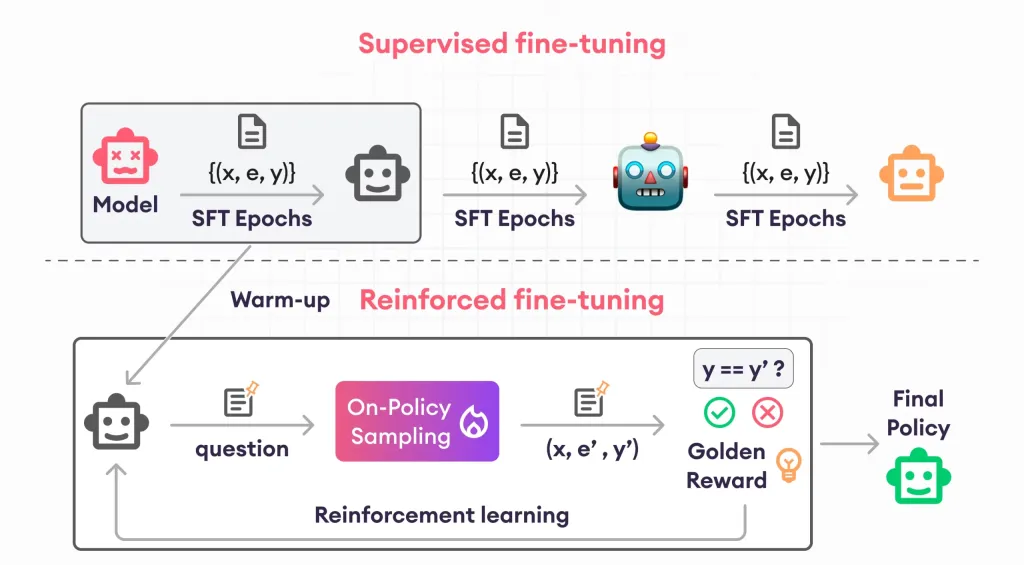
補強能力のガイド - 分析VidhyaApr 28, 2025 am 09:30 AM補強能力は、人間のフィードバックに基づいて調整するためにモデルを教えることにより、AI開発を揺さぶりました。それは、監督された学習基盤と報酬ベースの更新をブレンドして、より安全で、より正確に、そして本当に助けます
 踊りましょう:私たちの人間のニューラルネットを微調整するための構造化された動きApr 27, 2025 am 11:09 AM
踊りましょう:私たちの人間のニューラルネットを微調整するための構造化された動きApr 27, 2025 am 11:09 AM科学者は、彼らの機能を理解するために、人間とより単純なニューラルネットワーク(C. elegansのものと同様)を広く研究してきました。 ただし、重要な疑問が生じます。新しいAIと一緒に効果的に作業するために独自のニューラルネットワークをどのように適応させるのか
 新しいGoogleリークは、Gemini AIのサブスクリプションの変更を明らかにしますApr 27, 2025 am 11:08 AM
新しいGoogleリークは、Gemini AIのサブスクリプションの変更を明らかにしますApr 27, 2025 am 11:08 AMGoogleのGemini Advanced:Horizonの新しいサブスクリプションティア 現在、Gemini Advancedにアクセスするには、1か月あたり19.99ドルのGoogle One AIプレミアムプランが必要です。 ただし、Android Authorityのレポートは、今後の変更を示唆しています。 最新のGoogle p
 データ分析の加速がAIの隠されたボトルネックをどのように解決しているかApr 27, 2025 am 11:07 AM
データ分析の加速がAIの隠されたボトルネックをどのように解決しているかApr 27, 2025 am 11:07 AM高度なAI機能を取り巻く誇大宣伝にもかかわらず、エンタープライズAIの展開内に大きな課題が潜んでいます:データ処理ボトルネック。 CEOがAIの進歩を祝う間、エンジニアはクエリの遅い時間、過負荷のパイプライン、
 MarkitDown MCPは、任意のドキュメントをマークダウンに変換できます!Apr 27, 2025 am 09:47 AM
MarkitDown MCPは、任意のドキュメントをマークダウンに変換できます!Apr 27, 2025 am 09:47 AMドキュメントの取り扱いは、AIプロジェクトでファイルを開くだけでなく、カオスを明確に変えることです。 PDF、PowerPoint、Wordなどのドキュメントは、あらゆる形状とサイズでワークフローをフラッシュします。構造化された取得
 建物のエージェントにGoogle ADKを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:42 AM
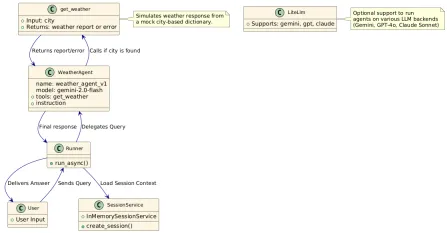
建物のエージェントにGoogle ADKを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:42 AMGoogleのエージェント開発キット(ADK)のパワーを活用して、実際の機能を備えたインテリジェントエージェントを作成します。このチュートリアルは、ADKを使用して会話エージェントを構築し、GeminiやGPTなどのさまざまな言語モデルをサポートすることをガイドします。 w
 効果的な問題解決のためにLLMを介したSLMの使用 - 分析VidhyaApr 27, 2025 am 09:27 AM
効果的な問題解決のためにLLMを介したSLMの使用 - 分析VidhyaApr 27, 2025 am 09:27 AMまとめ: Small Language Model(SLM)は、効率のために設計されています。それらは、リソース不足、リアルタイム、プライバシーに敏感な環境の大手言語モデル(LLM)よりも優れています。 特にドメインの特異性、制御可能性、解釈可能性が一般的な知識や創造性よりも重要である場合、フォーカスベースのタスクに最適です。 SLMはLLMSの代替品ではありませんが、精度、速度、費用対効果が重要な場合に理想的です。 テクノロジーは、より少ないリソースでより多くを達成するのに役立ちます。それは常にドライバーではなく、プロモーターでした。蒸気エンジンの時代からインターネットバブル時代まで、テクノロジーの力は、問題の解決に役立つ範囲にあります。人工知能(AI)および最近では生成AIも例外ではありません
 コンピュータービジョンタスクにGoogle Geminiモデルを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:26 AM
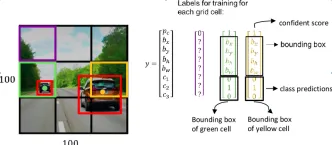
コンピュータービジョンタスクにGoogle Geminiモデルを使用する方法は? - 分析VidhyaApr 27, 2025 am 09:26 AMコンピュータービジョンのためのGoogleGeminiの力を活用:包括的なガイド 大手AIチャットボットであるGoogle Geminiは、その機能を会話を超えて拡張して、強力なコンピュータービジョン機能を網羅しています。 このガイドの利用方法については、


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

mPDF
mPDF は、UTF-8 でエンコードされた HTML から PDF ファイルを生成できる PHP ライブラリです。オリジナルの作者である Ian Back は、Web サイトから「オンザフライ」で PDF ファイルを出力し、さまざまな言語を処理するために mPDF を作成しました。 HTML2FPDF などのオリジナルのスクリプトよりも遅く、Unicode フォントを使用すると生成されるファイルが大きくなりますが、CSS スタイルなどをサポートし、多くの機能強化が施されています。 RTL (アラビア語とヘブライ語) や CJK (中国語、日本語、韓国語) を含むほぼすべての言語をサポートします。ネストされたブロックレベル要素 (P、DIV など) をサポートします。

WebStorm Mac版
便利なJavaScript開発ツール

SAP NetWeaver Server Adapter for Eclipse
Eclipse を SAP NetWeaver アプリケーション サーバーと統合します。

メモ帳++7.3.1
使いやすく無料のコードエディター

VSCode Windows 64 ビットのダウンロード
Microsoft によって発売された無料で強力な IDE エディター

ホットトピック
 7779
7779 15
15 1644
1644 14
14 1399
1399 52
52 1296
1296 25
25 1234
1234 29
29


