グラフの支配的なセットが NP 完全であることを証明する

グラフの支配的なセットは NP 完全問題であり、サブセット内のすべての頂点または隣接する頂点がサブセット内にあるような頂点のサブセットです。 NP の完全な形式は「非決定性多項式」で、問題を多項式時間でチェックします。つまり、解が正しいかどうかを多項式時間でチェックできます。多項式時間は、線形検索時間計算量 – n、 二分探索 – logn、 マージ ソート – n(log)n などのコードに対して最高のパフォーマンスを発揮します。 。 NP 完全グラフは、妥当な時間内に優れた解を提供します。このアプリケーションは、ネットワーク制御、コンピュータ実験室でのトポロジ作成、ソーシャル ネットワーク、分散コンピューティングなどの分野で使用されます。

ノードが NP 完全グラフの支配的なセットを持っているかどうかを理解し、確認してみましょう。

頂点は、それ自体とその隣接する頂点のそれぞれを支配すると言われます。

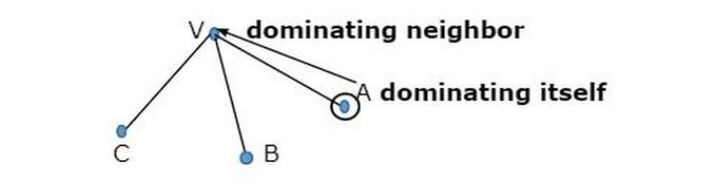
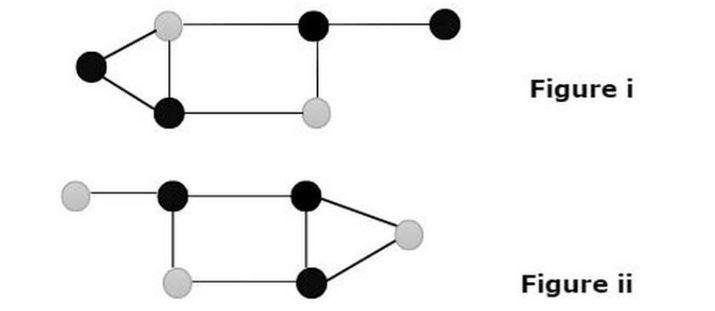
2 つのグラフを見ると、グラフ内のノードの灰色が本質的に優勢であることがわかります。

リーリー

パラメータ

G はグラフとみなされ、V は頂点とみなされ、E はエッジとみなされます。

グラフ G(V, E) と整数 k が与えられた場合、グラフにサイズ k の支配的なセットがあるかどうかを判断します。問題として指定された入力は、問題のインスタンスとみなされます。グラフ G(V, E) と整数 k は、グラフ G が G 内に支配集合を持つことができるかどうかを問う支配集合問題の例として機能します。 NP 完全問題の定義は NP と NP 困難の両方である問題であるため、問題が NP 完全であることの証明には 2 つの要素があります -

NP完全問題におけるドミネーターセット

多項式時間で X に還元できる NP 問題 Y がある場合、X は NP 完全問題です。 NP 完全問題は、NP 問題と同じくらい難しいです。問題が NP 問題と NP 困難問題の両方の一部である場合、その問題は NP 完全です。非決定性チューリング マシンは、多項式時間で NP 完全問題を解くことができます。問題が np-complete である場合、問題には np と np-hard の両方の組み合わせがあります。

これは、np 解の問題が多項式時間で検証できることを意味します。

NP 完全な実際の例には、 -

などの支配的なセットがあります。

• 意思決定の問題。

• グラフィックは一貫しています。

非決定的検索アルゴリズム

リーリー

したがって、このアルゴリズムの合計時間計算量は O(1) ですが、この問題を解決するためにどの検索手法がより有用であるかはわかりません。これは非決定的アルゴリズムと呼ばれます。

NP 困難問題におけるドミネーター セット

多項式時間で問題 X に還元できる NP 完全問題 Y がある場合、問題 X は NP 困難です。 NP 困難問題は、NP 完全問題と同じくらい難しいです。 NP 困難問題は、必ずしも NP カテゴリに属する​​わけではありません。

すべての NP 問題が多項式時間で解ける場合、それは NP 困難と呼ばれます。多くの場合、特定の問題は、他の問題を解決したり軽減したりするために使用されます。

NP ハードの実際の例には、-

のような支配的なセットがあります。

• ハミルトニアン回路

＃＃＃＃＃＃最適化＃＃＃＃＃＃

• 最短ルート

• ＃＃＃結論は＃＃＃

  私たちは、グラフの支配的な集合が NP 完全であるという概念を学びました。ハミルトンサイクルや最短経路など、離散数学がこれらの問題を結び付ける重要な側面であることがわかります。プログラミング用語では、NP 完全問題は、見つけるのは困難ですが、その解は多項式時間で直接検証できる問題のクラスです。

以上がグラフの支配的なセットが NP 完全であることを証明するの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。