配列内の逆対数を計算するためにマージ ソート アルゴリズムを使用して記述された C/C++ プログラムですか?

指定された配列をソートするときに発生する逆転カウントは、逆転カウントと呼ばれます。逆問題は、マージ ソート アルゴリズムを使用して解決できる古典的な問題です。この問題では、v より大きい左側の要素をすべてカウントし、そのカウントを出力に追加します。このロジックは、マージ ソートのマージ機能で完成します。

このトピックをよりよく理解するために、例を挙げてみましょう。マージ プロセスに関係する 2 つのサブ配列を考えてみましょう -

##

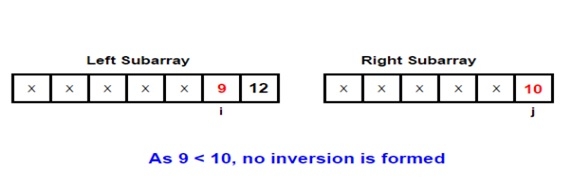
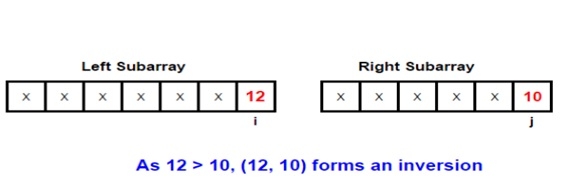
Input: arr[] = { 1, 9, 6, 4, 5}
Output: Inversion count is 5

説明

配列の反転回数

配列を与えて、反転回数を求めます。 (i A[j]) の場合、ペア (i, j) は配列 A の反転と呼ばれます。 arr 内のそのようなペアをすべてカウントする必要があります

たとえば、配列には 5 つの反転があります

(9,6), (9,4), ( 9,5)、(6,4)、(6,5)

1. 要素の値を相互に比較します。

2. 下のインデックスの値が大きい場合は、カウンターをインクリメントします。

3. 結果を表示します。

例

#include <stdio.h>
int Merge(int arr[], int aux[], int low, int mid, int high) {
   int k = low, i = low, j = mid + 1;
   int inversionCount = 0;
   while (i <= mid && j <= high) {
      if (arr[i] <= arr[j]) {
         aux[k++] = arr[i++];
      } else {
         aux[k++] = arr[j++];
         inversionCount += (mid - i + 1); // NOTE
      }
   }
   while (i <= mid)
   aux[k++] = arr[i++];
   for (int i = low; i <= high; i++)
      arr[i] = aux[i];
   return inversionCount;
}
int MergeSort(int arr[], int aux[], int low, int high) {
   if (high == low) // if run size == 1
      return 0;
   int mid = (low + ((high - low) >> 1));
   int inversionCount = 0;
   inversionCount += MergeSort(arr, aux, low, mid);
   inversionCount += MergeSort(arr, aux, mid + 1, high);
   inversionCount += Merge(arr, aux, low, mid, high);
   return inversionCount;
}
int main() {
   int arr[] = { 1, 9, 6, 4, 5 };
   int N = 5;
   int aux[N];
   for (int i = 0; i < N; i++)
      aux[i] = arr[i];
   printf("Inversion count is %d", MergeSort(arr, aux, 0, N - 1));
   return 0;
}

以上が配列内の逆対数を計算するためにマージ ソート アルゴリズムを使用して記述された C/C++ プログラムですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。