平面内の同一線上にある点が 2 つ以下の場合、三角形の数はいくつですか?

n 点が与えられた平面上の三角形の数を数え、同一線上にある点の数を 2 つ以下に制限する方法を見てみましょう。

共線点が 2 つ以下である平面内の三角形の数を計算することは、コンピュータ グラフィックス、画像処理、およびその他のコンピュータ サイエンスの分野に適用される計算幾何学の典型的な問題です。

たとえば、3D グラフィックスの 3D シーンから 2D イメージを作成する場合、共線点が 2 つ以下の平面内で三角形を計算するという問題が発生することがあります。この場合、三角形カウント プロセスを使用して、3D シーンを平面に投影した後の最終 2D 画像にいくつの三角形が存在するかを判断できます。これにより、シーンの複雑さを判断し、レンダリング速度を向上させることができます。

画像処理では、画像内の固有のオブジェクトや形状の数を数えたい場合があります。この問題は役に立ちます。この場合、画像を平面上の点の集合として表すことができ、三角形カウント手法を適用することで、これらの点の間に作成できる三角形の数を数えることができます。形成された三角形の数を数えることによって、画像内のさまざまなアイテムや形状のおおよその数を判断できます。

イラスト

いくつかの例を通してこの問題を理解し、解決してみましょう。

目的は、同一直線上にある点が 2 つ以下となるように、n 個の点を持つ平面上に形成される三角形の数を決定することです。

＃＃＃＃＃＃例 - ＃＃＃＃＃＃

N が平面上の点の数であると仮定します。 N = 3

これらの点を使用すると、三角形を描くことしかできません。

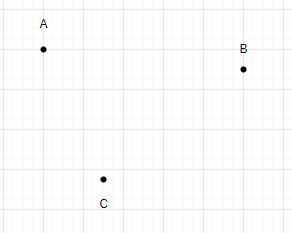したがって、3 つの点を使用して形成される三角形の総数は 1 です。

N = 4 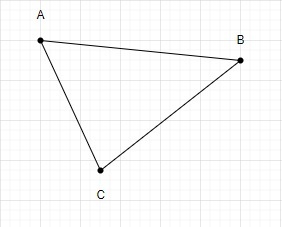とします

この 4 つの点を使って三角形を描いてみましょう。

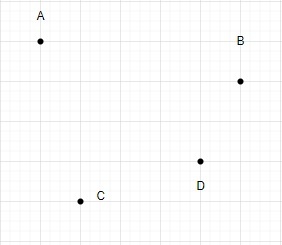4 つの点を使用して形成される三角形の総数は 4 です。

三角形の数の計算に必要な数学をいくつか見てみましょう。これは、順列と組み合わせを使用して取得できます。三角形を構築するには、一度に合計から 3 点が必要です。

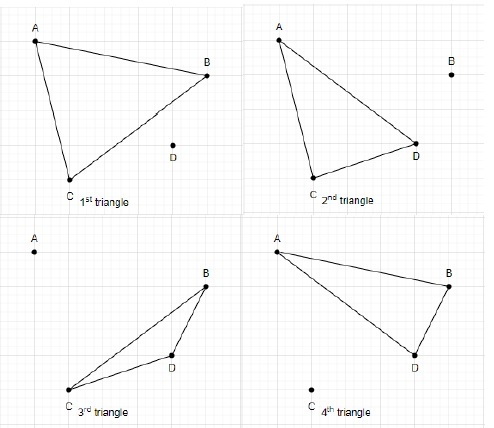
したがって、平面に n 個の点が含まれており、そのうちの 2 つだけが同一線上にある場合、平面内の三角形の数は次の式で求められます。

$$\mathrm{n_{C_{3}}\:=\:\frac{n(n-1)\:(n-2)}{6}}$$

＃＃＃方法＃＃＃

プログラムは、次のアルゴリズムを使用して、同一線上にある点が 2 つ以下の場合に、平面内の三角形の数を見つけます。

平面上の点の数を入力として取得し、同一線上にある点を 2 つ以下に制限します。

上記の式を使用して、三角形の合計数を計算します。
三角形の合計数を出力として出力します。

• ＃＃＃例＃＃＃
C 同一線上にある点が 2 つ以下の場合に、平面内の三角形の数を計算するプログラム。
• リーリー ＃＃＃出力＃＃＃ リーリー ＃＃＃複雑＃＃＃
  時間計算量
: O(1)。このコードは、入力サイズに関係なく、固定数の計算を実行するためです。

空間複雑度

: O(1)。コードは、入力のサイズに関係なく、入力値と結果を保存するために固定数の変数を使用するためです。

＃＃＃結論は＃＃＃

この記事では、同一直線上にある 2 つの点がないという制約のもとで、n 個の点が与えられた可能な三角形の総数を見つける方法を説明しようとします。この記事がこの概念をより深く学ぶのに役立つことを願っています。

以上が平面内の同一線上にある点が 2 つ以下の場合、三角形の数はいくつですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。