中点を繰り返し結んでできる正方形の面積は何ですか?
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB転載
- 2023-09-03 22:21:101489ブラウズ
正方形の面積は、正方形の辺の長さの積に等しい。
各正方形の辺の中点が別の正方形を形成する図形を考えます。特定の数の正方形になるまで同様に続きます。
この図は、正方形の中点を接続して形成される正方形を示しています。
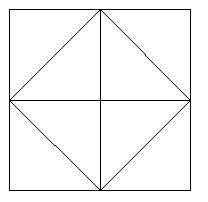
この図の辺の長さを a とすると、
内部正方形の辺の長さは
L2 = (a/2)<sup>2</sup> + (a/2)<sup>2</sup>
L2 = a<sup>2</sup>(1/4 + 1/4) = a<sup>2</sup>(1/2) = a<sup>2</sup>/2
L = a<sup>2</sup>/ (\sqrt{2}).面積となります。正方形 2 = L2 = a2/2.
次の正方形の場合、正方形 3 の面積 = a2/4
例を挙げてみましょう。
ここから、連続する正方形の面積を推定できます。
a2, a2/ 2, a2/ 4, a2/8, …..
これは、公比 1/2 の等比数列です。ここで、a2は最初の項です。
例
#include <stdio.h>
#include <math.h>
int main() {
double L = 2, n = 10;
double firstTerm = L * L;
double ratio = 1 / 2.0;
double are = firstTerm * (pow(ratio, 10)) ;
printf("The area of %lfth square is %lf", n , sum);
return 0;
}出力
The area of 10th square is 0.003906
以上が中点を繰り返し結んでできる正方形の面積は何ですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
声明:
この記事はtutorialspoint.comで複製されています。侵害がある場合は、admin@php.cn までご連絡ください。

