最大 M 個の連続ノードと値 K を持つルートからリーフまでのパスの数
- WBOY転載
- 2023-08-25 22:45:131026ブラウズ
######導入###
バイナリ ツリーは、コンピュータ サイエンスやプログラミングで幅広い用途に使用できる魅力的なデータ構造です。興味深い問題は、親ノードとその子で構成される特定のツリーからカウントを見つけることです。バイナリ ツリーはノードで構成され、ルート ノードが決定され、ルート ノードはユーザーのニーズに応じて子ノードを提供できます。 K値が決まり、M値により移動方法が選択されます。
ルートからリーフへのパスの数
グラフは、整数の形式で値を保持するさまざまなノードを使用して作成されます。この記事では主に、開始ノードまたはルート ノードからリーフ ノードまたは子ノードまでのカウントに焦点を当てます。
###例###
グラフは、さまざまなノードを含むバイナリ ツリーから作成されます。
上記のバイナリ ツリーでは、ルート ノードは「8」として選択されています。
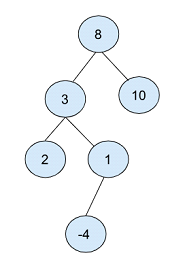
- 次に、ルート ノードの左右の位置を占める 2 つのノードを作成します。1 つは値 3、もう 1 つは値 10 です。
- 値 2 のノードをルートとして、値 2 と 1 をそれぞれ左ノードと右ノードとして別の子ノードを作成します。
- 最後に、値 1 の子ノードは、値 -4 の子ノードを作成します。
- 方法 1: 再帰関数を使用して、K 値を持つ最大 M 個の連続したノードから構成されるルートからリーフへのパスを計算する C コード
この問題を効率的に解決するために、ツリー トラバーサル アルゴリズムや再帰などの基本概念を利用します。
###アルゴリズム###
ステップ 1
: ツリー ノードを表す構造体を作成します。これには、2 つのポインター (左の子ノードと右の子ノード) とノード値を格納する整数フィールドが含まれます。
ステップ 2
: 現在のパスの長さ (0 に初期化)、連続出現数 (0 に初期設定) を追跡しながら、ルートから開始してバイナリ ツリーをトラバースする再帰関数を設計します。およびターゲット値 K を考慮して、連続発生の最大数 M を許可します。ステップ 3
: 左右の各サブツリーで関数を再帰的に呼び出し、増分パスの長さや連続出現数 (該当する場合) などの更新されたパラメーターを渡します。ステップ 4
: トラバーサル中に訪問した空ではないノードごとに:a) その値が K に等しい場合、両方の変数に 1 を加算します。
b) 変数の値が K と一致しない場合、またはパス内でこれまでに検出された M の連続出現数を超える場合は、変数をゼロにリセットします。ステップ 5
: ツリーをトラバースしているときに、子ノードの値が左と右の両方のケースでゼロである場合、これを 2 つの方法で処理できます。a) 変数が M を超えていないかどうかを確認します。
b) 「はい」の場合、条件を満たすパスの総数を 1 つ増やします。
###例### リーリー ###出力### リーリー ###結論は### この記事では、上部 (つまり、葉) から先端または根までのパスの数を数える問題を検討します。このような問題は、C のツリー トラバーサル アルゴリズムと再帰的手法を使用することで効率的に解決できます。バイナリ ツリーをたどるプロセスは難しそうに見えますが、例を使用すると簡単になります。
以上が最大 M 個の連続ノードと値 K を持つルートからリーフまでのパスの数の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
声明:
この記事はtutorialspoint.comで複製されています。侵害がある場合は、admin@php.cn までご連絡ください。

