ホームページ >Java >&#&チュートリアル >毎日使ってください! HASHって知っていますか?
毎日使ってください! HASHって知っていますか?
- Java学习指南転載
- 2023-07-26 14:47:45785ブラウズ
HashMap を使用したことがありますか? それでは、ハッシュとは何かを真剣に理解しましたか? この記事では、ハッシュ アルゴリズムを原理レベルから詳しく学習します。
1. ハッシュの概念
ハッシュ手法の主な考え方は、キー コードに基づいてノードのストレージ アドレスを決定することです。値: キーコードに基づく値 K は独立変数です. 特定の関数関係 h(K) (ハッシュ関数と呼ばれます) を通じて、対応する関数値が計算されます. この値はノードの格納アドレスとして解釈されます,ノードはユニット内のこのストレージに保存されます。取得するときは、同じ方法でアドレスを計算し、対応するユニットに移動して探しているノードを取得します。ノードはハッシュ化によって迅速に取得できます。ハッシュ (「ハッシュ」とも呼ばれる) は、重要な保存方法であり、一般的な取得方法です。
ハッシュ記憶方式に従って構築された記憶構造をハッシュテーブル(ハッシュテーブル)といいます。ハッシュ テーブル内の位置はスロットと呼ばれます。ハッシュ技術の中核はハッシュ関数です。任意の動的ルックアップ テーブル DL に対して、「理想的な」ハッシュ関数 h と対応するハッシュ テーブル HT が選択される場合、DL 内の各データ要素 X に対して。関数値h(X.key)は、ハッシュテーブルHTにおけるXの格納位置である。データ要素 X は、挿入時 (またはテーブルの作成時) にこの位置に配置され、X を取得するときにもこの位置で検索されます。ハッシュ関数によって決定される格納場所は、ハッシュ アドレスと呼ばれます。したがって、ハッシュ関数の核心は、キーコード値 (X.key) とハッシュアドレス h (X.key) の対応関係をハッシュ関数で求め、この関係によって組織的な保存と検索を実現することです。
一般に、ハッシュ テーブルの記憶空間は 1 次元配列 HT[M] であり、ハッシュ アドレスは配列の添字です。ハッシュ手法を設計する目的は、キー値 K に対して特定のハッシュ関数 h、0
2. ハッシュ関数
以下の説明では、整数値のキー コードを扱っていると仮定しますが、それ以外の場合は、いつでも通常の値のキー コードを作成できます。整数間の 1 対 1 の対応により、キーの検索が対応する正の整数の検索に変換され、同時にハッシュ関数の値が 0 と M-1 の間に収まるとさらに仮定されます。ハッシュ関数を選択するための原則は、操作が可能な限り単純であること、関数の値の範囲がハッシュ テーブルの範囲内であること、ノードが可能な限り均等に分散されること、つまり、キーが異なれば、ハッシュ関数の値も異なります。キーの長さ、ハッシュ テーブルのサイズ、キーの分散、レコードの取得頻度など、さまざまな要素を考慮する必要があります。以下に、一般的に使用されるハッシュ関数をいくつか紹介します。
1. 剰余除算法
#剰余除算法は、その名のとおり、キーコード x を M で除算する方法です (多くの場合、ハッシュ テーブルの長さを取得し、残りをハッシュ アドレスとして取得します。剰余法はほぼ最も単純なハッシュ法であり、ハッシュ関数は h(x) = x mod M です。
#2. 乗算剰余方式
#この方式を使用する場合、まずキーコードに定数 A を乗算します (0)。 1) 積の小数部分を抽出します。次に、この値に整数 n を乗算し、その結果を切り捨てて、ハッシュ アドレスとして使用します。ハッシュ関数は次のとおりです: hash (key) = _LOW(n × (A × key % 1))。このうち、「A × key % 1」は A × key の小数部分を取ること、つまり A × key % 1 = A × key - _LOW(A × key) を意味し、_LOW(X) は整数部分を取ることを意味します
整数の除算は通常、乗算よりも実行が遅いため、意識的に剰余の使用を避けてください 法的な演算により実行が改善される可能性がありますハッシュアルゴリズムの時間。 Square-Middle メソッドの具体的な実装は、まずキー コードの 2 乗値を見つけて類似の数値の差を拡大し、次にテーブルの長さに応じて中間の数桁 (多くの場合 2 進ビット) をハッシュとして取得します。関数値。積の中央の桁は乗数の各桁に関連付けられているため、結果として得られるハッシュ アドレスはより均一になります。
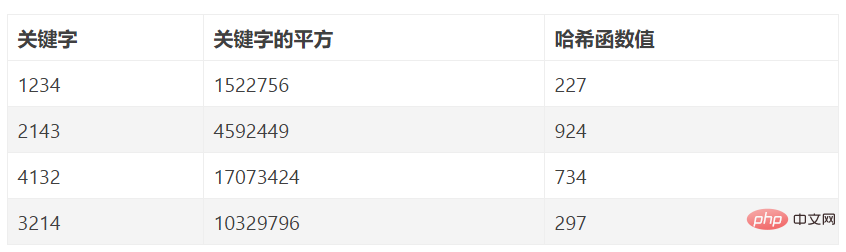
キーワードセット内の各キーワードは で構成されていると仮定します。 s 桁 (u1、u2、…、us) を使用して、キーワード セット全体を分析し、均等に分散されたいくつかのビットまたはその組み合わせをアドレスとして抽出します。デジタル解析手法は、データ要素キーワードの中で比較的均一な値を持ついくつかのデジタルビットをハッシュアドレスとして取得する手法です。つまり、キーワードの桁数が多い場合、キーワードのビットを分析し、不均一に分散したビットをハッシュ値として破棄できます。すべてのキーワード値がわかっている場合にのみ適しています。分布を分析することにより、キーワード値の範囲がより小さいキーワード値の範囲に変換されます。
例: データ要素数 n=80、ハッシュ長 m=100 のハッシュ テーブルを構築します。一般性を失わないように、ここでは分析用に 8 つのキーワードのみを示します。8 つのキーワードは次のとおりです:
K1=61317602 K2=61326875 K3=62739628 K4=61343634
K5=62706815 K6= 62774638 K7=61381262 K8=61394220
上記 8 つのキーワードを分析すると、キーワードの左から右に向かって 1 桁目、2 桁目、3 桁目、6 桁目の値が比較的集中していることがわかります。ハッシュアドレスのうち、残りの4ビット目、5ビット目、7ビット目、8ビット目は偶数値であり、そのうちの2ビットをハッシュアドレスとして選択できます。最後の 2 桁がハッシュ アドレスとして選択されたとすると、これら 8 つのキーワードのハッシュ アドレスは、2、75、28、34、15、38、62、20 となります。
この方法は、すべてのキーワードの各桁におけるさまざまな数字の出現頻度を事前に推定できる場合に適しています。
5. 基数変換方法
キー値を別の基数系の数値とみなして、元の基数に変換します。そして、そのうちのいくつかをハッシュ アドレスとして選択します。
例 Hash(80127429)=(80127429)13=8137 0136 1135 2134 7133 4132 2*131 9=(502432641)10 中間の 3 桁をハッシュ値として取得すると、Hash(80127429) が得られます。 =432 良好なハッシュ関数を取得するには、最初に基数を変更し、次に折り畳んだり二乗したりするなど、いくつかの方法を組み合わせて使用できます。ハッシュが均一である限り、自由に組み合わせることができます。
6. 折り方
#キーコードの桁数が多く、四角中心の折り方が複雑な場合もありますが、キーコードを同じ桁数でいくつかの部分に分割し(最後の部分の桁数は異なっていてもよい)、それらの部分を重ね合わせた合計(実行)をハッシュアドレスとします。この方法を折り曲げ法といいます。
は次のように分割されます。
シフト重ね合わせ:分割された部分の下位ビットを位置合わせして加算します。 境界線オーバーレイ: 分割境界に沿って一方の端から前後に折り、位置を合わせて追加します。
3. 競合解決戦略
ハッシュ関数の目的は競合を最小限に抑えることですが、実際には競合は避けられません。したがって、私たちは紛争解決戦略を検討する必要があります。競合解決技術は、オープン ハッシュ (ジッパー方式、セパレート チェーンとも呼ばれます) とクローズド ハッシュ方式 (クローズド ハッシュ、オープン アドレス方式、オープン アドレス指定とも呼ばれます) の 2 つのカテゴリに分類できます。これら 2 つのメソッドの違いは、オープン ハッシュ メソッドは衝突するキーをメイン ハッシュ テーブルの外に保存するのに対し、クローズド ハッシュ メソッドは衝突するキーをテーブル内の別のスロットに保存することです。
1. 分離リンクリスト方式
(1)ジッパー方式
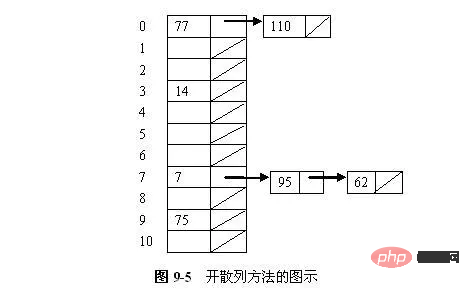
ハッシュ方式の一種単純な形式は、ハッシュ テーブル内の各スロットをリンク リストの先頭として定義することです。特定のスロットにハッシュされるすべてのレコードは、そのスロットのリンク リストに追加されます。図 9-5 は、各スロットにレコードとリンク リストの残りの部分へのポインタが格納されるオープン ハッシュ テーブルを示しています。これら 7 つの数値は 11 スロットを持つハッシュ テーブルに格納され、使用されるハッシュ関数は h(K) = K mod 11 です。番号の挿入順序は、77、7、110、95、14、75、62 です。スロット 0 にハッシュされた値が 2 つ、スロット 3 にハッシュされた値が 1 つ、スロット 7 にハッシュされた値が 3 つ、スロット 9 にハッシュされた値が 1 つあります。
2. クローズド ハッシュ法 (オープン アドレス法)
クローズド ハッシュ法は、すべてのレコードを結合します。ハッシュ テーブルに直接保存されます。各レコードキー key は、ハッシュ関数によって計算されたベース位置、つまり h(key) を持ちます。キーが挿入されるときに、別のレコードがすでに R のベース位置を占めている場合 (衝突が発生した場合)、R はテーブル内の別のアドレスに格納され、競合解決ポリシーによってそのアドレスが決定されます。
クローズド ハッシュ テーブルの競合解決の基本的な考え方は、競合が発生した場合、特定の方法を使用して、ハッシュ アドレス シーケンス d0、d1、d2、...di、...dm を生成します。キー K -1。このうち、d0=h(K)はKのベースアドレスホームポジションと呼ばれ、すべてのdi(0<i<m)は後続のハッシュアドレスである。 K が挿入されるとき、ベース アドレスのノードがすでに他のデータ要素によって占有されている場合、そのノードは上記のアドレス シーケンスに従って順番にプローブされ、最初に見つかった開いている空き位置 di が K の格納場所として使用されます。 ; 後続のすべてのハッシュに空きアドレスがない場合は、閉じられたハッシュ テーブルがいっぱいで、オーバーフローが報告されることを示します。同様に、K を取得する場合、同じ値を持つ後続アドレスのシーケンスが順番に検索され、取得が成功すると位置 di が返されます。プローブ シーケンスに沿って取得するときに開いている空きアドレスが見つかった場合は、それが意味します。テーブルコード内に検索対象のキーが存在しないことを示します。 K を削除するときは、同じ値を持つ後続アドレスのシーケンスに従って順次検索し、特定の位置 di に K 値があることがわかったら、位置 di のデータ要素を削除します (削除操作は実際には、単にデータ要素をマークするだけです)。削除用のノード); 開いている空きアドレスが見つかった場合は、テーブル内に削除するキーがないことを意味します。したがって、閉じられたハッシュ テーブルの場合、後続のハッシュ アドレスのシーケンスを構築する方法が競合を処理する方法になります。
プローブを作成する方法が異なると、競合を解決する方法も異なります。以下にいくつかの一般的な構築方法を示します。
(1) 線形検出方式
ハッシュテーブルをリングテーブルとして扱い、ベースアドレスdで競合が発生した場合(例: h(K)=d) ) の場合、空きアドレスが見つかるか、キー コードが見つかるまで、次のアドレス単位が順番に探索されます: d 1、d 2、...、M-1、0、1、...、d-1キーのノード。もちろん、プローブシーケンスに沿って検索した後にアドレス d に戻った場合、挿入操作を実行しているか、取得操作を実行しているかに関係なく、失敗を意味します。単純な線形プローブのプローブ関数は次のとおりです: p(K,i) = i
例 9.7 キー コードのセットは (26, 36, 41, 38, 44, 15, 68, 12, 06, 51, 25)、ハッシュ テーブルの長さ M = 15、および線形探索法は、このキーのセットの競合構造ハッシュ テーブルを解決するために使用されます。 n=11 であるため、剰余メソッドを使用してハッシュ関数を作成し、M より小さい最大の素数 P=13 を選択します。この場合、ハッシュ関数は次のようになります: h(key) = key。各ノードを次の順序で挿入します。 26: h(26) = 0、36: h(36) = 10、41: h(41) = 2、38: h(38) = 12、44: h(44) = 5 。 15 が挿入されると、そのハッシュ アドレスは 2 になります。2 はキー コード 41 の要素によってすでに占有されているため、プローブする必要があります。シーケンシャルプローブ法によれば、3 はオープンフリーアドレスであることが明らかなので、ユニット 3 に配置できます。同様に、ユニット 4 に 68 を、ユニット 13 に 12 を配置することができます。 : 生成された後続のハッシュ アドレスは連続していませんが、後続のデータ要素のための余地を残すためにスキップされ、集計が削減されます。二次検出方法の検出シーケンスは、12、-12、22、-22、... などです。つまり、競合が発生すると、最初のアドレスの両端で同義語が前後にハッシュされます。次の空きアドレスを見つけるための式は次のとおりです。


たとえば、既知のハッシュ テーブルの長さ m=11 の場合、ハッシュ関数は次のようになります: H (key) = key % 11, then H (47) = 3, H ( 26)=4、H(60)=5、次のキーワードが 69 であると仮定すると、H(69)=3 となり、47 と競合します。線形検出とハッシュを使用して競合を処理する場合、次のハッシュ アドレスは H1=(3 1)% 11 = 4 ですが、依然として競合が存在します。その後、次のハッシュ アドレスは H2=(3 2)% 11 であることがわかります。 = 5、まだ競合がある場合は、H3 = (3 3)% 11 = 6 として次のハッシュ アドレスの検索を続けます。この時点では競合はありません。ユニット 5 に 69 を入力します。図 8.26 (a) を参照してください。 。二次検出とハッシュを使用して競合を処理する場合、次のハッシュ アドレスは H1=(3 12)% 11 = 4 になります。それでも競合がある場合は、次のハッシュ アドレス H2=(3 - 12)% 11 = 2 を見つけます。 、現時点では競合はありません。ユニット 2 に 69 を入力します (図 8.26 (b) を参照)。競合を処理するために擬似乱数検出とハッシュが使用され、擬似乱数シーケンスが 2、5、9、……の場合、次のハッシュ アドレスは H1 = (3 2)% 11 = 5 になります。 , そしてまだ競合があります。次のハッシュ アドレスを H2 = (3 5)% 11 = 8 として見つけます。この時点では競合はありません。ユニット 8 に 69 を入力します (図 8.26 (c) を参照)。
(4)二重ハッシュ検出方法擬似ランダム プローブと二次プローブはどちらも、基本的な集約の問題、つまり、異なるベース アドレスを持つキー コードと、それらのプローブ シーケンスの一部のセグメントが重複する問題を排除できます。ただし、2 つのキーが同じベース アドレスにハッシュされた場合、両方の方法を使用して同じプローブ シーケンスが取得され、依然として集約が発生します。これは、擬似ランダム プローブとセカンダリ プローブによって生成されるプローブ シーケンスはベース アドレスのみの関数であり、元のキー値の関数ではないためです。この問題は二次クラスタリングと呼ばれます。
二次集約を回避するには、探索シーケンスをベース位置の関数ではなく、元のキー値の関数にする必要があります。ダブルハッシュ検出法は、2 番目のハッシュ関数を定数として使用し、定数項を毎回スキップして線形検出を行います。
以上が毎日使ってください! HASHって知っていますか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

