
1. 因果推論の研究パラダイム
研究パラダイムには現在 2 つの主要な研究方向があります:
- Judea Pearl 構造モデル
- 潜在的な出力フレームワーク

ジューデア・パール著『The Book of Why – The New Science of Cause and Effect』では、この本では次のように述べています。認知ラダーは 3 つのレベルとして配置されています:
- 最初のレベル - 相関関係: 相関関係を通じてルールを見つけます。直接観察できます。
- 第 2 レベル - 介入: 現状が変更された場合、どのようなアクションを実行する必要があり、どのような結論を導き出す必要があるかは、実験を通じて観察できます。
- #第 3 レベル - 反事実: 法律や規制などの問題により、実験的に直接観察することはできません。それをどう評価するか ATE と CATE はさらに難しい問題です。

1. 原因と結果関連#: 原因と結果の間には、信頼性があり、追跡可能で、確実に依存する関係があります。たとえば、煙と煙警報器には因果関係があります。
2. 混同された相関関係 #: 身長と読解力に関連性があるかどうかなど、直接観察できない交絡変数が含まれています。変数の年齢は類似しているため、有効な結論が導き出されます;
3. 選択バイアス: 本質的にバークソンのパラドックスは、たとえば、外見と才能の関係を調査する場合、有名人の間でのみ観察すると、外見と才能が両方を持つことはできないという結論に達する可能性があります。全人類で観察した場合、容姿と才能の間には因果関係はありません。
4. 逆因果関係 #: つまり、原因と結果の逆転です。たとえば、統計は次のようになります。人間は結婚生活が長くなればなるほど、平均余命は長くなります。しかし逆に、「長生きしたければ早く結婚しなければならない」とは言えません。
#交絡因子が観察結果にどのような影響を与えるかを、ここで 2 つのケースで説明します。

上の図は、運動量とコレステロール値の関係を示しています。左の図から、運動量が多いほどコレステロール値が高いと結論付けることができます。しかし、年齢層別を加えると、同じ年齢層別では運動量が多いほどコレステロール値は低下する。さらに、加齢とともにコレステロール値は徐々に上昇するため、この結論は私たちの知識と一致しています。

2 番目の例は、信用シナリオです。過去の統計から、所定の限度額(借入可能額)が高くなるほど延滞率が低くなることがわかります。ただし、金融分野では、まず借り手の信用度が A カードに基づいて判断され、信用度が高ければ、プラットフォームはより高い限度額を付与し、全体的な延滞率は非常に低くなります。しかし、ローカルでのランダム実験によると、同じ与信資格を持つ人々であっても、与信限度額移行曲線の変化が緩やかな人もいる一方、与信限度額移行リスクがより高い人もいる。増加すると、リスクの増加が大きくなります。
上記の 2 つのケースは、モデリングで交絡因子が無視された場合、誤った結論、さらには反対の結論が得られる可能性があることを示しています。

RCT ランダムサンプルから観察サンプル因果モデリングに移行するにはどうすればよいですか?
RCT サンプルの場合、ATE 指標を評価したい場合は、グループ減算または DID (差分の差) を使用できます。 CATE インジケーターを評価したい場合は、隆起モデリングを使用できます。一般的な手法には、メタ学習器、二重機械学習、コーサル フォレストなどが含まれます。ここで注意すべき 3 つの前提条件があります。SUTVA、混乱のなさ、積極性です。中心となる仮定は、観察されていない交絡因子は存在しないということです。
観察サンプルのみの場合、治療→結果の因果関係を直接求めることはできません。共変量から治療へのバックドアパス。一般的な方法は、操作変数法と反事実表現学習です。操作変数手法では、具体的なビジネスの詳細を剥ぎ取り、ビジネス変数の因果関係図を描く必要があります。反事実表現学習は、成熟した機械学習に依存して、因果関係の評価のために類似の共変量を持つサンプルを照合します。
#2. 因果推論のフレームワークの進化
1. ランダムデータから観察データへ
## 次に、因果推論のフレームワークの進化と、因果表現の学習に段階的に移行する方法を紹介します。
#一般的な Uplift モデルには、Slearner、Tlearner、Xlearner が含まれます。
#ここで、Slearner は介在する変数を 1 次元の特徴として扱います。一般的なツリー モデルでは、治療が容易に圧倒され、治療効果の推定値が小さくなることに注意してください。

#Tlearner は治療を離散化し、グループ内の介在変数をモデル化し、各治療の予測モデルを構築して、違いがございます。サンプルサイズが小さいほど、推定される分散が大きくなることに注意することが重要です。

X学習者グループのクロスモデリングでは、実験グループと対照グループが個別に相互計算され、トレーニングされます。この方法は S/T-learner の利点を組み合わせていますが、欠点は、高次モデルの構造エラーが発生し、パラメーター調整の難易度が高くなるということです。

3 つのモデルの比較:

上図の横軸は複合因果効果とMSEの推定誤差、縦軸は単純因果効果、横軸と縦軸はMSEの推定誤差です。軸はそれぞれ 2 つの部分のデータを表します。緑色は Slearner の誤差分布、茶色は Tlearner の誤差分布、青色は Xlearner の誤差分布を表します。 ランダムなサンプル条件下では、Xlearner は複雑な因果効果の推定と単純な因果効果の推定の両方に優れています。Slearner は複雑な因果効果の推定では比較的パフォーマンスが悪く、単純な因果効果の推定には優れています。トレーナーはスラーナーの反対です。 
# ランダムなサンプルがある場合は、X から T までの矢印を削除できます。観察モデリングに移行した後は、X から T への矢印を取り除くことはできず、治療と転帰は同時に交絡因子の影響を受けることになりますが、このとき、何らかの脱分極処理を行うことができます。例えば、DML (Double Machine Learning) 手法は 2 段階のモデリングを実行します。最初の段階では、X はユーザー自身の表現特性 (年齢、性別など) です。交絡変数には、たとえば、特定のグループの人々を選別するためのこれまでの取り組みが含まれる可能性があります。第 2 段階では、前段階の計算結果の誤差がモデル化されます。これが CATE の推定値です。
ランダム データから観測データまで 3 つの処理方法があります。
(1 ) ランダム化実験を実施するが、ビジネスコストが高い;
(2) 操作変数を見つけるのは一般に困難;
(3) すべての交絡因子が観察されたと仮定して、DML、表現学習、およびその他の方法を使用して、類似したサンプルを照合します。
2. 因果表現の学習

中心となるアイデア反事実学習 さまざまな処理の下で特徴分布のバランスをとることです。
核心的な質問は 2 つあります:1. トレーニング サンプルの重みを調整するにはどうすればよいですか?
#2. 変換されたサンプルを表現空間内の実験グループと対照グループにさらに均等に分散させるにはどうすればよいでしょうか?
#本質的なアイデアは、変換マッピング後に各サンプルの反事実的な「双子」を見つけることです。マッピング後、治療グループと対照グループの X の分布は比較的類似しています。

より代表的な研究は、TKDE 2022 に掲載された論文で、DeR-CFR の一部の研究を紹介しています。この部分はこれは実際には DR-CRF モデルの反復であり、モデルフリーの方法を使用して観測変数を分離します。
# X 変数を調整変数 A、操作変数 I、交絡変数 C の 3 つの部分に分割します。次に、I、C、A を使用してさまざまな処理の下で X の重みを調整し、観察されたデータの因果モデリングの目的を達成します。
#この方法の利点は、交絡因子を分離し、推定のバイアスを軽減できることです。欠点は、継続的な介入に対処するのが難しいことです。
#このネットワークの核心は、3 種類の変数 A/I/C をどのように分離するかです。調整変数 A は Y のみに関連しており、A と T が直交し、A から Y までの経験的誤差が小さいことを保証する必要があります。操作変数 I は T のみに関連しており、次の条件を満たす必要があります。 T に関する I と Y の条件付き独立性、および T に関する I の経験 誤差は小さい; 混同変数 C は T と Y の両方に関連しており、w はネットワークの重みです。重みを考慮するには、C と T が w に関して条件付きで独立していることを確認する必要があります。ここでの直交性は、対数損失や mse ユークリッド距離などの一般的な距離公式やその他の制約によって実現できます。

また、継続的介入に対処する方法に関する新しい論文研究もいくつかあり、ICLR2021 で公開された VCNet では、継続的介入の推定方法が提供されています。欠点は、観測データ(CFRシナリオ)に直接適用することが難しいことです。
マップ 寄与する変数は X から抽出されます。ここでは、連続処理を B 分割/予測ヘッドに分割し、各連続関数を分割線形関数に変換し、経験的誤差対数損失を最小化して
# # を学習します。 
# 次に、学習した Z と θ(t) を使用します。  それが結果です。ここでの θ(t) が連続処理の鍵となるのですが、可変係数モデルではありますが、このモデルは連続処理のみを扱っているため、観測データの場合、各 B セグメントのデータが均一であることは保証できません。
それが結果です。ここでの θ(t) が連続処理の鍵となるのですが、可変係数モデルではありますが、このモデルは連続処理のみを扱っているため、観測データの場合、各 B セグメントのデータが均一であることは保証できません。
3. 反事実的なクォータ モデル Mono-CFR
最後に、Du Xiaoman の反事実を紹介しましょう。信用モデルは主に、観察データに対する継続的治療の反事実推定の問題を解決します。

#核心的な問題は、プラットフォームの利益を最大化するためにユーザーの (借入可能な) クォータをどのように設計するかということです。ここでの先験的な知識は、限度額が高いほど、より多くのユーザーが借りることになり、デフォルトのリスクが高まるということです。逆に。
- #最初のステップは、利益計算式を定義することです。利益 = 割り当て収入 - 割り当てリスク。計算式は単純そうに見えますが、実際には調整すべき点がたくさんあります。このようにして、問題は、観察データに基づいて、割り当てとリスク(不良債権)、割り当てと収入の間の因果関係をモデル化することに変換されます。
- #2 番目のステップは、各割り当てレベルでのユーザーの推定収入と不良債権を推定し、最大利益額を決定することです。
各ユーザーは、上の図に示すような利益曲線を持つことが期待されます。さまざまな割り当てレベルでは、収入の値は事実の推定に反比例します。

#観測データで、量が多ければ多いほどリスクが低いことがわかります。これは本質的に次のような理由によるものです。交絡因子の存在。私たちのシナリオで混乱を招く要因は、信用資格です。良好な信用資格を持つ人に対しては、プラットフォームはより高い限度額を付与し、その逆の場合は、プラットフォームはより低い限度額を付与します。優れた信用資格を持つ人々の絶対リスクは、低い信用資格を持つ人々の絶対リスクよりも依然として大幅に低いです。信用資格を向上させると、限度額の引き上げがリスクの増加をもたらし、限度額の上限がユーザー自身の支払い能力を超えることがわかります。

モデルのアイデア: 期待量 μ(T|X) が与えられた場合、ΔT と Y の間の単調関係 (用量反応曲線) を学習します。期待量はモデルに学習された連続的な傾向量として理解できるため、交絡変数Cと量Tの関係を切り離してΔTとYの因果関係学習に変換し、分布を比較することができます。 ΔT の下での Y の良好な特性評価。

#ここでは、上記の抽象フレームワークをさらに洗練させます。 ΔT を可変係数モデルに変換し、IntegrandNN ネットワークに接続します。トレーニング エラーは 2 つの部分に分割されます:

#ここでの α は、リスクの重要性を測定するハイパーパラメータです。
Mono-CFR は 2 つの部分で構成されます:
- クォータ傾向ネットワーク:X⊥ΔTとなるように戦略傾向量を予測します。
関数 1: T に最も関連する X 内の変数を抽出し、経験的誤差を最小限に抑えます。
# 機能 2: 過去の戦略に近似サンプルを固定します。
- リスク単調ネットワーク: 制約 ΔT と Y の間の理論的な単調関係。
#機能 2: 推定バイアスを軽減します。
問題は次のように変換されます:
- 割り当て傾向ネットワーク: 検証出力 Δ T と Y の関係。
- リスク単調ネットワーク: ΔT と Y の単調性を制限するにはどうすればよいですか?
- #実際の金額傾向ネットワークの入力は次のとおりです:
 #横軸はAカードスコアで定義されるグループであり、異なる傾向のノルマμ(T|X)の下で、ノルマの差ΔTと延滞率が変化していることがわかります。 Yは単調増加の関係を示しており、グループの質が低いほど信用差ΔTの変化曲線が急峻になり、実際の延滞率の変化曲線も急峻になり、全体の傾きが大きくなる。ここでの結論は、すべて履歴データの学習を通じて導き出されます。
#横軸はAカードスコアで定義されるグループであり、異なる傾向のノルマμ(T|X)の下で、ノルマの差ΔTと延滞率が変化していることがわかります。 Yは単調増加の関係を示しており、グループの質が低いほど信用差ΔTの変化曲線が急峻になり、実際の延滞率の変化曲線も急峻になり、全体の傾きが大きくなる。ここでの結論は、すべて履歴データの学習を通じて導き出されます。
 X 分布図と ΔT 分布図からわかります: さまざまな条件人々の集団間の差ΔT(図では色で区別)が同じ間隔で均等に分布していることを、実践的な観点から説明します。
X 分布図と ΔT 分布図からわかります: さまざまな条件人々の集団間の差ΔT(図では色で区別)が同じ間隔で均等に分布していることを、実践的な観点から説明します。

#理論的な観点からは、厳密に証明することもできます。
2 番目の部分は、リスク単調ネットワークの実装です:

ここでの ELU 1 関数の数式は次のとおりです:


##ΔT と延滞率は単調増加傾向を示し、これは ELU 1 関数の導関数が常に または より大きいことで保証されます。 0に等しい。
以下では、リスク単調ネットワークが弱い係数変数をより正確に学習する方法を説明します:
次のような数式があるとします。

が表示されます。ここで ##xx1 は弱い係数変数です。x1## に単調性を適用する場合# 性的拘束の後、応答 Y の推定はより正確になります。このような個別の制約がないと、#1 の重要性が #2 に圧倒され、その結果、モデルのバイアスが増加します。
 #オフラインで金額のリスク推定曲線を評価するにはどうすればよいですか?
#オフラインで金額のリスク推定曲線を評価するにはどうすればよいですか?
は 2 つの部分に分かれています:
パート 1: 解釈可能な検証

#パート 2: 小規模なトラフィック実験を使用して、さまざまな増加範囲でのリスク偏差が上昇値ビニングを通じて取得できることを検証します。
- ##オンライン実験の結論:
条件は、ノルマが30%増加、利用者の延滞額が20%以上減少、借入が30%増加、収益性が30%以上増加すること。
将来のモデルの期待:
モデルフリー形式で操作変数と調整を組み合わせる変数がより明確に分離されるため、劣等集団に対するリスク移転においてモデルのパフォーマンスが向上します。
実際のビジネス シナリオでは、Du Xiaoman のモデル進化の反復プロセスは次のとおりです:

#最初のステップは観察モデリングであり、過去の観察データを継続的にスクロールし、反事実的因果学習を実行し、新しいトレーニング ウィンドウを常に開きます。外部データソースによって補完されます。
#2 番目のステップはモデルの反復です。効果は、効果的なモデルの反復をサポートするために、少量のトラフィックのランダム サンプルに基づいて検証されます。
#3 番目のステップはビジネス上の意思決定であり、ビジネスはモデルの出力に基づいて実験的な意思決定を行い、モデル効果の向上を検証し、ビジネス上の利益を獲得します。
以上が反事実的因果推論に基づく Duxiaoman クォータ モデルの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 AIのスキルギャップは、サプライチェーンのダウンを遅くしていますApr 26, 2025 am 11:13 AM
AIのスキルギャップは、サプライチェーンのダウンを遅くしていますApr 26, 2025 am 11:13 AM「AI-Ready労働力」という用語は頻繁に使用されますが、サプライチェーン業界ではどういう意味ですか? サプライチェーン管理協会(ASCM)のCEOであるAbe Eshkenaziによると、批評家ができる専門家を意味します
 1つの会社がAIを永遠に変えるために静かに取り組んでいる方法Apr 26, 2025 am 11:12 AM
1つの会社がAIを永遠に変えるために静かに取り組んでいる方法Apr 26, 2025 am 11:12 AM分散型AI革命は静かに勢いを増しています。 今週の金曜日、テキサス州オースティンでは、ビテンサーのエンドゲームサミットは極めて重要な瞬間を示し、理論から実用的な応用に分散したAI(DEAI)を移行します。 派手なコマーシャルとは異なり
 Nvidiaは、AIエージェント開発を合理化するためにNEMOマイクロサービスをリリースしますApr 26, 2025 am 11:11 AM
Nvidiaは、AIエージェント開発を合理化するためにNEMOマイクロサービスをリリースしますApr 26, 2025 am 11:11 AMエンタープライズAIはデータ統合の課題に直面しています エンタープライズAIの適用は、ビジネスデータを継続的に学習することで正確性と実用性を維持できるシステムを構築する大きな課題に直面しています。 NEMOマイクロサービスは、NVIDIAが「データフライホイール」と呼んでいるものを作成することにより、この問題を解決し、AIシステムがエンタープライズ情報とユーザーインタラクションへの継続的な露出を通じて関連性を維持できるようにします。 この新しく発売されたツールキットには、5つの重要なマイクロサービスが含まれています。 NEMOカスタマイザーは、より高いトレーニングスループットを備えた大規模な言語モデルの微調整を処理します。 NEMO評価者は、カスタムベンチマークのAIモデルの簡素化された評価を提供します。 Nemo Guardrailsは、コンプライアンスと適切性を維持するためにセキュリティ管理を実装しています
 aiは芸術とデザインの未来のために新しい絵を描きますApr 26, 2025 am 11:10 AM
aiは芸術とデザインの未来のために新しい絵を描きますApr 26, 2025 am 11:10 AMAI:芸術とデザインの未来 人工知能(AI)は、前例のない方法で芸術とデザインの分野を変えており、その影響はもはやアマチュアに限定されませんが、より深く影響を与えています。 AIによって生成されたアートワークとデザインスキームは、広告、ソーシャルメディアの画像生成、Webデザインなど、多くのトランザクションデザインアクティビティで従来の素材画像とデザイナーに迅速に置き換えられています。 ただし、プロのアーティストやデザイナーもAIの実用的な価値を見つけています。 AIを補助ツールとして使用して、新しい美的可能性を探求し、さまざまなスタイルをブレンドし、新しい視覚効果を作成します。 AIは、アーティストやデザイナーが繰り返しタスクを自動化し、さまざまなデザイン要素を提案し、創造的な入力を提供するのを支援します。 AIはスタイル転送をサポートします。これは、画像のスタイルを適用することです
 エージェントAIとのズームがどのように革命を起こしているか:会議からマイルストーンまでApr 26, 2025 am 11:09 AM
エージェントAIとのズームがどのように革命を起こしているか:会議からマイルストーンまでApr 26, 2025 am 11:09 AM最初はビデオ会議プラットフォームで知られていたZoomは、エージェントAIの革新的な使用で職場革命をリードしています。 ZoomのCTOであるXD Huangとの最近の会話は、同社の野心的なビジョンを明らかにしました。 エージェントAIの定義 huang d
 大学に対する実存的な脅威Apr 26, 2025 am 11:08 AM
大学に対する実存的な脅威Apr 26, 2025 am 11:08 AMAIは教育に革命をもたらしますか? この質問は、教育者と利害関係者の間で深刻な反省を促しています。 AIの教育への統合は、機会と課題の両方をもたらします。 Tech Edvocate NotesのMatthew Lynch、Universitとして
 プロトタイプ:アメリカの科学者は海外の仕事を探していますApr 26, 2025 am 11:07 AM
プロトタイプ:アメリカの科学者は海外の仕事を探していますApr 26, 2025 am 11:07 AM米国における科学的研究と技術の開発は、おそらく予算削減のために課題に直面する可能性があります。 Natureによると、海外の雇用を申請するアメリカの科学者の数は、2024年の同じ期間と比較して、2025年1月から3月まで32%増加しました。以前の世論調査では、調査した研究者の75%がヨーロッパとカナダでの仕事の検索を検討していることが示されました。 NIHとNSFの助成金は過去数か月で終了し、NIHの新しい助成金は今年約23億ドル減少し、3分の1近く減少しました。リークされた予算の提案は、トランプ政権が科学機関の予算を急激に削減していることを検討しており、最大50%の削減の可能性があることを示しています。 基礎研究の分野での混乱は、米国の主要な利点の1つである海外の才能を引き付けることにも影響を与えています。 35
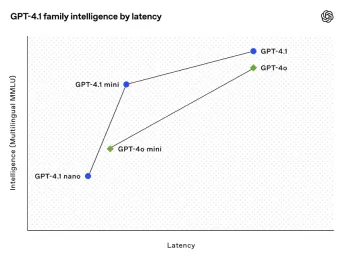 オープンAIの最新のGPT 4.1ファミリ - 分析VidhyaApr 26, 2025 am 10:19 AM
オープンAIの最新のGPT 4.1ファミリ - 分析VidhyaApr 26, 2025 am 10:19 AMOpenaiは、強力なGPT-4.1シリーズを発表しました。実際のアプリケーション向けに設計された3つの高度な言語モデルのファミリー。 この大幅な飛躍は、より速い応答時間、理解の強化、およびTと比較した大幅に削減されたコストを提供します


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

EditPlus 中国語クラック版
サイズが小さく、構文の強調表示、コード プロンプト機能はサポートされていません

AtomエディタMac版ダウンロード
最も人気のあるオープンソースエディター

MinGW - Minimalist GNU for Windows
このプロジェクトは osdn.net/projects/mingw に移行中です。引き続きそこでフォローしていただけます。 MinGW: GNU Compiler Collection (GCC) のネイティブ Windows ポートであり、ネイティブ Windows アプリケーションを構築するための自由に配布可能なインポート ライブラリとヘッダー ファイルであり、C99 機能をサポートする MSVC ランタイムの拡張機能が含まれています。すべての MinGW ソフトウェアは 64 ビット Windows プラットフォームで実行できます。

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SecLists
SecLists は、セキュリティ テスターの究極の相棒です。これは、セキュリティ評価中に頻繁に使用されるさまざまな種類のリストを 1 か所にまとめたものです。 SecLists は、セキュリティ テスターが必要とする可能性のあるすべてのリストを便利に提供することで、セキュリティ テストをより効率的かつ生産的にするのに役立ちます。リストの種類には、ユーザー名、パスワード、URL、ファジング ペイロード、機密データ パターン、Web シェルなどが含まれます。テスターはこのリポジトリを新しいテスト マシンにプルするだけで、必要なあらゆる種類のリストにアクセスできるようになります。

ホットトピック
 7737
7737 15
15 1643
1643 14
14 1397
1397 52
52 1290
1290 25
25 1233
1233 29
29



