Javaで二分探索木を実装する方法

1. 概念

a. これはバイナリ ツリーです (各ノードには最大 2 つの子ノードがあります)

b. このツリー内のノードのノード値については

左側のサブツリーのすべてのノード値

二分探索木では、一般に値が等しい状況は起こりません。 JDK の検索ツリーには同じ値 (TreeMap-key) が存在しない

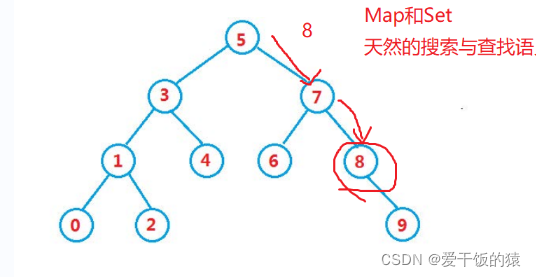
#最大の特徴: を検索する方法でもあります。検索ツリーであるかどうかを判断します。

ツリーを順番に走査すると、昇順集合 0 1 2 3 4 5 6 7 8 9

バイナリの時間計算量が得られます。順序付けられた間隔で検索しますか? logn は logN まで /2/2/2 ==1 を設定し続けます

#logN =>>「木」を考えてください

2. キー操作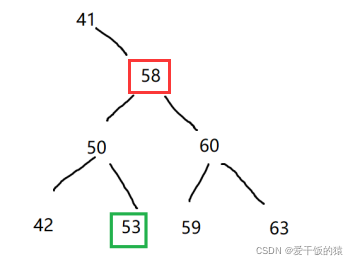

58 が削除されると、このノードの左右のサブツリーの両方が空になりません

Hibbard 削除 1962

両方を持つ BST のノードを削除します左右のサブツリー

削除としてルート ノードとして 58 を持つ先行ノードまたは後続ノードを検索します。

先行ノードの後の新しいノード: 58 をルートとする BST 内の 58 未満の最後のノード - >53

後続ノード: 58 をルートとする BST 内の 58 より大きい最初のノード Node 58->59

後続ノードを使用する場合は、最初にremoveMin(root.right) を接続します。次に、root.left

TreeNode successor = findMin(root.right);
successor.right = removeMin(root.right);
successor.left = root.left;

3 に接続します。完全なコード

import java.util.NoSuchElementException;
 
/**
 * 基于整型的
 * 普通的二分搜索树
 */
public class BST {
 
    private class TreeNode{
        private int val;
        private TreeNode left;
        private TreeNode right;
 
        public TreeNode(int val) {
            this.val = val;
        }
    }
 
    private int size;
    private TreeNode root;
 
    /**
     * 向以root为根的BST中插入一个新的结点val
     * @param val
     */
    public void add(int val){
        root = add(root,val);
    }
 
    private TreeNode add(TreeNode root, int val) {
        if(root == null){
            //创建一个新节点
            TreeNode newNode = new TreeNode(val);
            size++;
            return newNode;
        }
        //左子树插入
        if(val < root.val){
            root.left = add(root.left,val);
        }
        //右子树插入
        if(val > root.val){
            root.right = add(root.right,val);
        }
        return root;
    }
 
    /**
     * 判断当前以root为根的BST中是否包含了val
     * @param val
     * @return
     */
    public boolean contains(int val){
        return contains(root,val);
    }
 
    private boolean contains(TreeNode root, int val) {
        if(root == null){
            return false;
        }
        if(val == root.val){
            //找到了
            return true;
        }else if(val < root.val){
            //递归左子树查找
            return contains(root.left,val);
        }else{
            //递归右子树查找
            return contains(root.right,val);
        }
    }
 
    /**
     * 找到最小值
     * @return
     */
    public int findMin(){
        //判空
        if(root == null){
            //抛出一个空指针异常
            throw new NoSuchElementException("root is empty! cannot find min");
        }
        TreeNode minNode = findMin(root);
        return minNode.val;
    }
 
    private TreeNode findMin(TreeNode root) {
        //当此节点左子树为空，说明此节点是最小值
        if(root.left == null){
            return root;
        }
        //递归访问左子树
        return findMin(root.left);
    }
 
    /**
     * 找到最大值
     * @return
     */
    public int findMax(){
        //判空
        if(root == null){
            throw new NoSuchElementException("root is empty! cannot find max");
        }
        TreeNode maxNode = findMax(root);
        return maxNode.val;
    }
 
    private TreeNode findMax(TreeNode root) {
        //当此节点右子树为空，说明此节点是最大值
        if(root.right == null){
            return root;
        }
        //递归访问右子树
        return findMax(root.right);
    }
 
    /**
     * 在当前BST中删除最小值节点，返回删除的最小值
     * @return
     */
    public int removeMin(){
        int min =findMin();
        root = removeMin(root);
        return min;
    }
 
    private TreeNode removeMin(TreeNode root) {
        if(root.left == null){
            TreeNode right = root.right;
            //找到最小值，删除节点
            root = root.left = null;
            size--;
            return right;
        }
        root.left = removeMin(root.left);
        return root;
    }
 
    /**
     * 在当前BST中删除最大值节点，返回删除的最大值
     * @return
     */
    public int removeMax(){
        int max = findMax();
        root = removeMax(root);
        return max;
    }
 
    //在当前以root为根的BST中删除最小值所在的节点，返回删除后的树根
    private TreeNode removeMax(TreeNode root) {
        if(root.right == null){
            TreeNode right = root.right;
            //找到最大值，删除节点
            root = root.right = null;
            size--;
            return right;
        }
        root.right = findMax(root.right);
        return root;
    }
 
    /**
     * 在当前以root为根节点的BST中删除值为val的节点
     * 返回删除后的新的根节点
     * @return
     */
    public void removeValue(int value){
        root = removeValue(root,value);
    }
 
    private TreeNode removeValue(TreeNode root, int value) {
        if(root == null){
            throw new NoSuchElementException("root is empty! cannot find remove");
        }else if(value < root.val){
            root.left = removeValue(root.left,value);
            return root;
        }else if(value > root.val){
            root.right = removeValue(root.right,value);
            return root;
        }else {
            //此时value == root.value
            if(root.left == null){
                //删除最小数
                TreeNode right = root.right;
                root = root.right = null;
                size--;
                return right;
            }
            if(root.right == null){
                //删除最大数
                TreeNode left = root.left;
                root = root.left =null;
                size--;
                return left;
            }
            //找到当前该删除节点的前驱或者后继节点作为删除后的新节点
            //当我们使用后继节点时，先连removeMin(root.right),在连root.left
            TreeNode successor = findMin(root.right);
            successor.right = removeMin(root.right);
            successor.left = root.left;
            return successor;
        }
    }
 
 
    @Override
    public String toString() {
        StringBuilder sb = new StringBuilder();
        generateBSTString(root,0,sb);
        return sb.toString();
    }
 
    //直观打印，可以看到树的深度
    private void generateBSTString(TreeNode root, int height, StringBuilder sb) {
        if(root == null){
            sb.append(generateHeightString(height)).append("NULL\n");
            return;
        }
        sb.append(generateHeightString(height)).append(root.val).append("\n");
        generateBSTString(root.left,height+1,sb);
        generateBSTString(root.right,height+1,sb);
    }
 
    private String generateHeightString(int height) {
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < height; i++) {
            sb.append("--");
        }
        return sb.toString();
    }
}

以上がJavaで二分探索木を実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。