ホームページ >Java >&#&チュートリアル >Java でトポロジーソートを実装する方法
Java でトポロジーソートを実装する方法
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB転載
- 2023-06-01 12:20:021493ブラウズ
伏線
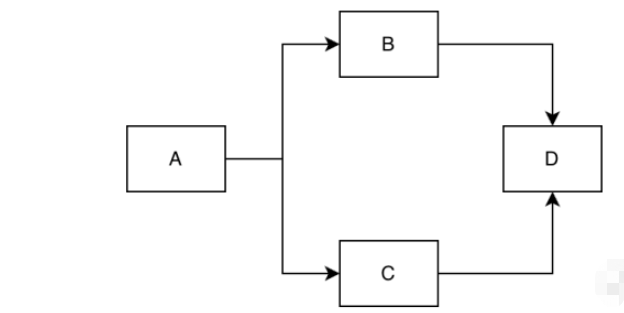
このセクションでは有向グラフに関連するアルゴリズムを紹介するため、最初に有向グラフの概念をいくつか説明します。これらの概念は後続の記事で説明されます。詳しくは説明されない。まず、有向グラフのノードを矢印付きの線で結びます。ノードの出力次数と入力次数を使用して説明できます。接続の末尾がノードを指している場合、出力次数は 1 ずつ増加し、接続の矢印がノードを指している場合、その入次数は 1 ずつ増加します。次の例を見てください。A の入力次数は 0 で出力次数は 2、B の入力次数は 1 と出力次数は 1、C の入力次数は 1 で出力次数は 1 です。次数が 1、D の入次数は 2、出次数は 0 です。
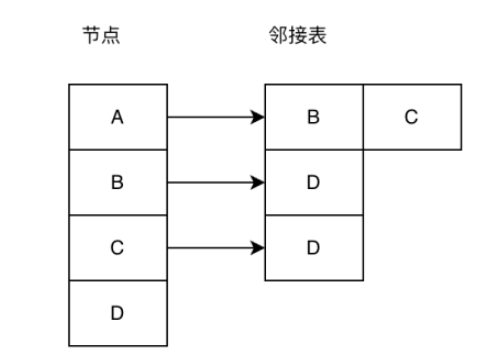
隣接リスト: 隣接リストは、グラフ構造を保存する効果的な方法です。下の図に示すように、左側のノード配列には、グラフ構造内のすべてのノードが保存されます。グラフ、右側の隣接リストにはノードが格納されます。
はじめに
この記事では、主にプリカーサーの問題を解決するための、有向非巡回グラフのアルゴリズムであるトポロジカルソートについて説明します。その後の関係、つまり現在の項目を完了するときに最初にどの項目を完了する必要があるかは、実際にプロセス管理でよく使用されます。下の図を見ると、最初に項目 A を完了する必要があり、その後、項目 B と C を完了できます。項目 B と C は並行していて順序がありませんが、項目 D は、項目 B と C が完了した後にのみ完了できます。トポロジカル ソートは、項目を完了するための合理的な順序を見つけるのに役立ちます。同時に、上の例を見てみましょう。項目 A が完了した後、項目 B と C は順序が異なります。B と C のどちらが先に完了しても、条件はが満たされるため、トポロジカルソートの順序は完全には確実ではありません。
作業プロセス
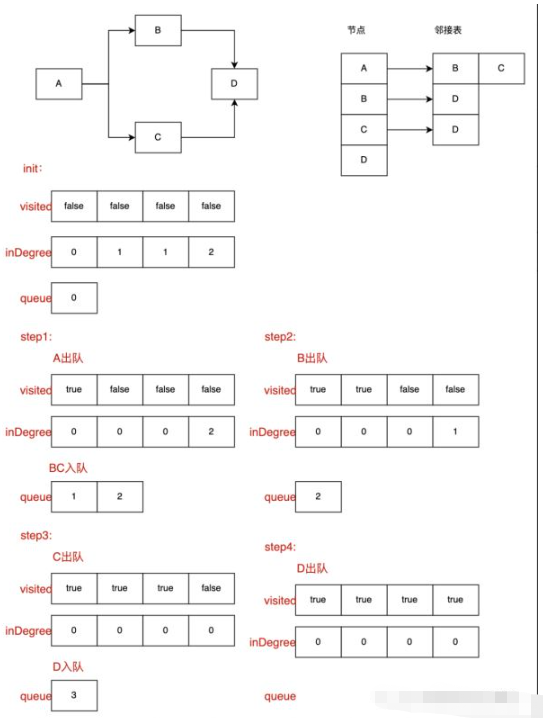
まず、トポロジカルソートに対応する演算は、有向非巡回グラフです。非巡回グラフの場合、入次数 0 のノードが少なくとも 1 つ存在する必要があります。現在の状況では、操作のために入次数 0 のノードを見つける必要があります。入次数 0 は、現在のノードに先行ノードがないか、先行ノードが処理されていて直接操作できることを意味します。操作が完了すると、現在のノードの後続ノードのすべての次数が 1 減らされ、次数ノードが 0 のノードが再度検索されて操作されます。現在の状況で入次数が 0 のノードは、すべてのノードが処理されるまで継続的に処理されます。
データ構造
以下は有向グラフの構造です。node は現在のグラフ内のすべてのノードを格納し、adj は対応するノードを格納します。隣接する点の添字ノード。グラフを初期化するときは、ノードの数を指定し、ノード配列と隣接配列を作成する必要があります。 addEdge という名前のメソッドを提供します。このメソッドは、2 つのノード間にエッジを確立する、つまり、先行ノードの隣接リストに後続ノードを追加するために使用されます。
public static class Graph{
/**
* 节点个数
*/
private Integer nodeSize;
/**
* 节点
*/
private char[] node;
/**
* 邻接表
*/
private LinkedList[] adj;
public Graph(char[] node) {
this.nodeSize = node.length;
this.node = node;
this.adj = new LinkedList[nodeSize];
for (int i = 0 ; i < adj.length ; i++) {
adj[i] = new LinkedList();
}
}
/**
* 在节点之间加边,前驱节点指向后继节点
* @param front 前驱节点所在下标
* @param end 后继节点所在下标
*/
public void addEdge(int front, int end) {
adj[front].add(end);
}
}トポロジカル ソート
トポロジカル ソートでは、最初に 2 つの一時配列、キュー、および inDegree 配列を初期化して、対応する添え字ノードの次数を格納します。これは、訪問する各ノードが先行ノードの次数を必要とするためです。ノードはすでに完了しています。つまり、入次数は 0 です。この配列を使用すると、これらのノードを比較的早く見つけることができます。もう 1 つは、複数の訪問を防ぐために現在のノードが訪問されているかどうかをマークする訪問済み配列です。キューは現在の状況で、次数 0 のすべてのノードに保存されます。 (アクセスの便宜上、ノードの添え字をすべて保存していることに注意してください。ステップ 1: inDegree 配列と訪問済み配列を初期化します。ステップ 2: inDegree 配列を走査し、inDegree 配列が 0 であるすべてのノードをノード キューに入れます。ステップ 3: ノードを終了します。キュー; 現在のノードが訪問済みかどうかを訪問済みに基づいて判断し、訪問済みの場合はステップ 3 に戻り、そうでない場合は次のステップに進みます; 現在のノードの隣接ノードの入次数を -1 に設定します、隣接ノードの入次数が 0 かどうかを判断し、0 の場合は直接ノード キューに入れ、0 でない場合はステップ 3 に戻ります;
/**
* @param graph 有向无环图
* @return 拓扑排序结果
*/
public List<Character> toPoLogicalSort(Graph graph) {
//用一个数组标志所有节点入度
int[] inDegree = new int[graph.nodeSize];
for (LinkedList list : graph.adj) {
for (Object index : list) {
++ inDegree[(int)index];
}
}
//用一个数组标志所有节点是否已经被访问
boolean[] visited = new boolean[graph.nodeSize];
//开始进行遍历
Deque<Integer> nodes = new LinkedList<>();
//将入度为0节点入队
for (int i = 0 ; i < graph.nodeSize; i++) {
if (inDegree[i] == 0) {
nodes.offer(i);
}
}
List<Character> result = new ArrayList<>();
//将入度为0节点一次出队处理
while (!nodes.isEmpty()) {
int node = nodes.poll();
if (visited[node]) {
continue;
}
visited[node] = true;
result.add(graph.node[node]);
//将当前node的邻接节点入度-1;
for (Object list : graph.adj[node]) {
-- inDegree[(int)list];
if (inDegree[(int)list] == 0) {
//前驱节点全部访问完毕,入度为0
nodes.offer((int) list);
}
}
}
return result;
}テスト サンプル 1
public static void main(String[] args) {
ToPoLogicalSort toPoLogicalSort = new ToPoLogicalSort();
//初始化一个图
Graph graph = new Graph(new char[]{'A', 'B', 'C', 'D'});
graph.addEdge(0, 1);
graph.addEdge(0,2);
graph.addEdge(1,3);
graph.addEdge(2,3);
List<Character> result = toPoLogicalSort.toPoLogicalSort(graph);
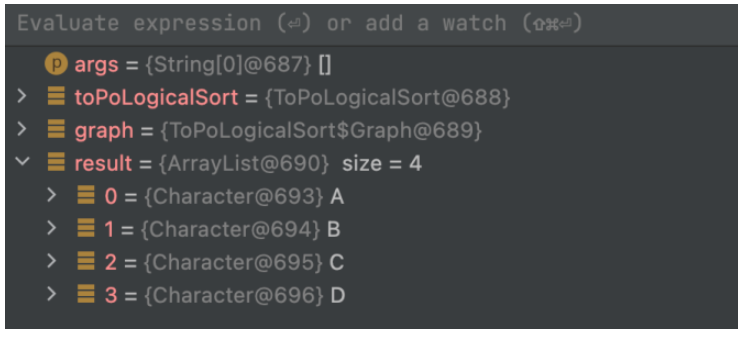
}実行結果
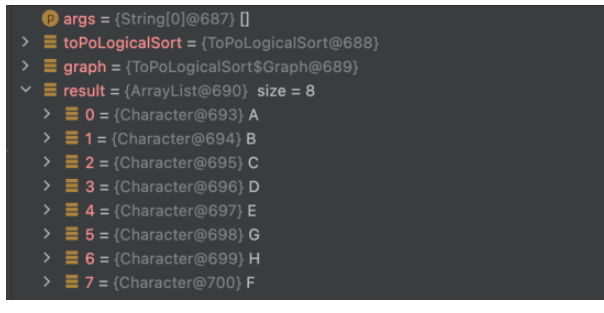
テストサンプル例2
public static void main(String[] args) {
ToPoLogicalSort toPoLogicalSort = new ToPoLogicalSort();
//初始化一个图
Graph graph = new Graph(new char[]{'A', 'B', 'C', 'D','E','F','G','H'});
graph.addEdge(0, 1);
graph.addEdge(0,2);
graph.addEdge(0,3);
graph.addEdge(1,4);
graph.addEdge(2,4);
graph.addEdge(3,4);
graph.addEdge(4,7);
graph.addEdge(4,6);
graph.addEdge(7,5);
graph.addEdge(6,7);
List<Character> result = toPoLogicalSort.toPoLogicalSort(graph);
}実行結果
 #
#
以上がJava でトポロジーソートを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

