Pythonでデシジョンツリー分類アルゴリズムを実装する方法

事前情報

1. デシジョンツリー

書き換えられた文: 教師あり学習では、一般的に使用される分類アルゴリズムは決定木です。これはサンプルのバッチに基づいており、各サンプルには一連の属性と対応する分類結果が含まれています。これらのサンプルを学習に使用すると、アルゴリズムは新しいデータを正しく分類できるデシジョン ツリーを生成できます

2. サンプル データ

14 人の既存ユーザーとその個人属性があると仮定します。特定の商品を購入するかどうかは次のとおりです。

##No.年齢収入範囲職種信用格付け購入決定01高い 不安定悪いNo02##高0304#05>40 低安定悪いはい06> 40低安定良好なし0730- 40低安定良いはい08中不安定悪いNo09 低安定悪いは10>40中安定悪いはい##1230-40中不安定良いはい1330-40高い安定悪い中##

Ce ツリー分類アルゴリズム

1. データセットの構築

処理を容易にするために、シミュレーション データは次の規則に従って数値リスト データに変換されます:

年齢: 40 には 2 の値が割り当てられます。

収入: 低は 0、中は 1、高はは 2

作業の性質: 不安定は 0、安定は 1

信用評価: 悪いは 0、良いは 1

#创建数据集
def createdataset():
    dataSet=[[0,2,0,0,'N'],
            [0,2,0,1,'N'],
            [1,2,0,0,'Y'],
            [2,1,0,0,'Y'],
            [2,0,1,0,'Y'],
            [2,0,1,1,'N'],
            [1,0,1,1,'Y'],
            [0,1,0,0,'N'],
            [0,0,1,0,'Y'],
            [2,1,1,0,'Y'],
            [0,1,1,1,'Y'],
            [1,1,0,1,'Y'],
            [1,2,1,0,'Y'],
            [2,1,0,1,'N'],]
    labels=['age','income','job','credit']
    return dataSet,labels

関数を呼び出してデータを取得します:

ds1,lab = createdataset()
print(ds1)
print(lab)

#[[0, 2 , 0, 0, ‘N’], [0, 2, 0, 1, ‘N’], [1, 2, 0, 0, ‘Y’ ;], [2, 1, 0, 0, ‘Y’], [2, 0, 1, 0, ‘Y’], [2, 0, 1, 1, ‘N’], [1 、0、1、1、「Y」]、[0、1、0、0、「N」]、[0、0、1、0、「Y」]、[2、1、1、 0, "Y"]、[0, 1 , 1, 1, "Y"]、[1, 1, 0, 1, "Y"]、[1, 2, 1, 0, "Y" ;], [2, 1, 0, 1, ‘N’]]

[‘年齢’, ‘収入’, ‘job’, ‘credit’]

#2. データセット情報エントロピー

情報エントロピー (シャノン エントロピーとも呼ばれる) は、確率変数の期待値です。情報の不確実性の度合いを測定します。情報のエントロピーが大きくなるほど、情報を把握することが難しくなります。情報を加工するとは、情報を明確にすることであり、エントロピーを低減するプロセスである。

def calcShannonEnt(dataSet):
    numEntries = len(dataSet)
    labelCounts = {}
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        
        labelCounts[currentLabel] += 1            
        
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob*log(prob,2)
    
    return shannonEnt

サンプル データ情報エントロピー:

shan = calcShannonEnt(ds1)
print(shan)

0.9402859586706309

3. 情報ゲイン

情報ゲイン: 属性 A の測定に使用されます。サンプルセット X エントロピーの寄与を減らします。得られる情報が大きいほど、X の分類に適しています。

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0])-1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0;bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntroy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prop = len(subDataSet)/float(len(dataSet))
            newEntroy += prop * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntroy
        if(infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i    
    return bestFeature

上記のコードは、情報エントロピー ゲインに基づいた ID3 決定木学習アルゴリズムを実装しています。その中心となる論理原則は、属性セット内の各属性を順番に選択し、この属性の値に従ってサンプル セットをいくつかのサブセットに分割し、これらのサブセットの情報エントロピーと、そのサブセットの情報エントロピーとの差を計算することです。サンプルは、この属性セグメント化の情報エントロピー ゲインに基づいており、すべてのゲインの中で最大のゲインに対応する属性を見つけます。これは、サンプル セットをセグメント化するために使用される属性です。

サンプルの最適な分割サンプル属性を計算します。結果は年齢属性である列 0 に表示されます:

col = chooseBestFeatureToSplit(ds1)
col

0

# #4. 構築の決定 Tree

def majorityCnt(classList):
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys():classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classList.iteritems(),key=operator.itemgetter(1),reverse=True)#利用operator操作键值排序字典
    return sortedClassCount[0][0]

#创建树的函数    
def createTree(dataSet,labels):
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
        
    return myTree

majorityCnt

関数は、次の状況を処理するために使用されます: 最終的な理想的な決定ツリーが決定分岐に沿って最下位に到達する必要があるとき、すべてのサンプルは同じ分類結果です。ただし、実際のサンプルでは、​​すべての属性が一致しているにもかかわらず分類結果が異なることは避けられず、この場合、

majorityCnt は、そのようなサンプルの分類ラベルを最も出現回数の多い分類結果に調整します。 createTree

はコア タスク関数であり、すべての属性に対して ID3 情報エントロピー ゲイン アルゴリズムを順番に呼び出して計算および処理し、最終的に決定木を生成します。

5. インスタンス化によるデシジョン ツリーの構築

サンプル データを使用してデシジョン ツリーを構築します:

Tree = createTree(ds1, lab)
print("样本数据决策树：")
print(Tree)

サンプル データ デシジョン ツリー:

{‘年齢’: {0: {‘仕事’: {0: ‘N’, 1: ‘Y’}},

1: ‘Y’,

2: {‘クレジット’: {0: ‘Y’, 1: ‘N’}}}

6. テスト サンプルの分類

新しいものを与えるユーザーが特定の製品を購入するかどうかを決定するための情報:

##年齢

	不安定	良好	なし
30-40	高い	不安定	悪い	は
>40	中	不安定	悪い	はい
					##11
中	安定	良い	はい
		#は		14	>40
不安定	良い	いいえ

収入範囲##低#安定##良い良いresult1: N投稿情報: デシジョン ツリー コードの描画

仕事の内容	信用格付け
	#	高	不安定
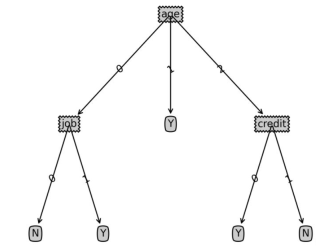
	def classify(inputtree,featlabels,testvec): firststr = list(inputtree.keys())[0] seconddict = inputtree[firststr] featindex = featlabels.index(firststr) for key in seconddict.keys(): if testvec[featindex]==key: if type(seconddict[key]).__name__=='dict': classlabel=classify(seconddict[key],featlabels,testvec) else: classlabel=seconddict[key] return classlabel labels=['age','income','job','credit'] tsvec=[0,0,1,1] print('result:',classify(Tree,labels,tsvec)) tsvec1=[0,2,0,1] print('result1:',classify(Tree,labels,tsvec1))	result: Y

次のコードは、デシジョン ツリー アルゴリズムの焦点では​​なく、デシジョン ツリー グラフィックを描画するために使用されます。興味があれば学習の参考にしてください

import matplotlib.pyplot as plt

decisionNode = dict(box, fc="0.8")
leafNode = dict(box, fc="0.8")
arrow_args = dict(arrow)

#获取叶节点的数目
def getNumLeafs(myTree):
    numLeafs = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':#测试节点的数据是否为字典，以此判断是否为叶节点
            numLeafs += getNumLeafs(secondDict[key])
        else:   numLeafs +=1
    return numLeafs

#获取树的层数
def getTreeDepth(myTree):
    maxDepth = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':#测试节点的数据是否为字典，以此判断是否为叶节点
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:   thisDepth = 1
        if thisDepth > maxDepth: maxDepth = thisDepth
    return maxDepth

#绘制节点
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeTxt, xy=parentPt,  xycoords='axes fraction',
             xytext=centerPt, textcoords='axes fraction',
             va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )

#绘制连接线  
def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
    yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)

#绘制树结构  
def plotTree(myTree, parentPt, nodeTxt):#if the first key tells you what feat was split on
    numLeafs = getNumLeafs(myTree)  #this determines the x width of this tree
    depth = getTreeDepth(myTree)
    firstStr = list(myTree.keys())[0]     #the text label for this node should be this
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
    plotMidText(cntrPt, parentPt, nodeTxt)
    plotNode(firstStr, cntrPt, parentPt, decisionNode)
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes   
            plotTree(secondDict[key],cntrPt,str(key))        #recursion
        else:   #it's a leaf node print the leaf node
            plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD

#创建决策树图形    
def createPlot(inTree):
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)    #no ticks
    #createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses 
    plotTree.totalW = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;
    plotTree(inTree, (0.5,1.0), '')
    plt.savefig('决策树.png',dpi=300,bbox_inches='tight')
    plt.show()

以上がPythonでデシジョンツリー分類アルゴリズムを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。