Python で @cache を使用する方法

#Python における @cache の魔法のような使い方とは何ですか?

キャッシュ戦略を採用すると、空間を時間に変換できるため、コンピューター システムのパフォーマンスが向上します。コード内のキャッシュの役割は、コードの実行速度を最適化することですが、メモリ フットプリントは増加します。

Python の組み込みモジュール functools では、デコレータとして使用されるキャッシュを実装するために高階関数 cache() が提供されています: @cache。

@cache キャッシュ関数の紹介

キャッシュのソースコードでは、キャッシュについて次のように説明されています: Simple Lightweight Unbounded Cache. 「memoize」とも呼ばれます. 中国語に翻訳すると: Simple Lightweight Unbounded Cache.キャッシュを制限します。 「メモ化」と呼ばれることもあります。

def cache(user_function, /):
    'Simple lightweight unbounded cache.  Sometimes called "memoize".'
    return lru_cache(maxsize=None)(user_function)

cache() のコードは 1 行だけで、lru_cache() 関数を呼び出し、パラメータ maxsize=None を渡します。 lru_cache() は functools モジュールの関数でもあります。lru_cache() のソース コードを確認してください。maxsize のデフォルト値は 128 です。これは、キャッシュされるデータの最大値が 128 であることを意味します。データが 128 を超える場合、データは次のように削除されます。 LRU (最長未使用) アルゴリズムのデータに変換します。 queue() が maxsize を None に設定すると、LRU 機能が無効になり、キャッシュの数が無限に増加する可能性があるため、「無制限キャッシュ」と呼ばれます。

lru_cache() は、長い間使用されていなかった LRU (Least Recent Used) アルゴリズムを使用しているため、関数名に 3 文字の lru が含まれています。最も使用されていないアルゴリズムのメカニズムは、データが最近アクセスされていないと仮定すると、将来アクセスされる可能性も非常に小さいということです。LRU アルゴリズムは、最も最近使用されていないデータを削除し、残っているデータを保持することを選択します。よく使われるデータです。

cache() は Python 3.9 バージョンの新機能、lru_cache() は Python 3.2 バージョンの新機能、cache() は lru_cache() に基づいてキャッシュ数の制限を解除します。技術の進歩とハードウェア パフォーマンスの大幅な向上に関連するキャッシュ() と lru_cache() は、同じ関数の異なるバージョンにすぎません。

lru_cache() は本質的に、関数にキャッシュ関数を提供するデコレータです。受信パラメータの maxsize グループをキャッシュし、次回同じパラメータで関数が呼び出されたときに前の結果を直接返します。高オーバーヘッドまたは高 I/O 関数の呼び出し時間。

@キャッシュ アプリケーション シナリオ

キャッシュには、静的 Web コンテンツのキャッシュなど、幅広いアプリケーション シナリオがあります。ユーザーが静的コンテンツにアクセスする関数に @cache デコレータを直接追加できます。ウェブページ。

一部の再帰コードでは、関数コードを実行するために同じパラメーターが繰り返し渡されます。キャッシュを使用すると、計算の繰り返しを回避し、コードの時間の複雑さを軽減できます。

次に、@cache の役割をフィボナッチ数列を例に挙げて説明しますが、前の内容がまだ少しでも理解できている方は、この例を読むと理解できると思います。

フィボナッチ数列とは、1、1、2、3、5、8、13、21、34、... の 3 番目の数字から始まる一連の数字を指します。各数字は次の合計です。最初の 2 つの数字。ほとんどの初心者はフィボナッチ数列のコードを書いたことがあるでしょう。その実装は難しくありません。Python のコードは非常に簡潔です。次のように:

def feibo(n):
    # 第0个数和第1个数为1
    a, b = 1, 1
    for _ in range(n):
        # 将b赋值给a,将a+b赋值给b,循环n次
        a, b = b, a+b
    return a

もちろん、フィボナッチ数列のコードを実装するには多くの方法があります (少なくとも 5 つまたは 6 つ)。@cache のアプリケーション シナリオを説明するために、この記事では再帰的手法を使用してフィボナッチ数列のコードを書きます。次のようになります。

def feibo_recur(n):
    if n < 0:
        return "n小于0无意义"
    # n为0或1时返回1（前两个数为1）
    if n == 0 or n == 1:
        return 1
    # 根据斐波那契数列的定义，其他情况递归返回前两个数之和
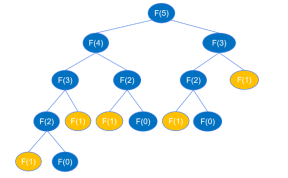
    return feibo_recur(n-1) + feibo_recur(n-2)

再帰コードが実行されると、次の図に示すように、feibo_recur(1) および feibo_recur(0) まで再帰されます (例として 6 番目の番号を使用します)。

F(5) を見つけるときは、まず F(4) と F(3) を見つけなければなりません。F(4) を見つけるときは、最初に F(3) を見つけなければなりません) および F( 2),... 類推すると、再帰プロセスはバイナリ ツリーの深さ優先のトラバースに似ています。高さ k の二分木は最大 2k-1 個のノードを持つことができることが知られています。上記の再帰呼び出し図によると、二分木の高さは n で、ノードは最大 2n-1 です。再帰関数呼び出しの回数は最大 2n-1 回であるため、再帰の時間計算量は O(2^n) です。

時間計算量が O(2^n) の場合、n が増加するにつれて実行時間は非常に大きく変化します。以下では実際にテストしてみましょう。

import time
for i in [10, 20, 30, 40]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)

出力:

10番目のフィボナッチ数: 89
n=10 コスト時間: 0.0
20番目のフィボナッチ数: 10946
n=20 コスト時間: 0.0015988349914550781
30 番目のフィボナッチ数: 1346269
n=30 コスト時間: 0.17051291465759277
40 番目のフィボナッチ数: 165580141
n=40 コスト時間: 20.90010976791382

実行時間を見ると、n が非常に小さい場合は実行時間が非常に速く、n が増加するにつれて実行時間は急激に増加し、特に n が 30、40 と徐々に増加すると、実行時間は特に顕著に変化します。時間変化パターンをより明確に確認するために、さらなるテストが行​​われました。

for i in [41, 42, 43]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)

出力:

41 番目のフィボナッチ数: 267914296
n=41 コスト時間: 33.77224683761597
42 番目のフィボナッチ数: 433494437
n=42 コスト時間: 55.86398696899414
43 番目のフィボナッチ数: 701408733
n=43 コスト時間: 92.55108690261841

从上面的变化可以看到，时间是指数级增长的（大约按1.65的指数增长），这跟时间复杂度为 O(2^n) 相符。按照这个时间复杂度，假如要计算第50个斐波那契数列，差不多要等一个小时，非常不合理，也说明递归的实现方式运算量过大，存在明显的不足。如何解决这种不足，降低运算量呢？接下来看如何进行优化。

根据前面的分析，递归代码运算量大，是因为递归执行时会不断的计算 feibo_recur(n-1) 和 feibo_recur(n-2)，如示例图中，要得到 feibo_recur(5) ，feibo_recur(1) 调用了5次。随着 n 的增大，调用次数呈指数级增长，导致出现大量的重复操作，浪费了许多时间。

假如有一个地方将每个 n 的执行结果记录下来，当作“备忘录”，下次函数再接收到这个相同的参数时，直接从备忘录中获取结果，而不用去执行递归的过程，就可以避免这些重复调用。在 Python 中，可以创建一个字典或列表来当作“备忘录”使用。

temp = {}  # 创建一个空字典，用来记录第i个斐波那契数列的值
def feibo_recur_temp(n):
    if n < 0:
        return "n小于0无意义"
    # n为0或1时返回1（前两个数为1）
    if n == 0 or n == 1:
        return 1
    if n in temp:  # 如果temp字典中有n,则直接返回值,不调用递归代码
        return temp[n]
    else:
        # 如果字典中还没有第n个斐波那契数，则递归计算并保存到字典中
        temp[n] = feibo_recur_temp(n-1) + feibo_recur_temp(n-2)
        return temp[n]

上面的代码中，创建了一个空字典用于存放每个 n 的执行结果。每次调用函数，都先查看字典中是否有记录，如果有记录就直接返回，没有记录就递归执行并将结果记录到字典中，再从字典中返回结果。这里的递归其实都只执行了一次计算，并没有真正的递归，如第一次传入 n 等于 5，执行 feibo_recur_temp(5)，会递归执行 n 等于 4, 3, 2, 1, 0 的情况，每个 n 计算过一次后 temp 中都有了记录，后面都是直接到 temp 中取数相加。每个 n 都是从temp中取 n-1 和 n-2 的值来相加，执行一次计算，所以时间复杂度是 O(n) 。

下面看一下代码的运行时间。

for i in [10, 20, 30, 40, 41, 42, 43]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur_temp(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)
print(temp)

Output:

第10个斐波那契数: 89
n=10 Cost Time:  0.0
第20个斐波那契数: 10946
n=20 Cost Time:  0.0
第30个斐波那契数: 1346269
n=30 Cost Time:  0.0
第40个斐波那契数: 165580141
n=40 Cost Time:  0.0
第41个斐波那契数: 267914296
n=41 Cost Time:  0.0
第42个斐波那契数: 433494437
n=42 Cost Time:  0.0
第43个斐波那契数: 701408733
n=43 Cost Time:  0.0
{2: 2, 3: 3, 4: 5, 5: 8, 6: 13, 7: 21, 8: 34, 9: 55, 10: 89, 11: 144, 12: 233, 13: 377, 14: 610, 15: 987, 16: 1597, 17: 2584, 18: 4181, 19: 6765, 20: 10946, 21: 17711, 22: 28657, 23: 46368, 24: 75025, 25: 121393, 26: 196418, 27: 317811, 28: 514229, 29: 832040, 30: 1346269, 31: 2178309, 32: 3524578, 33: 5702887, 34: 9227465, 35: 14930352, 36: 24157817, 37: 39088169, 38: 63245986, 39: 102334155, 40: 165580141, 41: 267914296, 42: 433494437, 43: 701408733}

可以观察到，代码的运行时间已经减少到小数点后很多位了（时间过短，只显示了0.0）。然而，temp 字典存储了每个数字的斐波那契数，这需要使用额外的内存空间，以换取更高的时间效率。

上面的代码也可以用列表来当“备忘录”，代码如下。

temp = [1, 1]
def feibo_recur_temp(n):
    if n < 0:
        return "n小于0无意义"
    if n == 0 or n == 1:
        return 1
    if n < len(temp):
        return temp[n]
    else:
        # 第一次执行时，将结果保存到列表中，后续直接从列表中取
        temp.append(feibo_recur_temp(n-1) + feibo_recur_temp(n-2))
        return temp[n]

现在，已经剖析了递归代码重复执行带来的时间复杂度问题，也给出了优化时间复杂度的方法，让我们将注意力转回到本文介绍的 @cache 装饰器。@cache 装饰器的作用是将函数的执行结果缓存，在下次以相同参数调用函数时直接返回上一次的结果，与上面的优化方式完全一致。

所以，只需要在递归函数上加 @cache 装饰器，递归的重复执行就可以解决，时间复杂度就能从 O(2^n) 降为 O(n) 。代码如下：

from functools import cache
@cache
def feibo_recur(n):
    if n < 0:
        return "n小于0无意义"
    if n == 0 or n == 1:
        return 1
    return feibo_recur(n-1) + feibo_recur(n-2)

使用 @cache 装饰器，可以让代码更简洁优雅，并且让你专注于处理业务逻辑，而不需要自己实现缓存。下面看一下实际的运行时间。

for i in [10, 20, 30, 40, 41, 42, 43]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)

Output:

第10个斐波那契数: 89
n=10 Cost Time:  0.0
第20个斐波那契数: 10946
n=20 Cost Time:  0.0
第30个斐波那契数: 1346269
n=30 Cost Time:  0.0
第40个斐波那契数: 165580141
n=40 Cost Time:  0.0
第41个斐波那契数: 267914296
n=41 Cost Time:  0.0
第42个斐波那契数: 433494437
n=42 Cost Time:  0.0
第43个斐波那契数: 701408733
n=43 Cost Time:  0.0

完美地解决了问题，所有运行时间都被精确到了小数点后数位（即使只显示 0.0），非常巧妙。若今后遇到类似情形，可以直接采用 @cache 实现缓存功能，通过“记忆化”处理。

补充：Python @cache装饰器

@cache和@lru_cache(maxsize=None)可以用来寄存函数对已处理参数的结果，以便遇到相同参数可以直接给出答案。前者无限制存储数量，而后者通过设定maxsize限制存储数量的上限。

例：

@lru_cache(maxsize=None) # 等价于@cache
def test(a,b):
    print('开始计算a+b的值...')
    return a + b

可以用来做某些递归、动态规划。比如斐波那契数列的各项值从小到大输出。其实类似用数组保存前项的结果，都需要额外的空间。不过用装饰器可以省略额外空间代码，减少了出错的风险。

以上がPython で @cache を使用する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。