Pythonをベースに単眼3D再構成を実現する方法

#1. 単眼 3 次元再構成の概要

対象世界の物体は 3 次元ですが、得られる画像は 2 次元ですが、この二次元画像から対象物の三次元情報をセンシングします。三次元再構成技術は、画像を何らかの方法で処理してコンピュータが認識できる三次元情報を取得し、対象物を解析する技術です。単眼 3D 再構成は、単一のカメラの動きに基づいて両眼視をシミュレートし、空間内のオブジェクトの 3 次元視覚情報を取得します。ここで、単眼とは単一のカメラを指します。

2. 実装プロセス

オブジェクトの単眼 3 次元再構築プロセスでは、関連する動作環境は次のとおりです:

matplotlib 3.3.4
numpy 1.19.5
opencv-contrib-python 3.4.2.16
opencv-python 3.4.2.16
pillow 8.2.0
python 3.6.2

再構成には主に以下の手順が含まれます。

#(1) カメラキャリブレーション

#(2) 画像特徴抽出とマッチング

#(3) 3 次元再構成

次に、各ステップの具体的な実装を詳しく見てみましょう:

(1) カメラのキャリブレーション

携帯電話のカメラなど、私たちの日常生活には多くのカメラがあります。デジタルカメラと機能モジュールの種類 カメラなど 各カメラのパラメータ、つまり、カメラで撮影される写真の解像度やモードなどが異なります。オブジェクトの 3 次元再構成を実行するときに、カメラの行列パラメータが事前にわからないと仮定すると、カメラの行列パラメータを計算する必要があります。この手順はカメラ キャリブレーションと呼ばれます。カメラのキャリブレーションに関する原理については、インターネット上の多くの方が詳しく説明しているので、ここでは紹介しません。キャリブレーションの具体的な実装は次のとおりです。

def camera_calibration(ImagePath):
    # 循环中断
    criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
    # 棋盘格尺寸（棋盘格的交叉点的个数）
    row = 11
    column = 8
    
    objpoint = np.zeros((row * column, 3), np.float32)
    objpoint[:, :2] = np.mgrid[0:row, 0:column].T.reshape(-1, 2)

    objpoints = []  # 3d point in real world space
    imgpoints = []  # 2d points in image plane.

    batch_images = glob.glob(ImagePath + '/*.jpg')
    for i, fname in enumerate(batch_images):
        img = cv2.imread(batch_images[i])
        imgGray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
        # find chess board corners
        ret, corners = cv2.findChessboardCorners(imgGray, (row, column), None)
        # if found, add object points, image points (after refining them)
        if ret:
            objpoints.append(objpoint)
            corners2 = cv2.cornerSubPix(imgGray, corners, (11, 11), (-1, -1), criteria)
            imgpoints.append(corners2)
            # Draw and display the corners
            img = cv2.drawChessboardCorners(img, (row, column), corners2, ret)
            cv2.imwrite('Checkerboard_Image/Temp_JPG/Temp_' + str(i) + '.jpg', img)

    print("成功提取:", len(batch_images), "张图片角点！")
    ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, imgGray.shape[::-1], None, None)

このうち、cv2.calibrateCamera 関数で取得した mtx 行列が K 行列です。

対応するパラメータを変更し、キャリブレーションを完了した後、チェッカーボードのコーナー ポイントの画像を出力して、チェッカーボードのコーナー ポイントが正常に抽出されたかどうかを確認できます。出力されるコーナー ポイントの画像は次のとおりです:

図 1: チェッカーボードの角点の抽出

(2) 画像特徴の抽出とマッチング

3 次元再構成プロセス全体では、このステップは最も重要であり、最も複雑なステップでもあり、画像特徴抽出の品質によって最終的な再構成効果が決まります。

画像特徴点抽出アルゴリズムには、SIFT アルゴリズム、SURF アルゴリズム、ORB アルゴリズムという 3 つのアルゴリズムがよく使われます。このステップでは、包括的な分析と比較を通じて、SURF アルゴリズムを使用して画像の特徴点を抽出します。 3 つのアルゴリズムの特徴点抽出効果を比較したい場合は、オンラインで検索して参照してください。ここでは 1 つずつの比較は行いません。具体的な実装は次のとおりです。

def epipolar_geometric(Images_Path, K):
    IMG = glob.glob(Images_Path)
    img1, img2 = cv2.imread(IMG[0]), cv2.imread(IMG[1])
    img1_gray = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)
    img2_gray = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)

    # Initiate SURF detector
    SURF = cv2.xfeatures2d_SURF.create()

    # compute keypoint & descriptions
    keypoint1, descriptor1 = SURF.detectAndCompute(img1_gray, None)
    keypoint2, descriptor2 = SURF.detectAndCompute(img2_gray, None)
    print("角点数量：", len(keypoint1), len(keypoint2))

    # Find point matches
    bf = cv2.BFMatcher(cv2.NORM_L2, crossCheck=True)
    matches = bf.match(descriptor1, descriptor2)
    print("匹配点数量：", len(matches))

    src_pts = np.asarray([keypoint1[m.queryIdx].pt for m in matches])
    dst_pts = np.asarray([keypoint2[m.trainIdx].pt for m in matches])
    # plot
    knn_image = cv2.drawMatches(img1_gray, keypoint1, img2_gray, keypoint2, matches[:-1], None, flags=2)
    image_ = Image.fromarray(np.uint8(knn_image))
    image_.save("MatchesImage.jpg")

    # Constrain matches to fit homography
    retval, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC, 100.0)

    # We select only inlier points
    points1 = src_pts[mask.ravel() == 1]
    points2 = dst_pts[mask.ravel() == 1]

見つかった特徴点は次のとおりです。

図 2: 特徴点の抽出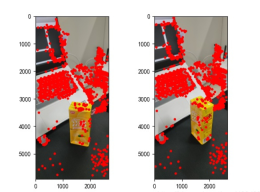

( 3) 3 次元再構成

画像の特徴点を見つけて相互に一致させたら、3 次元再構成を開始できます。具体的な実装は次のとおりです。再構成効果は次のとおりです (効果は平均です):

図 3: 3 次元再構成

#3. 結論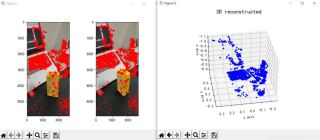

From再構成結果、単眼三次元再構成効果は平均的であるが、これらの点が関係しているのではないかと考えられる 関連要素：

(1) 撮影形態。単眼三次元再構成タスクの場合、写真を撮るときにカメラを平行に動かし続けるのが最善であり、正面から写真を撮るのが最善です。つまり、斜めまたは特別な角度で写真を撮らないでください。 ;

(2) 干渉撮影時の周囲環境。無関係な物体からの干渉を減らすために、単一の撮影場所を選択するのが最善です;

(3) 撮影光源の問題。選択した写真の場所では、適切な明るさを確保する必要があります (光源が基準を満たしているかどうかを確認するには、特定の状況をテストする必要があります)。また、カメラを移動するときは、直前の瞬間と今回の光源が一貫していることも確認する必要があります。一瞬。

実際のところ、単眼 3D 再構成のパフォーマンスは通常低く、すべての条件が最適な場合でも、得られる再構成効果はあまり良くありません。あるいは、両眼3D再構成を利用することも考えられますが、単眼よりも両眼3D再構成の方が確実に効果が高く、実装も少し面倒なだけです（笑）。実際、操作はそれほど複雑ではなく、2台のカメラの撮影とキャリブレーションが最も面倒で、その他の部分は比較的簡単です。

4.コード

points1 = cart2hom(points1.T)
points2 = cart2hom(points2.T)
# plot
fig, ax = plt.subplots(1, 2)
ax[0].autoscale_view('tight')
ax[0].imshow(cv2.cvtColor(img1, cv2.COLOR_BGR2RGB))
ax[0].plot(points1[0], points1[1], 'r.')
ax[1].autoscale_view('tight')
ax[1].imshow(cv2.cvtColor(img2, cv2.COLOR_BGR2RGB))
ax[1].plot(points2[0], points2[1], 'r.')
plt.savefig('MatchesPoints.jpg')
fig.show()
# 

points1n = np.dot(np.linalg.inv(K), points1)
points2n = np.dot(np.linalg.inv(K), points2)
E = compute_essential_normalized(points1n, points2n)
print('Computed essential matrix:', (-E / E[0][1]))

P1 = np.array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])
P2s = compute_P_from_essential(E)

ind = -1
for i, P2 in enumerate(P2s):
    # Find the correct camera parameters
    d1 = reconstruct_one_point(points1n[:, 0], points2n[:, 0], P1, P2)
    # Convert P2 from camera view to world view
    P2_homogenous = np.linalg.inv(np.vstack([P2, [0, 0, 0, 1]]))
    d2 = np.dot(P2_homogenous[:3, :4], d1)
    if d1[2] > 0 and d2[2] > 0:
        ind = i

P2 = np.linalg.inv(np.vstack([P2s[ind], [0, 0, 0, 1]]))[:3, :4]
Points3D = linear_triangulation(points1n, points2n, P1, P2)

fig = plt.figure()
fig.suptitle('3D reconstructed', fontsize=16)
ax = fig.gca(projection='3d')
ax.plot(Points3D[0], Points3D[1], Points3D[2], 'b.')
ax.set_xlabel('x axis')
ax.set_ylabel('y axis')
ax.set_zlabel('z axis')
ax.view_init(elev=135, azim=90)
plt.savefig('Reconstruction.jpg')
plt.show()

以上がPythonをベースに単眼3D再構成を実現する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。