Pythonを使用した取引戦略とポートフォリオ分析

この記事では、取引戦略のパフォーマンスを測定します。そして、債券、株式、不動産という 4 つの資産クラスを使用するシンプルなモメンタム取引戦略を開発します。これらの資産クラスは相関関係が低いため、優れたリスクバランスのオプションとなります。

モメンタム取引戦略

トレーダーや投資家はモメンタムの影響を長い間認識しているため、この戦略はモメンタムに基づいています。見られるように、幅広い市場と時間枠。したがって、私たちはそれをモメンタム戦略と呼びます。トレンドフォローまたはタイムシリーズモメンタム（TSM）は、単一の商品でこれらの戦略を使用することの別名です。基本的なモメンタム戦略を作成し、TCS でテストしてそのパフォーマンスを確認します。

TSM 戦略分析

まず、いくつかのライブラリをインポートします

import numpy as np
 import pandas as pd
 import matplotlib.pyplot as plt
 import yfinance as yf
 import ffn
 %matplotlib inline

基本的なモメンタム戦略関数 TSMStrategy を構築します。この関数は、時系列の対数リターン、対象期間、およびショートが許可されるかどうかのブール変数を介して、期待されるパフォーマンスを返します。

def TSMStrategy(returns, period=1, shorts=False):
if shorts:
position = returns.rolling(period).mean().map(
lambda x: -1 if x <= 0 else 1)
else:
position = returns.rolling(period).mean().map(
lambda x: 0 if x <= 0 else 1)
performance = position.shift(1) * returns
return performance
 ticker = 'TCS'
 yftcs = yf.Ticker(ticker)
 data = yftcs.history(start='2005-01-01', end='2021-12-31')
 returns = np.log(data['Close'] / data['Close'].shift(1)).dropna()
 performance = TSMStrategy(returns, period=1, shorts=False).dropna()
 years = (performance.index.max() - performance.index.min()).days / 365
 perf_cum = np.exp(performance.cumsum())
 tot = perf_cum[-1] - 1
 ann = perf_cum[-1] ** (1 / years) - 1
 vol = performance.std() * np.sqrt(252)
 rfr = 0.02
 sharpe = (ann - rfr) / vol
 print(f"1-day TSM Strategy yields:" +
f"nt{tot*100:.2f}% total returns" +
f"nt{ann*100:.2f}% annual returns" +
f"nt{sharpe:.2f} Sharpe Ratio")
 tcs_ret = np.exp(returns.cumsum())
 b_tot = tcs_ret[-1] - 1
 b_ann = tcs_ret[-1] ** (1 / years) - 1
 b_vol = returns.std() * np.sqrt(252)
 b_sharpe = (b_ann - rfr) / b_vol
 print(f"Baseline Buy-and-Hold Strategy yields:" +
f"nt{b_tot*100:.2f}% total returns" +
f"nt{b_ann*100:.2f}% annual returns" +
f"nt{b_sharpe:.2f} Sharpe Ratio")

関数の出力は次のとおりです。

1-day TSM Strategy yields:
 -45.15% total returns
 -7.10% annual returns
 -0.17 Sharpe Ratio
 Baseline Buy-and-Hold Strategy yields:
 -70.15% total returns
 -13.78% annual returns
 -0.22 Sharpe Ratio

妥当な年率リターンという観点から見ると、1 日 TSM 戦略はバイ アンド ホールド戦略よりも優れています。 1 日のルックバックには多くの誤った傾向が含まれる可能性があるため、異なる期間を試してそれらがどのように比較されるかを確認しました。ここでは、モデルは 3、5、15、30、90 日間ループで実行されます。

 import matplotlib.gridspec as gridspec
 periods = [3, 5, 15, 30, 90]
 fig = plt.figure(figsize=(12, 10))
 gs = fig.add_gridspec(4, 4)
 ax0 = fig.add_subplot(gs[:2, :4])
 ax1 = fig.add_subplot(gs[2:, :2])
 ax2 = fig.add_subplot(gs[2:, 2:])
 ax0.plot((np.exp(returns.cumsum()) - 1) * 100, label=ticker, linestyle='-')
 perf_dict = {'tot_ret': {'buy_and_hold': (np.exp(returns.sum()) - 1)}}
 perf_dict['ann_ret'] = {'buy_and_hold': b_ann}
 perf_dict['sharpe'] = {'buy_and_hold': b_sharpe}
 for p in periods:
log_perf = TSMStrategy(returns, period=p, shorts=False)
perf = np.exp(log_perf.cumsum())
perf_dict['tot_ret'][p] = (perf[-1] - 1)
ann = (perf[-1] ** (1/years) - 1)
perf_dict['ann_ret'][p] = ann
vol = log_perf.std() * np.sqrt(252)
perf_dict['sharpe'][p] = (ann - rfr) / vol
ax0.plot((perf - 1) * 100, label=f'{p}-Day Mean')
 
 ax0.set_ylabel('Returns (%)')
 ax0.set_xlabel('Date')
 ax0.set_title('Cumulative Returns')
 ax0.grid()
 ax0.legend()
 _ = [ax1.bar(i, v * 100) for i, v in enumerate(perf_dict['ann_ret'].values())]
 ax1.set_xticks([i for i, k in enumerate(perf_dict['ann_ret'])])
 ax1.set_xticklabels([f'{k}-Day Mean'
if type(k) is int else ticker for
k in perf_dict['ann_ret'].keys()],
rotation=45)
 ax1.grid()
 ax1.set_ylabel('Returns (%)')
 ax1.set_xlabel('Strategy')
 ax1.set_title('Annual Returns')
 _ = [ax2.bar(i, v) for i, v in enumerate(perf_dict['sharpe'].values())]
 ax2.set_xticks([i for i, k in enumerate(perf_dict['sharpe'])])
 ax2.set_xticklabels([f'{k}-Day Mean'
if type(k) is int else ticker for
k in perf_dict['sharpe'].keys()],
rotation=45)
 ax2.grid()
 ax2.set_ylabel('Sharpe Ratio')
 ax2.set_xlabel('Strategy')
 ax2.set_title('Sharpe Ratio')
 plt.tight_layout()
 plt.show()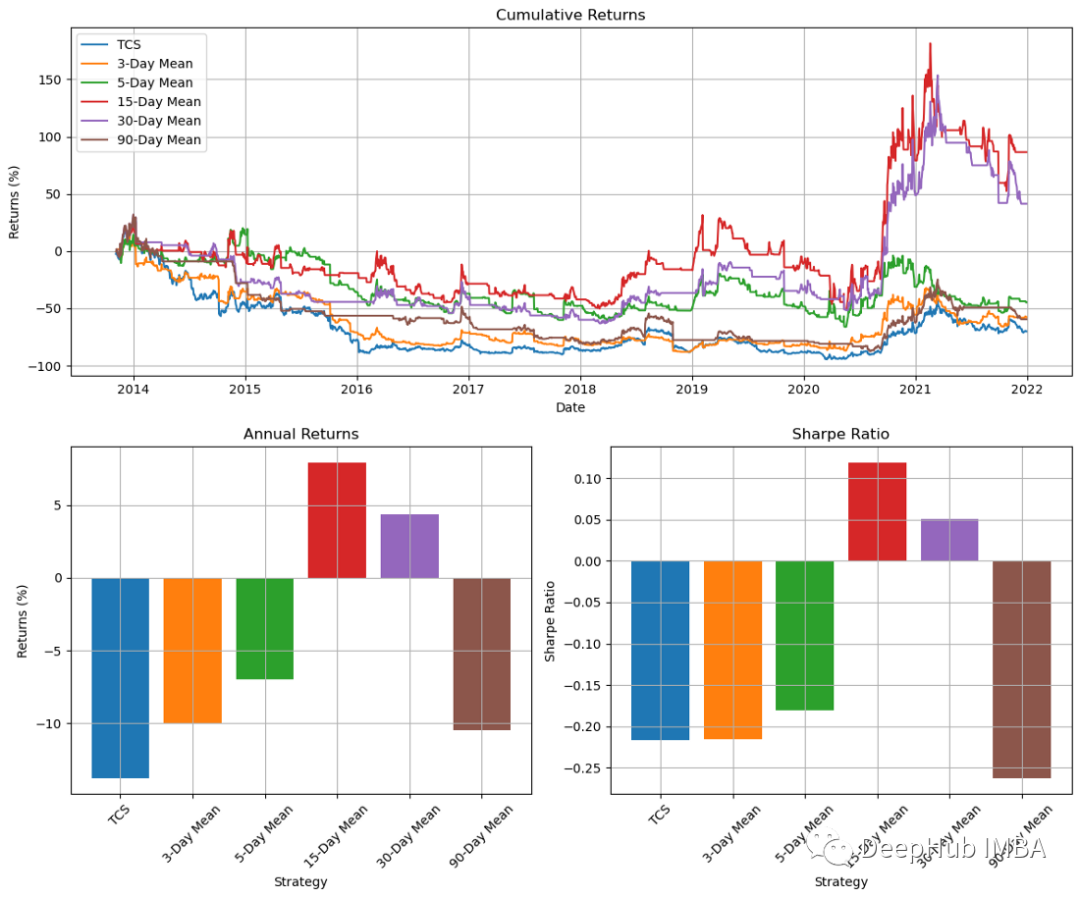

チャート上の結果を見ると、15 日間のモメンタム指標が最良の結果を提供していることがわかります。ただし、他の期間の結果はまちまちです。これは私たちの戦略が信頼できないことを示しています。したがって、15日チャートが下落または横ばいのときに取引を終了するのではなく、最高値付近でストップまたはトレーリングストップを使用して取引を終了することもできます。

ポートフォリオ分析

これまで、Python でトレーディング戦略を作成してきました。以下では、観察と分析を容易にするために、一般的なポートフォリオの特性を測定してプロットします。

ポートフォリオ分析

まず、いくつかの重要なライブラリをインポートし、データの実行を観察します。

import pandas_datareader.data as web
 stocks = ['SPY','GLD','TLT','HYG']
 
 data = web.DataReader(stocks,data_source='yahoo',start='01/01/2019')['Adj Close']
 data.sort_index(ascending=True,inplace=True)
 perf = data.calc_stats()
 perf.plot()

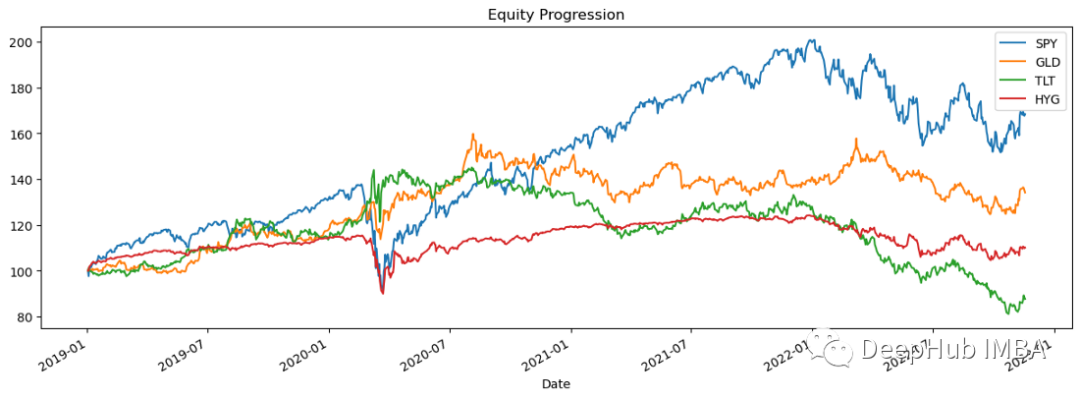
対数リターン

対数リターンは、指数関数的な成長率を計算するために使用されます。各サブ期間の価格変化の割合を計算する代わりに、その期間のオーガニック成長指数を計算します。まず、データ内の各株価の対数リターンを含む df を作成し、次に各対数リターンのヒストグラムを作成します。

 returns = data.to_log_returns().dropna()
 print(returns.head())
 
 
 Symbols SPY GLD TLT HYG
 Date
 2019-01-03 -0.024152 0.009025 0.011315 0.000494
 2019-01-04 0.032947 -0.008119 -0.011642 0.016644
 2019-01-07 0.007854 0.003453 -0.002953 0.009663
 2019-01-08 0.009351 -0.002712 -0.002631 0.006470
 2019-01-09 0.004663 0.006398 -0.001566 0.001193

ヒストグラムは次のとおりです:

ax = returns.hist(figsize=(20, 10),bins=30)

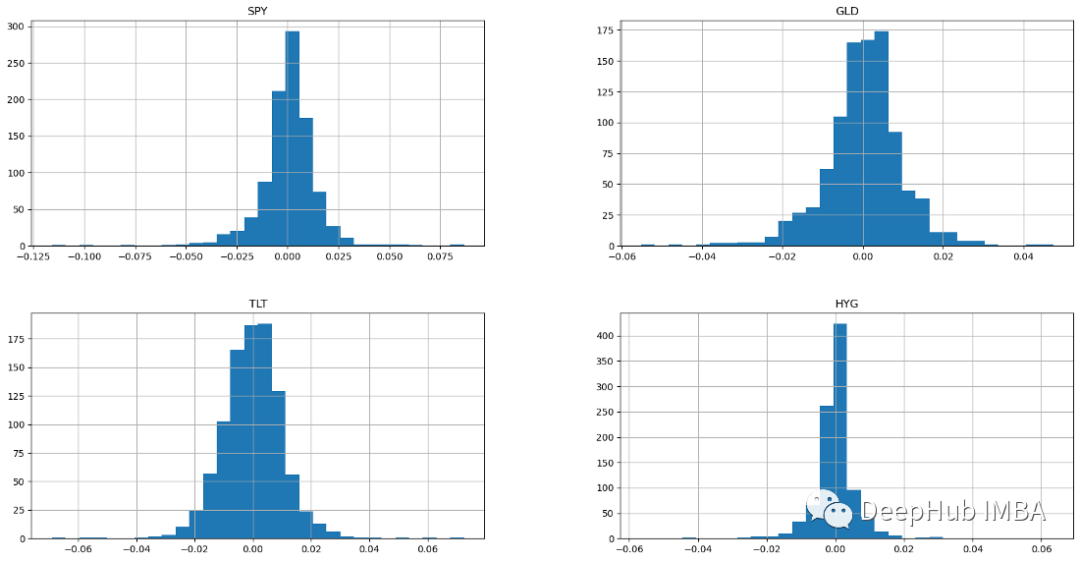
4 つの資産クラスすべての正規分布を示すヒストグラム。正規分布を持つサンプルには、算術平均と、平均の上下に等しい分布があります (ガウス分布とも呼ばれる正規分布は対称です)。リターンが正規分布する場合、リターンの 99% 以上が平均の 3 標準偏差以内に収まると予想されます。これらの釣鐘型の正規分布の特徴により、アナリストや投資家は株式の期待収益とリスクについてより適切な統計的推論を行うことができます。ベルカーブを持つ株は通常、ボラティリティが低く予測可能な優良銘柄です。

最大リトレースメント率 DRAWDOWN

DRAWDOWN とは、相対的に低い値に低下することを指します。これは投資家にとって考慮すべき重要なリスク要因です。減少戦略を視覚的に表現してみましょう。

ffn.to_drawdown_series(data).plot(figsize=(15,10))

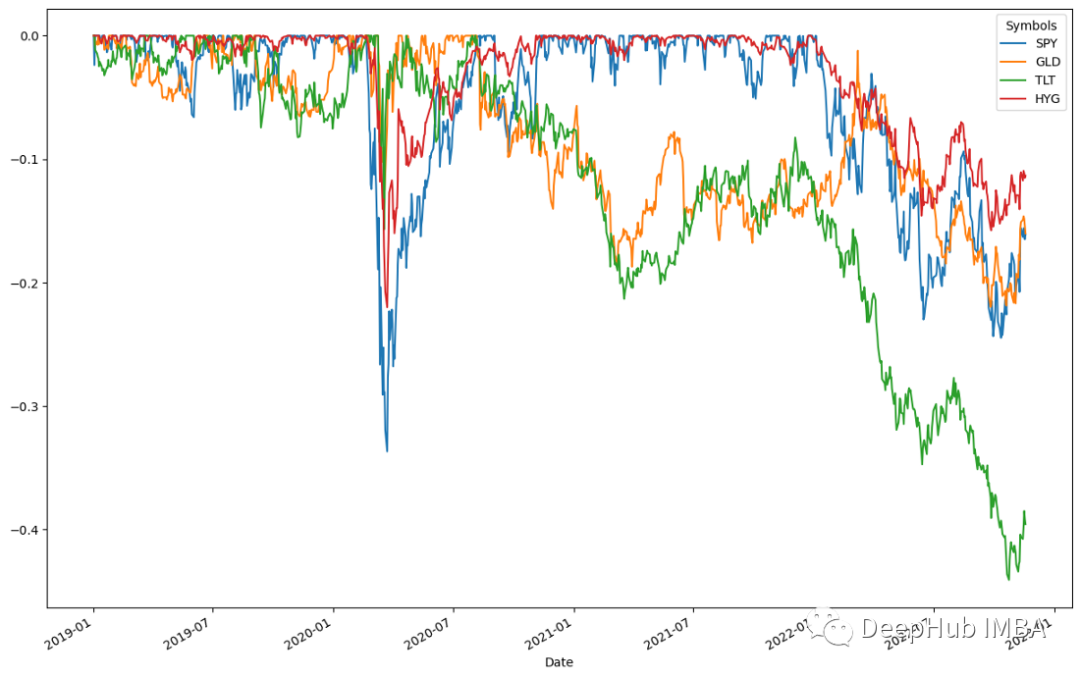
2020 年上半期には 4 つの資産すべてが下落し、SPY が 0.5% という最大の下落を経験しました。そして、2020年上半期にはすべての資産がすぐに回復しました。これは高い資産回収率を示しています。これらの資産は 2020 年 7 月頃にピークに達しました。この傾向に従い、回復がピークに達した後は、すべての資産クラスが小幅な下落を記録しました。この結果によると、TLTは2022年下半期に0.5％という最大の下落を経験し、その後2023年初めまでに回復すると予想されている。

マルコウィッツ平均分散最適化

1952 年、マルコウィッツ (MARKOWITZ) は、現代ポートフォリオ理論としても知られる平均分散ポートフォリオ理論を提案しました。投資家はこれらの概念を使用して、特定のレベルのリスクに基づいて期待収益を最大化するポートフォリオを構築できます。マーコウィッツ法に基づいて「最適なポートフォリオ」を生成することができます。

returns.calc_mean_var_weights().as_format('.2%')
 #结果
 SPY 46.60%
 GLD 53.40%
 TLT 0.00%
 HYG 0.00%
 dtype: object

相関統計

相関とは、証券間の関係を測定するために使用される統計手法です。この情報は、ヒート マップを使用して表示するのが最適です。ヒートマップを使用すると、証券間の相関関係を確認できます。

returns.plot_corr_heatmap()

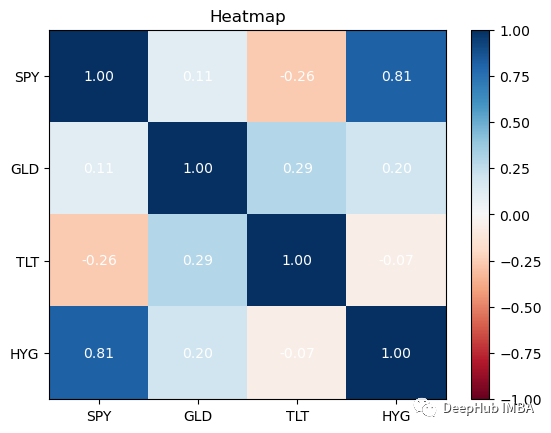
最好在你的投资组合中拥有相关性较低的资产。除了SPY与HYG，这四个资产类别的相关性都很低，这对我们的投资组合是不利的：因为如果拥有高度相关的不同资产组，即使你将风险分散在它们之间，从投资组合构建的角度来看，收益也会很少。

总结

通过分析和绘制的所有数据进行资产配置，可以建立一个投资组合，极大地改变基础投资的风险特征。还有很多我没有提到的，但可以帮助我们确定交易策略价值的起点。我们将在后续文章中添加更多的技术性能指标。

以上がPythonを使用した取引戦略とポートフォリオ分析の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。